Section #5: Drawing
Written by Nick Parlante and Elyse Cornwall
This week in section, you'll practice drawing. You can download the Pycharm project above to test your solutions to the coding problems.
Draw Diagonal
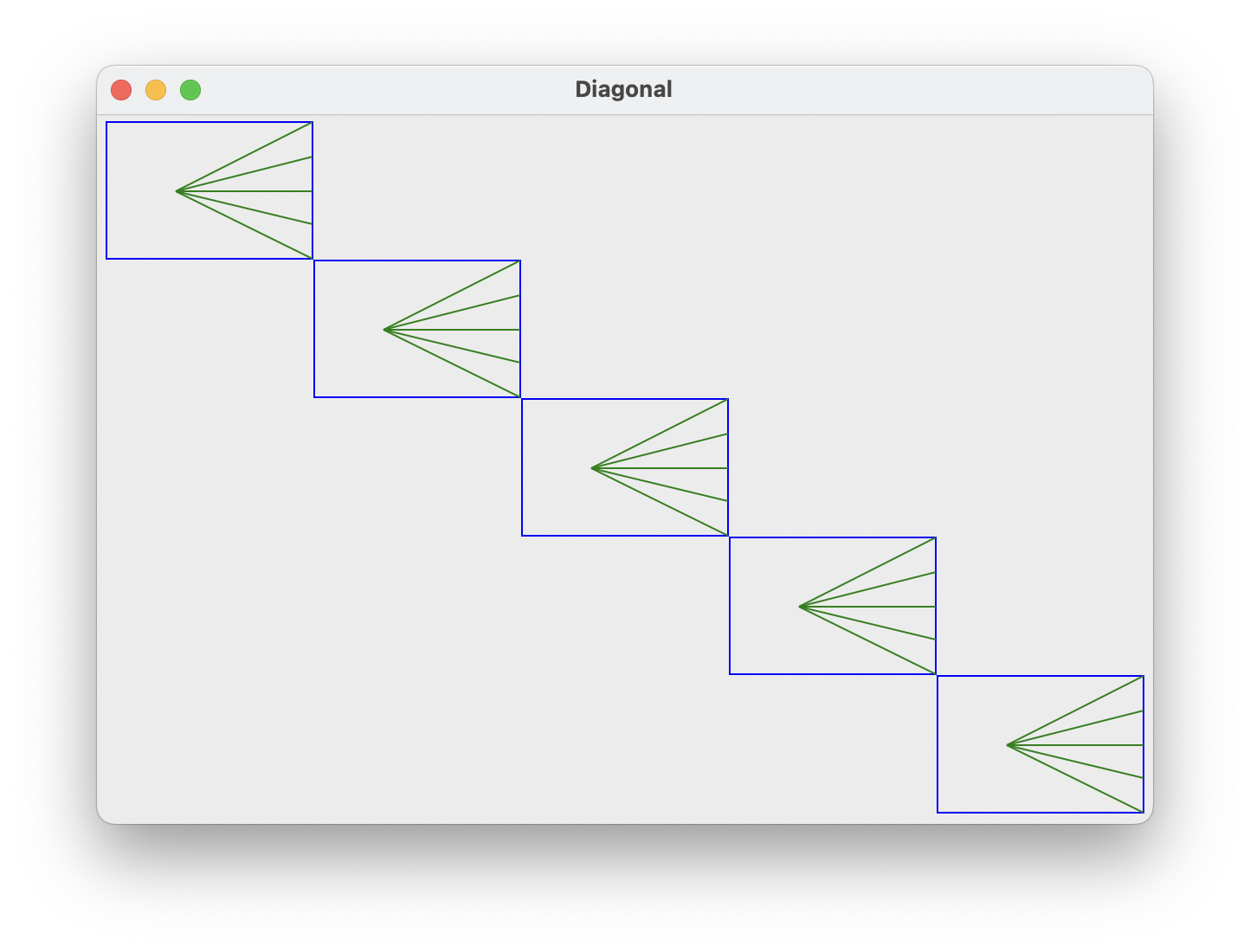
We'll write a program that can draw n diagonal copies of a "horn" figure across a canvas, as shown
below. Each horn consists of n lines drawn from one point on the figure to the right side of the
figure, spread from the top to the bottom.
"V" Figure Warmup
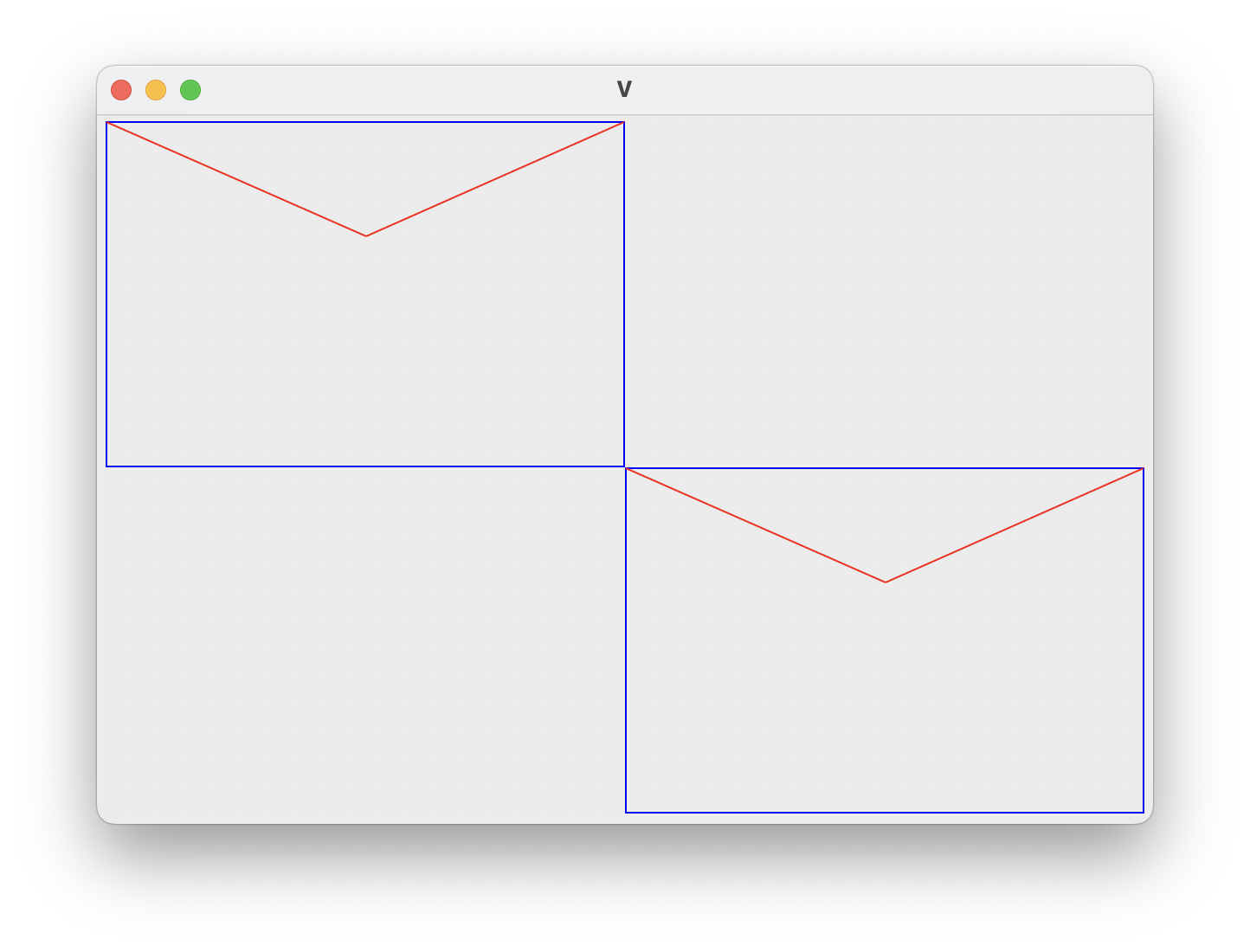
First, let's investigate some provided code to get a feel for drawing on a canvas. The function
draw_v(canvas, left, top, width, height) draws the "v" figure, two of which are shown
in the image below. Note that this is result of calling draw_v twice.
If you've downloaded the Pycharm project, try running the following commands in your terminal to see similar outputs:
python3 drawsection.py -v 600 400
python3 drawsection.py -v 600 100
python3 drawsection.py -v 1000 1000
Let's take a closer look at the parameters for this function. The width and height
specify the dimensions of the figure. The left and top specify the upper left
coordinate
of the figure. On each "v" figure, we have a
diagonal line from the upper left to the meeting point and from the upper right to the meeting point. We define
the
meeting point as halfway
across, and one-third of the way down the figure.
Before looking ahead to the code for draw_v, answer the following questions:
- Where do these diagonal lines start and end, based on the values we're given? Label the "v" figure with these coordinates.
- If we were drawing these lines with code, what would our function calls to
draw_linelook like?
def draw_v(canvas, left, top, width, height):
"""
Given a canvas and left,right and width,height.
Draw the "v" figure with that location and size.
"""
# Draw outer rectangle
canvas.draw_rect(left, top, width, height, color='blue')
# Mid is halfway across, 1/3 way down
mid_x = left + 0.5 * (width - 1)
mid_y = top + (1 / 3) * (height - 1)
# Draw lines from upper-left to mid, mid to upper-right
canvas.draw_line(left, top, mid_x, mid_y, color='red')
canvas.draw_line(mid_x, mid_y, left + width - 1, top, color='red')
Horn Figure
Now, you'll implement the function draw_horn(canvas, left, top, width, height, n) to draw the
horn figure. As shown before, a horn figure consists of n lines stretching from the meeting point
to
the right end of the figure, spread from the top to bottom right. Here, we define the
meeting point as one-third across, and halfway down the figure. The figure has dimensions
width, height and its upper left coordinate is (left, top).
Recall from lecture our strategy for positioning something some fraction (given by variable “frac”) of
the way across a figure: left + frac * (width - 1). How might we adapt this for the horn figure?
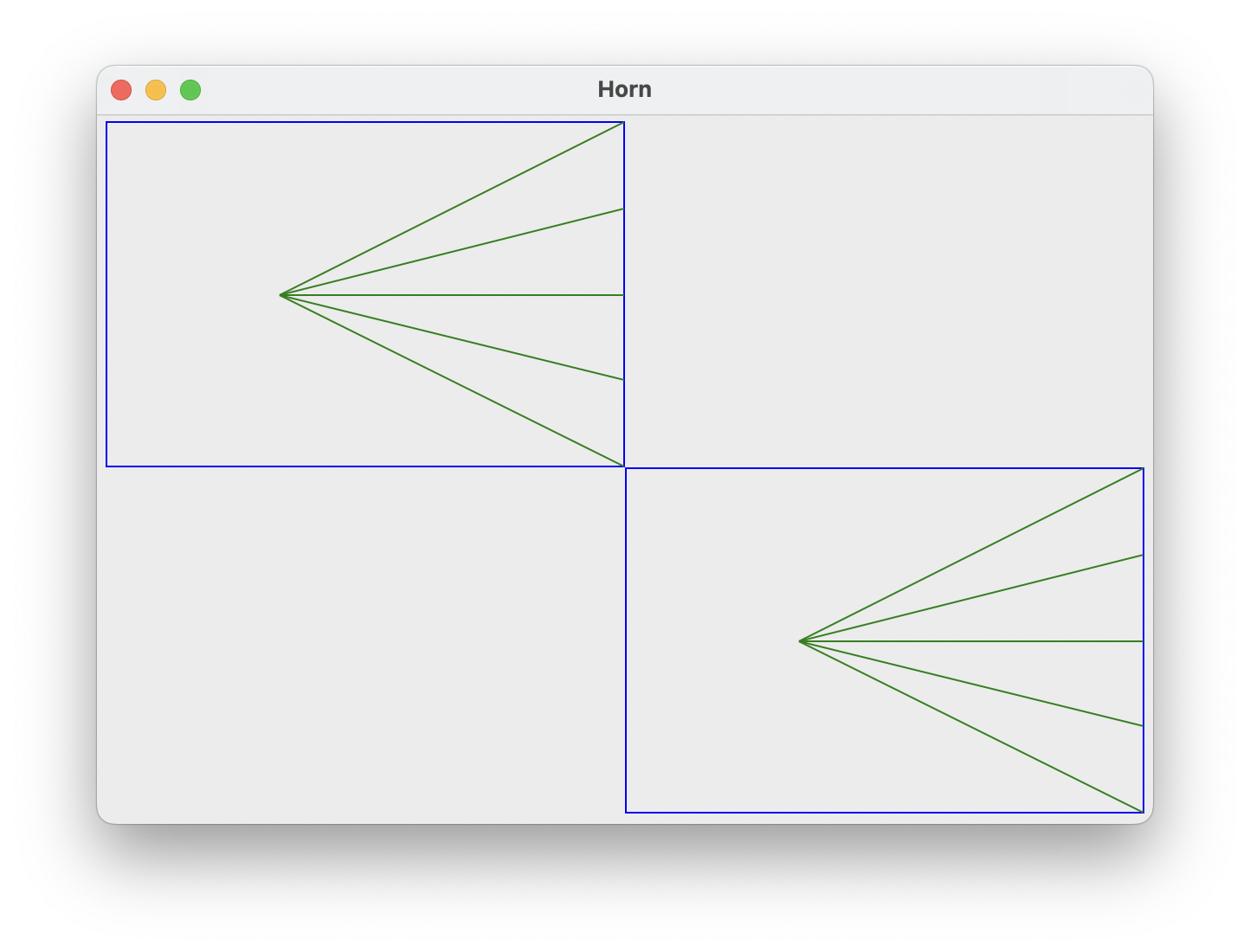
Test your code in the Pycharm project by running python3 drawsection.py -horn 600 400 5. You
should see two figures with five lines on each horn figure.
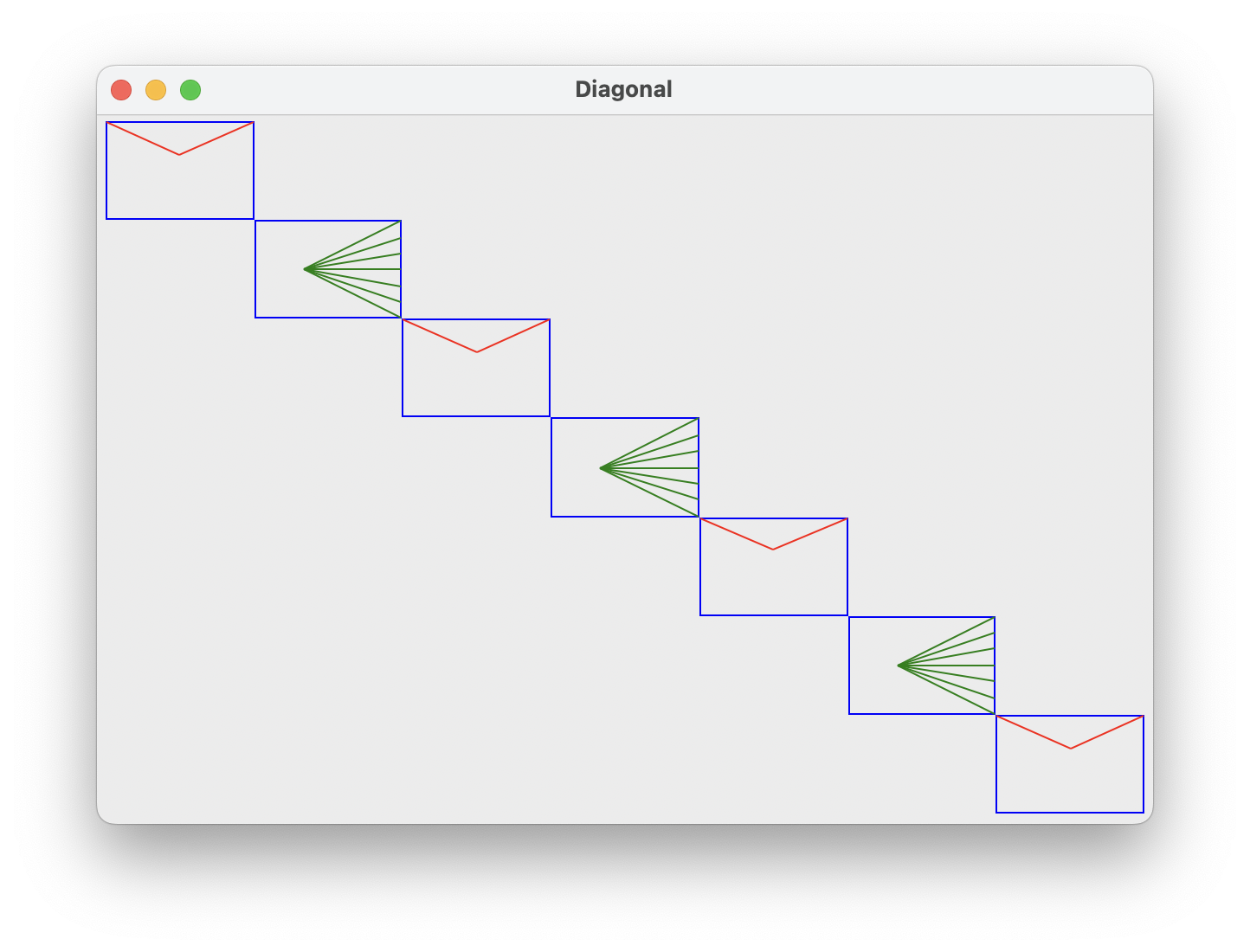
Draw Diagonal
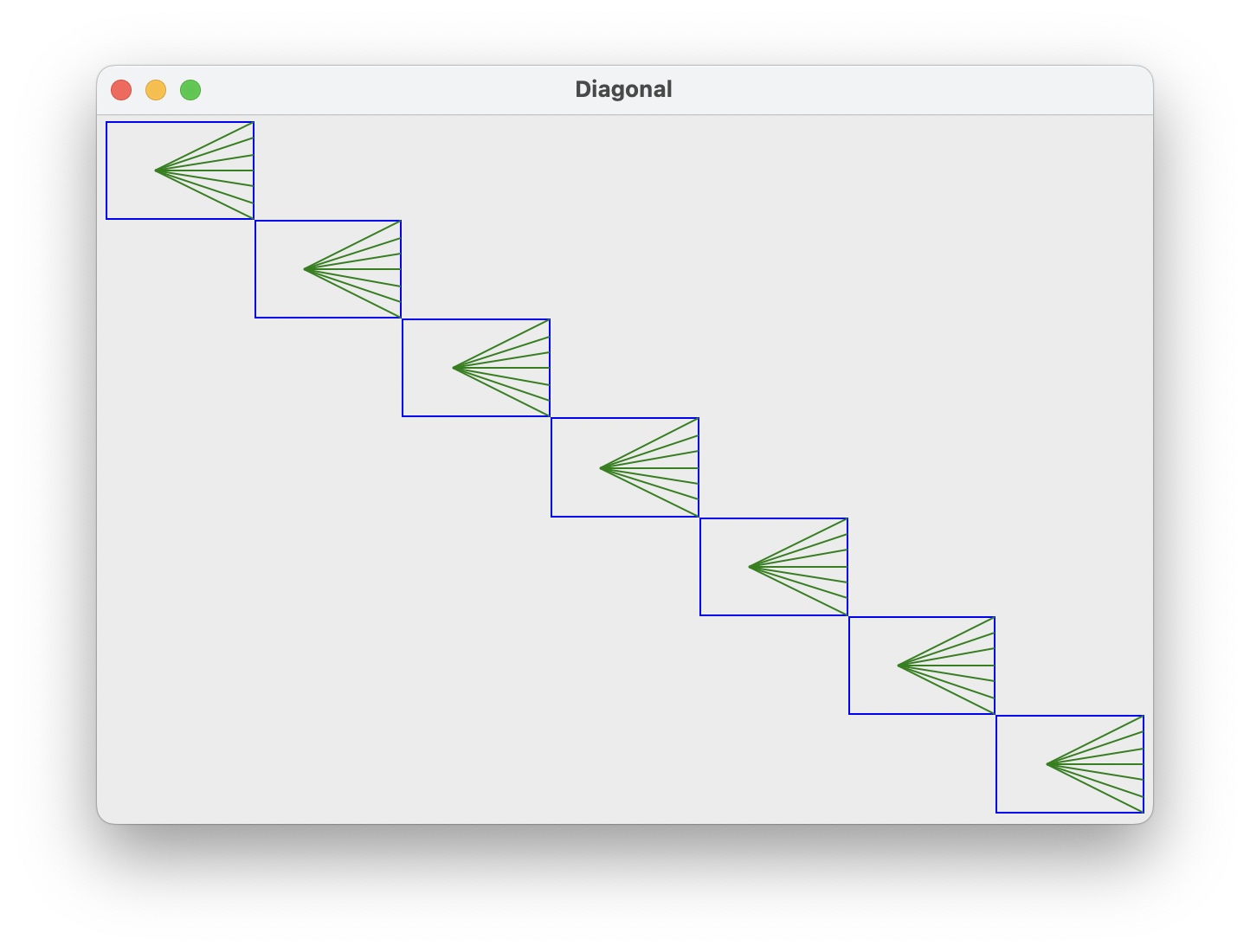
Finally, implement draw_diagonal(width, height, n), which draws n horn figures,
each with n lines, diagonally across a canvas with dimensions width, height. Below is
the result of calling draw_diagonal with n = 7.
Before you start coding, answer the following questions:
- What is the width and height of each figure, if the whole canvas has dimensions
width, height? - What is
left, topfor the first figure (in the upper left)? What about the second? Theith figure?
You can test your code by running python3 drawsection.py -diagonal 600 400 7 in the
terminal.
Draw Diagonal, Bonus
As a bonus, try modifying draw_diagonal to draw alternating horn and "v" figures. If you're using
a for i in range loop, you should draw a "v" figure when i is even, and a horn when
i is odd.
After modifying draw_diagonal, you can test your code by running the same command as above:
python3 drawsection.py -diagonal 600 400 7 in the
terminal.