Today: nesting, new data type dict and the dict-count algorithm, something extra at end

Python dict - Hash Table - Fast

• Python "dict" type, a "dictionary"
• Stores key/value pairs
• Each value is stored under a key
• In CS generally known as a "hash table"
  Sounds like a real hacker thing
  CS106B - look at hash table implementation
• Dict is a bit advanced, compared to basic string/list
• Defining features of a dict:
• 1. Choose a key to file each value under, e.g. Sunet, or transaction date
• 2. Get and set each value under its key
• 3. The get/set operations are fast

For more details sees the chapter in the Guide: Dict

Dict Story - Trader Joes

Suppose you come home and this is the situation:

cat with empty chip bag

Trader Joes Checkout Scanner - Dict Example

Visualize the check-out at Trader Joes. You hear "beep" "beep" as the barcode for each item is scanned. Each item's barcode holds a UPC code string, like '0061-4207'. The register needs to lookup the current price for each item.

The price data is stored in a dictionary. There is a key for each UPC code. Each key has an associated value stored in the dictionary, and in this case the value is the current price for each UPC. Each time the register looks up another UPC key to the price, it makes a little beep.

The superpower of the dict is lookup — given a UPC code string, e.g. '0061-4207', lookup the value stored in the dict for that key instantly, in this case 4.99. It makes no difference if the UPC code is the first or last in the dict, the lookup of the UPC key is basically instant.

Dict Basics

• 1. Organize data around keys
• 2. For a key, store one associated value
  In drawing with an arrow: key -> value
• 3. Can look up a value by its key
• 4. Not alphabetical - keys are in a random order

Dict-1 - Set key:value into Dict

• Create empty dict: d = {}
• Set: d[key] = value
• e.g. d['a'] = 'alpha'
• Set creates that key entry in dict if needed
• Overwrites any previous value for that key
  i.e. Each key has one value
• Literal dict syntax key:value
  {'a': 'alpha', 'g': 'gamma', 'b': 'beta'}
  Key (colon) Value (comma)

>>> d = {}             # Start with empty dict {}
>>> d['a'] = 'alpha'   # Set key/value
>>> d['g'] = 'gamma'
>>> d['b'] = 'beta'
>>> # Now we have built the picture above
>>> # Python can input/output a dict using
>>> # the literal { .. } syntax.
>>> d
{'a': 'alpha', 'g': 'gamma', 'b': 'beta'}
>>>

Dict-2 - Get value out of Dict

• Get a value out of a dict by key
• Get: d[key] - returns the value for that key
• e.g. d['a'] returns 'alpha'
• Note square bracket [ ] used for both setting and getting:
  d['a'] = x - setting
  x = d['a'] - getting
• Handy: +=
  Does a get/set series on the value
  This will be a handy pattern
• e.g. d['a'] += '!!!'
  Equivalent to: d['a'] = d['a'] + '!!!'
  Adds '!!!' to end of that value

>>> s = d['g']         # Get by key
>>> s
'gamma'
>>> d['b']
'beta'
>>> d['a'] = 'apple'   # Overwrite 'a' key
>>> d['a']
'apple'
>>>
>>> # += modify str value
>>> d['a'] += '!!!'
>>> d['a']
'apple!!!'
>>>
>>> d
{'a': 'apple!!!', 'g': 'gamma', 'b': 'beta'}
>>>

Dict-3 - Get Error / "in" Test

• There is one big catch
• Problem: get d[key] only works if the key is in the dict
  If the key is not in the dict, get d[key] fails with KeyError
• Solution: use in to check if a key is in the dict
• Habit: when you see d[key] .. think if that key is good
• Pattern: before using a key to get a value, in-check the key
  Sort of the "guard" pattern again

>>> # Can initialize dict with literal
>>> d = {'a': 'alpha', 'g': 'gamma', 'b': 'beta'}
>>>
>>> val = d['x']         # Key not in -> Error
Error:KeyError('x',)
>>>
>>> 'a' in d             # "in" key tests
True
>>> 'x' in d
False
>>> 
>>> # "in" logic before square bracket
>>> if 'x' in d:
      val = d['x']
>>>

Dict Logic - Always With Key not Value

The get/set/in logic of the dict is always by key. The key for each key/value pair is how it is set and found. The value is actually just stored without being looked at, just so it can be retrieved later. In particular get/set/in logic does not use the value. See the last line below.

>>> d = {'a': 'alpha', 'g': 'gamma', 'b': 'beta'}
>>>
>>> d['a']          # key works
'alpha'
>>> 'g' in d
True
>>> 
>>> 'gamma' in d    # value doesn't work
False
>>>

Summary of Dict: Set, Get, in, It's fast

• 1. Set: d[key] = value
• 2. Get: x = d[key]
• 3. In check: key in d
• The dict logic is always by key, the value is just stored
• These are all fast even with millions of key/value pairs

Dict Meals Structure

The dictionary is like memory - put something in, later can retrieve it.

Problems below use a "meals" dict to remember what food was eaten under the keys 'breakfast', 'lunch', 'dinner'.

>>> meals = {}
>>> meals['breakfast'] = 'apple'
>>> meals['lunch'] = 'donut'
>>>
>>> # time passes, other lines run
>>>
>>> # what was lunch again?
>>> meals['lunch']
'donut'
>>> 
>>> # did I have breakfast and dinner yet?
>>> 'breakfast' in meals
True
>>> 'dinner' in meals
False
>>>

Basic Dict Code Examples - Meals

Look at the dict1 "meals" exercises on the experimental server

> dict1 meals exercises

With the "meals" examples, the keys are 'breakfast', 'lunch', 'dinner' and the values are like 'hot dot' and 'bagel'. A key like 'breakfast' may or may not be in the dict, so need to "in" check first. No loops in these.

Common Bug: in/not-in Logic - Before dict[key]

Often we want to pull a value out for a particular key:

# Want - something like this
val = d[key]

But there is always the risk — what if that key is not in the dict? In that case, trying to read d[key] will crash with KeyError. Therefore, the code often has an "in" check about that key before trying to read that key .

# Write it this way
if key in d:
    val = d[key]

1. Example early_apple()

> early_apple()

early_apple(meals): Return True if 'breakfast' or 'lunch' is 'apple', and False otherwise.

early_apple() Solution Code

def early_apple(meals):
    if 'breakfast' in meals:
        if meals['breakfast'] == 'apple':
            return True
    if 'lunch' in meals:
        if meals['lunch'] == 'apple':
            return True
    # Could use "and" instead of nested "if"
    return False

More practice:

> bad_start()

bad_start(meals): Return True if there is no 'breakfast' key in meals, or the value for 'breakfast' is 'candy'. Otherwise return False.

2. Example enkale()

> enkale()

enkale(meals): If the key 'dinner' is in the dict with the value 'candy', change the value to 'kale'. Otherwise leave the dict unchanged. Return the dict in all cases.

enkale() Solution Code

Demo: work out the code, see key error

Cannot access meals['dinner'] in the case that dinner is not in the dict, so need logic to avoid that case.

def enkale(meals):
    if 'dinner' in meals:
        if meals['dinner'] == 'candy':
            meals['dinner'] = 'kale'
    return meals

Instead of nested-if, could write it with "and" (either way of writing it is fine):

def enkale(meals):
    if 'dinner' in meals and meals['dinner'] == 'candy':
        meals['dinner'] = 'kale'
    return meals

This is the "guard" pattern again — the "in" check guards the meals['dinner'] access, since the and/short-circuit goes left-to-right, and stops on a False.

Exercise: is_boring()

> is_boring()

is_boring(meals): Given a "meals" dict. We'll say the meals dict is boring if lunch and dinner are both present and are the same food. Return True if the meals dict is boring, False otherwise.

Idea: could solve without worrying about the KeyError first. Then put in the needed "in" guard checks.

Dict-Count Algorithm

• Extremely important dict algorithm pattern
  We'll use it a lot
  You will need to memorize it
  It's just a few lines
• A "counts" dict:
  We have some big data set
  Store a key for each distinct value in the data
  The value for each key is the count of occurrences of that key in the data

Example input strings:
  ['a', 'b', 'a', 'c', 'b']

Compute counts:
  {'a': 2, 'b': 2, 'c': 1}

Dict Count Code Examples

> dict2 Count exercises

Dict-Count Algorithm Steps

Do the following for each s in strs. At the end, counts dict is built.

• 1. Start with empty dict counts = {}
• 2. For each s test: not seen before?
• 3. Not seen before: store key = s, value = 1
• 4. Else seen before: key = s, value = value + 1

Dict-Count abacb

Go through these strs
strs = ['a', 'b', 'a',  'c',  'b']

Sketch out counts dict here:

Counts dict ends up as {'a': 2, 'b': 2, 'c': 1}:

• strs: 'a', 'b', 'a', 'c', 'b'
• Each distinct s is a key in the dict
• The value for each key is the number of times it is seen
• Algorithm: loop through all s, update dict with counts as we go
• Each s: not seen before?

1. str-count1() - if/else

> str_count1()

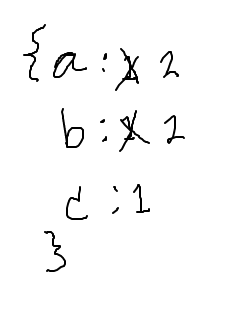
str_count1 demo, canonical dict-count algorithm

• Central test of this algorithm: not seen before?
• if/else solution
• Test: not seen before?
  not seen before: counts[s] = 1
  seen before: counts[s] += 1
• This if/else approach is fine, but we'll see another way below
• Demo: write code on board, then fix in next step

str_count1() Solution

def str_count1(strs):
    counts = {}
    for s in strs:
        # s not seen before?
        if s not in counts:
            counts[s] = 1   # first time
        else:
            counts[s] +=1   # every later time
    return counts

2. str-count2() - Unified/Invariant Version, no else

> str_count2()

• A slight unified/invariant improvement on the above code
• Explain from bottom up
• Instead of += only for existing inputs do it for every input unconditionally
• counts[s] += 1
• Problem: above will crash first time s appears, since it's not in there. Think about what the += expands to:
  e.g. counts[s] = counts[s] + 1
• Add this fix before:
• If s not seen before - set to zero - aka "fix" dict for that s
  if s not in counts: counts[s] = 0
• Now all counting goes through that one += 1 line
• I have a slight preference this version
  It's one fewer lines and does not use else

Standard Dict-Count Code - Unified/Invariant Version

def str_count2(strs):
    counts = {}
    for s in strs:
        # fix counts/s if not seen before
        if s not in counts:
            counts[s] = 0
        # Unified: now s is in counts one way or
        # another, so this works for all cases:
        counts[s] += 1
    return counts

Exercise - Int Count

> int_count()

Apply the dict-count algorithm to a list of int values, return a counts dict, counting how many times each int value appears in the list.

(optional) Char Count

May get to this one, or students do on their own.

> char_count()

Apply the dict-count algorithm to chars in a string. Build a counts dict of how many times each char, converted to lowercase, appears in a string so 'Coffee' returns {'c': 1, 'o': 1, 'f': 2, 'e': 2}.