Regression trees
Contents
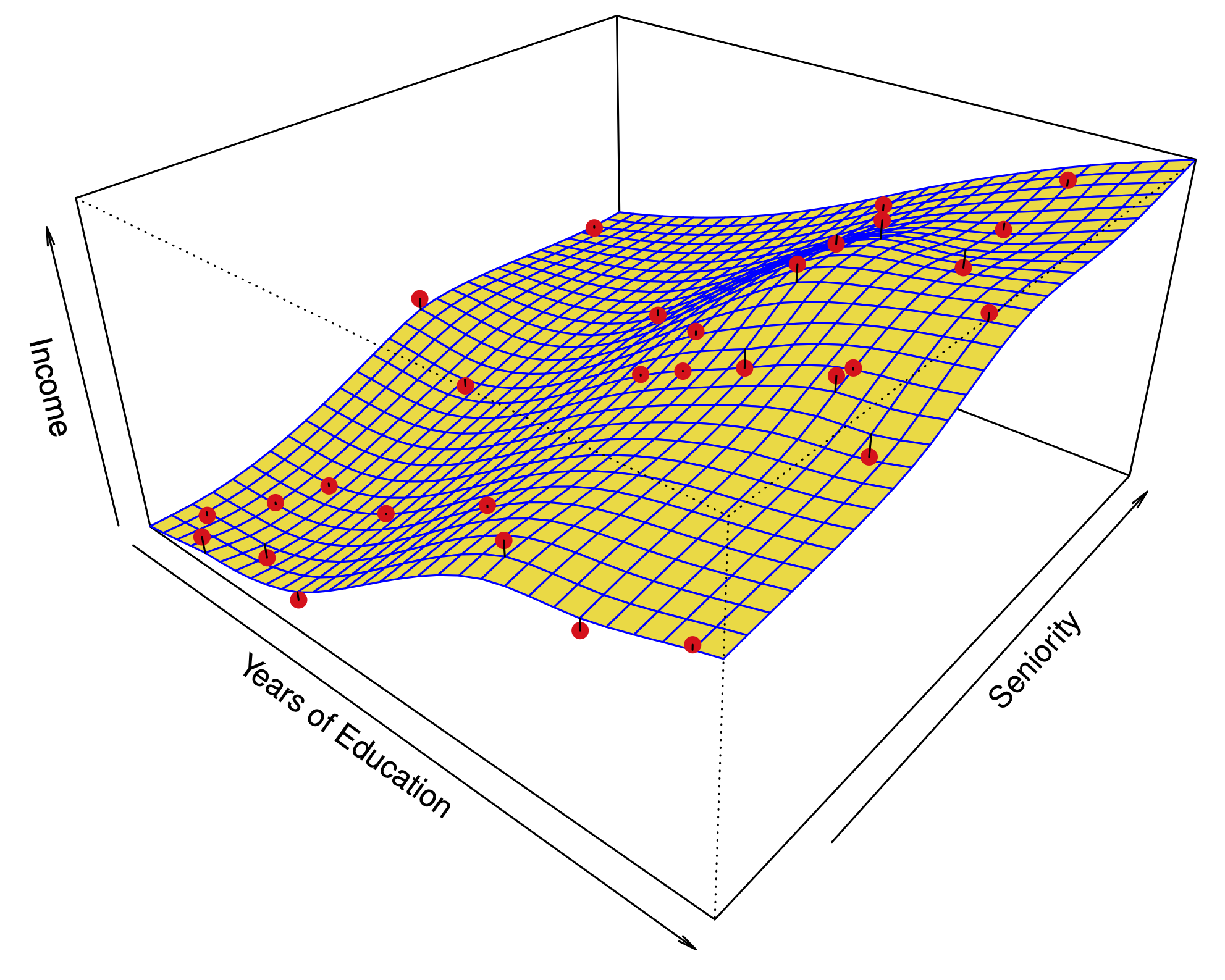
Regression trees#
Overview#

Find a partition of the space of predictors.
Predict a constant in each set of the partition.
The partition is defined by splitting the range of one predictor at a time.
Note: \(\to\) not all partitions are possible.
Example: Predicting a baseball player’s salary#
Fig 8.1 |
Fig 8.2 |
|---|---|

|

|
The prediction for a point in \(R_i\) is the average of the training points in \(R_i\).
How is a regression tree built?#
Start with a single region \(R_1\), and iterate:
Select a region \(R_k\), a predictor \(X_j\), and a splitting point \(s\), such that splitting \(R_k\) with the criterion \(X_j<s\) produces the largest decrease in RSS: $\(\sum_{m=1}^{|T|} \sum_{x_i\in R_m} (y_i-\bar y_{R_m})^2\)$
Redefine the regions with this additional split.
Terminate when there are, say, 5 observations or fewer in each region.
This grows the tree from the root towards the leaves.
How do we control overfitting?#

Idea 1: Find the optimal subtree by cross validation.
Hmm…. there are too many possibilities – harder than best subsets!
Idea 2: Stop growing the tree when the RSS doesn’t drop by more than a threshold with any new cut.
Hmm… in our greedy algorithm, it is possible to find good cuts after bad ones.
Solution: Prune a large tree from the leaves to the root.
Weakest link pruning:
Starting with \(T_0\), substitute a subtree with a leaf to obtain \(T_1\), by minimizing: $\(\frac{RSS(T_1)-RSS(T_0)}{|T_0|- |T_1|}.\)$
Iterate this pruning to obtain a sequence \(T_0,T_1,T_2,\dots,T_m\) where \(T_m\) is the null tree.
The sequence of trees can be used to solve the minimization for cost complexity pruning (over subtrees \(T \subset T_0\))
Choose \(\alpha\) by cross validation.
Example: predicting baseball salaries#

Optimally tuned tree#