Local linear regression
Contents
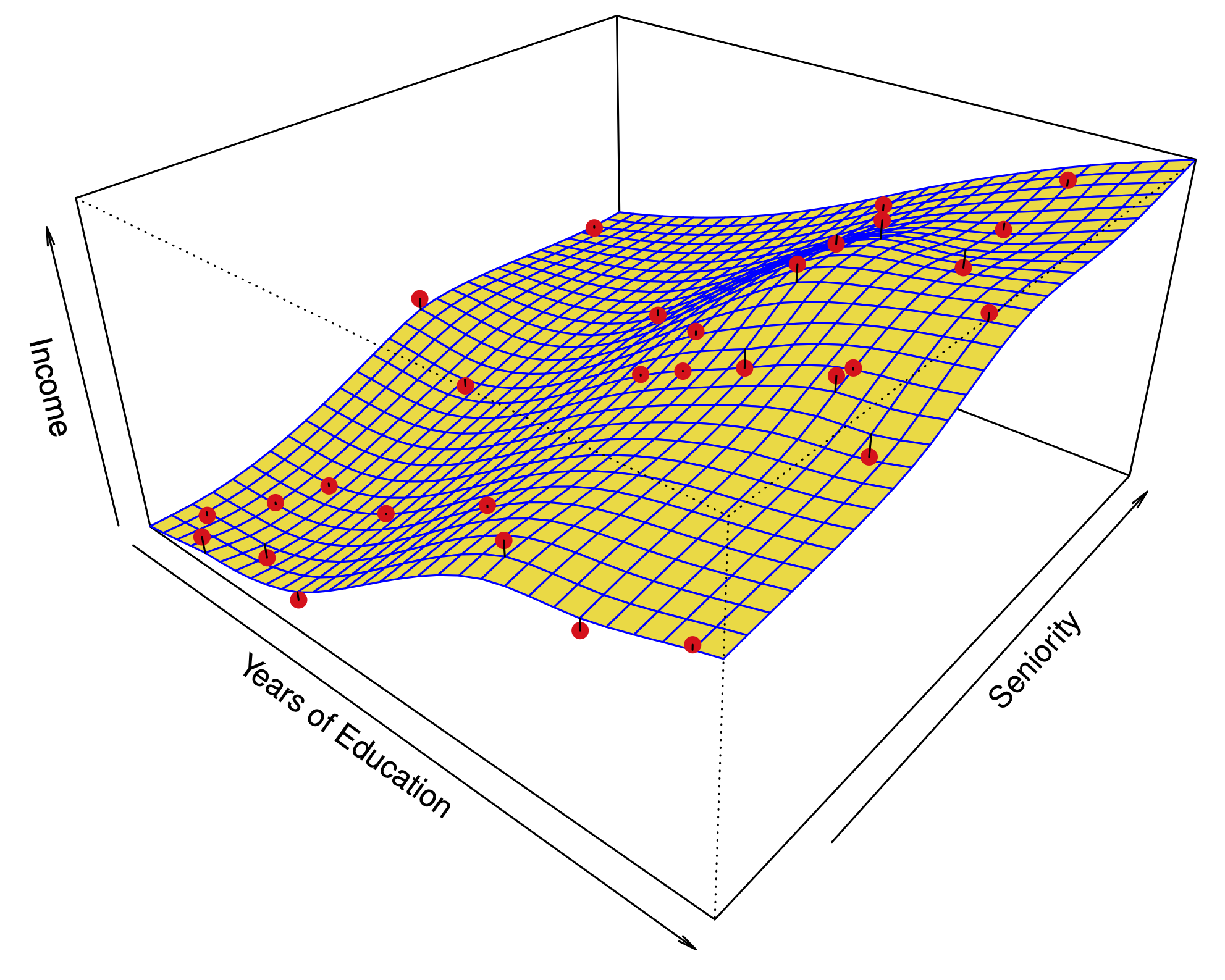
Local linear regression#

Sample points nearer \(x\) are weighted higher in corresponding regression.
Algorithm#
To predict the regression function \(f\) at an input \(x\):
Assign a weight \(K_i(x)\) to the training point \(x_i\), such that:
\(K_i(x)=0\) unless \(x_i\) is one of the \(k\) nearest neighbors of \(x\) (not strictly necessary).
\(K_i(x)\) decreases when the distance \(d(x,x_i)\) increases.
Perform a weighted least squares regression; i.e. find \((\beta_0,\beta_1)\) which minimize
Predict \(\hat f(x) = \hat \beta_0(x) + \hat \beta_1(x) x\).
Generalized nearest neighbors#
Set \(K_i(x)=1\) if \(x_i\) is one of \(x\)’s \(k\) nearest neighbors.
Perform a regression with only an intercept; i.e. find \(\beta_0\) which minimizes
Predict \(\hat f(x) = \hat \beta_0(x)\).
Gaussian (radial basis function) kernel#
Common choice that is smoother than nearest neighbors
Local linear regression#

The span \(k/n\), is chosen by cross-validation.