Linear Discriminant Analysis (LDA)#

  • Strategy: Instead of estimating \(P(Y\mid X)\) directly, we could estimate:

    1. \(\hat P(X \mid Y)\): Given the response, what is the distribution of the inputs.

    2. \(\hat P(Y)\): How likely are each of the categories.

  • Then, we use Bayes rule to obtain the estimate:

\[\begin{split} \begin{aligned} \hat P(Y = k \mid X = x) &= \frac{\hat P(X = x \mid Y = k) \hat P(Y = k)}{\hat P(X=x)} \\ &= \frac{\hat P(X = x \mid Y = k) \hat P(Y = k)}{\sum_{j=1}^K\hat P(X = x \mid Y=j) \hat P(Y=j)} \end{aligned} \end{split}\]

LDA: multivariate normal with equal covariance#

  • LDA is the special case of the above strategy when \(P(X \mid Y=k) = N(\mu_k, \mathbf\Sigma)\).

  • That is, within each class the features have multivariate normal distribution with center depending on the class and common covariance \(\mathbf\Sigma\).

  • The probabilities \(P(Y=k)\) are estimated by the fraction of training samples of class \(k\).

Decision boundaries#

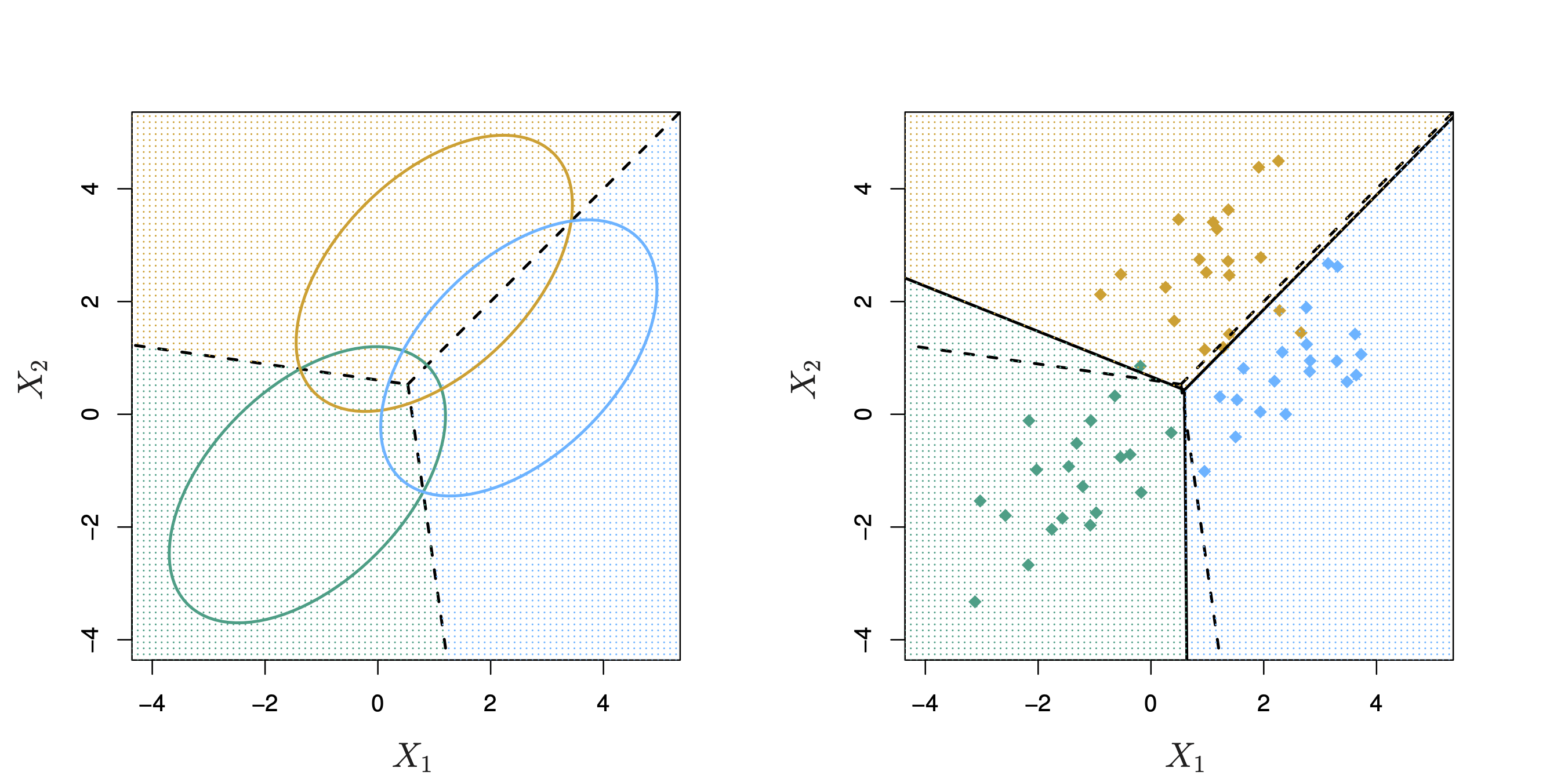
Fig 4.6

Fig. 17 Density contours and decision boundaries for LDA with three classes.#

LDA has (piecewise) linear decision boundaries#

Suppose that:

  1. We know \(P(Y=k) = \pi_k\) exactly.

  2. \(P(X=x | Y=k)\) is Mutivariate Normal with density:

\[f_k(x) = \frac{1}{(2\pi)^{p/2}|\mathbf\Sigma|^{1/2}} e^{-\frac{1}{2}(x-\mu_k)^T \mathbf{\Sigma}^{-1}(x-\mu_k)}\]

  1. Above: \(\mu_k:\) Mean of the inputs for category \(k\) and \(\mathbf\Sigma:\) covariance matrix (common to all categories)

Then, what is the Bayes classifier?

  • By Bayes rule, the probability of category \(k\), given the input \(x\) is:

\[P(Y=k \mid X=x) = \frac{f_k(x) \pi_k}{P(X=x)}\]

  • The denominator does not depend on the response \(k\), so we can write it as a constant:

\[P(Y=k \mid X=x) = C \times f_k(x) \pi_k\]

  • Now, expanding \(f_k(x)\):

\[P(Y=k \mid X=x) = \frac{C\pi_k}{(2\pi)^{p/2}|\mathbf\Sigma|^{1/2}} e^{-\frac{1}{2}(x-\mu_k)^T \mathbf{\Sigma}^{-1}(x-\mu_k)}\]

  • Let’s absorb everything that does not depend on \(k\) into a constant \(C'\):

\[P(Y=k \mid X=x) = C'\pi_k e^{-\frac{1}{2}(x-\mu_k)^T \mathbf{\Sigma}^{-1}(x-\mu_k)}\]

  • Take the logarithm of both sides: $\(\log P(Y=k \mid X=x) = \color{Red}{\log C'} + \color{blue}{\log \pi_k - \frac{1}{2}(x-\mu_k)^T \mathbf{\Sigma}^{-1}(x-\mu_k)}.\)$

  • This is the same for every category, \(k\).

  • We want to find the maximum of this expression over \(k\).

  • Goal is to maximize the following over \(k\): $\( \begin{aligned} &\log \pi_k - \frac{1}{2}(x-\mu_k)^T \mathbf{\Sigma}^{-1}(x-\mu_k).\\ =&\log \pi_k - \frac{1}{2}\left[x^T \mathbf{\Sigma}^{-1}x + \mu_k^T \mathbf{\Sigma}^{-1}\mu_k\right] + x^T \mathbf{\Sigma}^{-1}\mu_k \\ =& C'' + \log \pi_k - \frac{1}{2}\mu_k^T \mathbf{\Sigma}^{-1}\mu_k + x^T \mathbf{\Sigma}^{-1}\mu_k \end{aligned} \)$

  • We define the objectives (called discriminant functions): $\(\delta_k(x) = \log \pi_k - \frac{1}{2}\mu_k^T \mathbf{\Sigma}^{-1}\mu_k + x^T \mathbf{\Sigma}^{-1}\mu_k\)\( At an input \)x\(, we predict the response with the highest \)\delta_k(x)$.

Decision boundaries#

  • What are the decision boundaries? It is the set of points \(x\) in which 2 classes do just as well (i.e. the discriminant functions of the two classes agree at \(x\)):

\[\begin{split} \begin{aligned} \delta_k(x) &= \delta_\ell(x) \\ \log \pi_k - \frac{1}{2}\mu_k^T \mathbf{\Sigma}^{-1}\mu_k + x^T \mathbf{\Sigma}^{-1}\mu_k & = \log \pi_\ell - \frac{1}{2}\mu_\ell^T \mathbf{\Sigma}^{-1}\mu_\ell + x^T \mathbf{\Sigma}^{-1}\mu_\ell \end{aligned} \end{split}\]

  • This is a linear equation in \(x\).

Decision boundaries revisited#

Fig 4.6

Fig. 18 Density contours and decision boundaries for LDA with three classes.#

Estimating \(\pi_k\)#

\[\hat \pi_k = \frac{\#\{i\;;\;y_i=k\}}{n}\]

  • In English: the fraction of training samples of class \(k\).

Estimating the parameters of \(f_k(x)\)#

Estimate the center of each class \(\mu_k\):#

\[\hat\mu_k = \frac{1}{\#\{i\;;\;y_i=k\}}\sum_{i\;;\; y_i=k} x_i\]

  • Estimate the common covariance matrix \(\mathbf{\Sigma}\):

  • One predictor (\(p=1\)):

\[\hat \sigma^2 = \frac{1}{n-K}\sum_{k=1}^K \;\sum_{i:y_i=k} (x_i-\hat\mu_k)^2.\]

  • Many predictors (\(p>1\)): Compute the vectors of deviations \((x_1 -\hat \mu_{y_1}),(x_2 -\hat \mu_{y_2}),\dots,(x_n -\hat \mu_{y_n})\) and use an unbiased estimate of its covariance matrix, \(\mathbf\Sigma\).

Final decision rule#

  • For an input \(x\), predict the class with the largest:

\[\hat\delta_k(x) = \log \hat\pi_k - \frac{1}{2}\hat\mu_k^T \mathbf{\hat\Sigma}^{-1}\hat\mu_k + x^T \mathbf{\hat\Sigma}^{-1}\hat\mu_k\]

  • The decision boundaries are defined by \(\left\{x: \delta_k(x) = \delta_{\ell}(x) \right\}, 1 \leq j,\ell \leq K\).