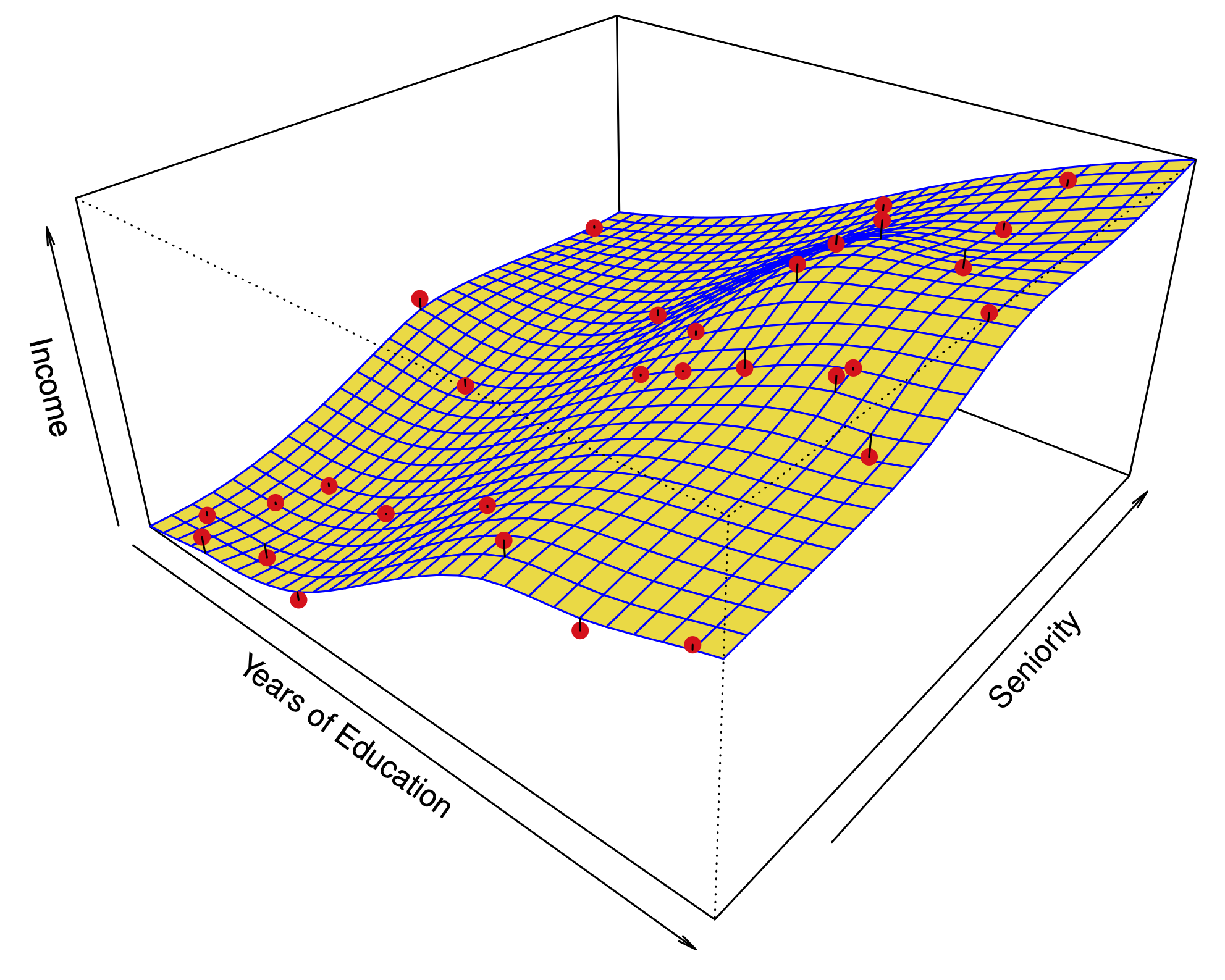
Simple linear regression#

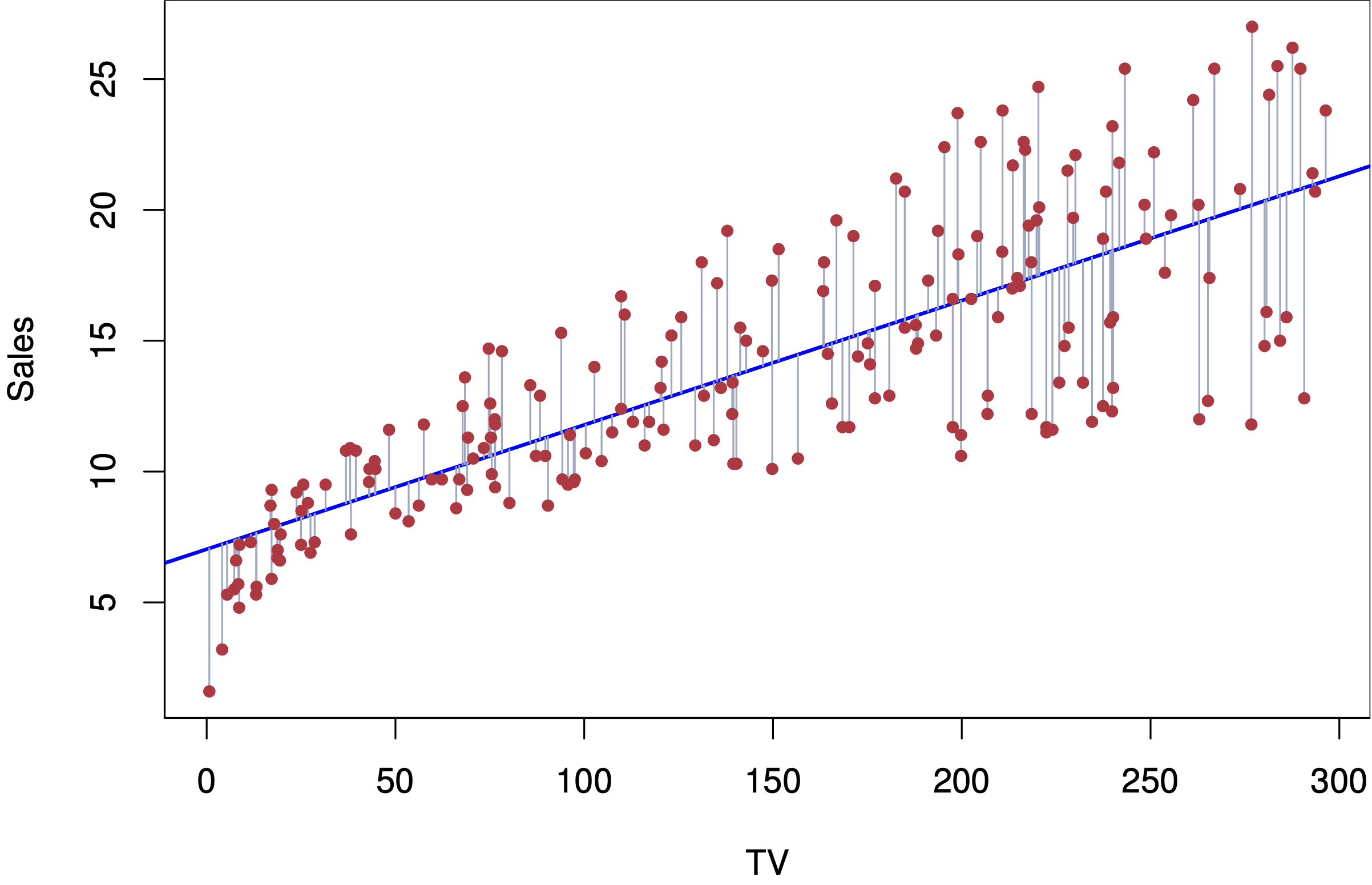
Fig 3.1

Fig. 9 Simple linear regression#

Model#

\[y_i = \beta_0 + \beta_1 x_i +\varepsilon_i\]

  • Errors: \(\varepsilon_i \sim N(0,\sigma^2)\quad \text{i.i.d.}\)

  • Fit: the estimates \(\hat\beta_0\) and \(\hat\beta_1\) are chosen to minimize the (training) residual sum of squares (RSS):

\[\begin{split} \begin{aligned} \text{RSS}(\beta_0,\beta_1) &= \sum_{i=1}^n (y_i -\hat y_i(\beta_0, \beta_1))^2 \\ & = \sum_{i=1}^n (y_i - \beta_0- \beta_1 x_i)^2. \end{aligned} \end{split}\]

Sample code: advertising data#

library(ISLR)
Advertising = read.csv("https://www.statlearning.com/s/Advertising.csv", header=TRUE, row.names=1)
M.sales = lm(sales ~ TV, data=Advertising)
M.sales

Estimates \(\hat\beta_0\) and \(\hat\beta_1\)#

A little calculus shows that the minimizers of the RSS are:

\[\begin{split} \begin{aligned} \hat \beta_1 & = \frac{\sum_{i=1}^n (x_i-\overline x)(y_i-\overline y)}{\sum_{i=1}^n (x_i-\overline x)^2} \\ \hat \beta_0 & = \overline y- \hat\beta_1\overline x. \end{aligned} \end{split}\]

Assessing the accuracy of \(\hat \beta_0\) and \(\hat\beta_1\)#

Fig 3.3

Fig. 10 How variable is the regression line?#

Based on our model#

  • The Standard Errors for the parameters are:

\[\begin{split} \begin{aligned} \text{SE}(\hat\beta_0)^2 &= \sigma^2\left[\frac{1}{n}+\frac{\overline x^2}{\sum_{i=1}^n(x_i-\overline x)^2}\right] \\ \text{SE}(\hat\beta_1)^2 &= \frac{\sigma^2}{\sum_{i=1}^n(x_i-\overline x)^2}. \end{aligned}\end{split}\]

  • 95% confidence intervals:

\[\begin{split} \begin{aligned} \hat\beta_0 &\pm 2\cdot\text{SE}(\hat\beta_0) \\ \hat\beta_1 &\pm 2\cdot\text{SE}(\hat\beta_1) \end{aligned} \end{split}\]

Hypothesis test#

  • Null hypothesis \(H_0\): There is no relationship between \(X\) and \(Y\).

  • Alternative hypothesis \(H_a\): There is some relationship between \(X\) and \(Y\).

  • Based on our model: this translates to

    • \(H_0\): \(\beta_1=0\).

    • \(H_a\): \(\beta_1\neq 0\).

  • Test statistic:

\[\quad t = \frac{\hat\beta_1 -0}{\text{SE}(\hat\beta_1)}.\]

  • Under the null hypothesis, this has a \(t\)-distribution with \(n-2\) degrees of freedom.

Sample output: advertising data#

summary(M.sales)
confint(M.sales)

Interpreting the hypothesis test#

  • If we reject the null hypothesis, can we assume there is an exact linear relationship?

  • No. A quadratic relationship may be a better fit, for example. This test assumes the simple linear regression model is correct which precludes a quadratic relationship.

  • If we don’t reject the null hypothesis, can we assume there is no relationship between \(X\) and \(Y\)?

  • No. This test is based on the model we posited above and is only powerful against certain monotone alternatives. There could be more complex non-linear relationships.