Landau-Ginzburg Theory
Onwards we continue in our quest for understanding complicated interacting systems! Last week, we built up our understanding of mean field theory, and this week, we'll extend the theory a bit further, thinking about how magnetization can vary throughout space, and working towards the concept of an order parameter field.
Overview
In my notes, we're going to take a slightly different approach than in class.
Rather than jumping right into the Landau-Ginzburg functional ![F[phi(vec{r})]](eqs/4356449759178279700-130.png) , we're going to go step by step to properly build up our intuition. Here's the game plan:
, we're going to go step by step to properly build up our intuition. Here's the game plan:
We want to understand what ![F[phi(vec{r})]](eqs/4356449759178279700-130.png) really means, and why it's such a useful object to consider. We'll start with
really means, and why it's such a useful object to consider. We'll start with  , then generalize to
, then generalize to 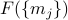 , and then finally talk about
, and then finally talk about ![F[phi(vec{r})]](eqs/4356449759178279700-130.png) .
.
To start off, we will introduce a fictitious ‘‘probe field’’  as a cute trick to easily calculate the magnetization
as a cute trick to easily calculate the magnetization  . After a Legendre transform, we will end up with the free energy
. After a Legendre transform, we will end up with the free energy 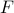 as a function of magnetization
as a function of magnetization  – and as we'll find,
– and as we'll find,  is a fantastic little object.
is a fantastic little object.
Note: In class we jumped directly into a spatially-varying magnetization density
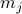 rather than beginning with a uniform
rather than beginning with a uniform  . I'm taking a different approach here.
. I'm taking a different approach here.
If time permits, we'll take a little detour to understand free energy, and why we care so much about it. Spoiler alert: the minima of the free energy tell you where equilibrium lies.
Armed with intuition about free energy, we'll explore the behavior of  (Landau theory), which will teach us many fabulous things:
(Landau theory), which will teach us many fabulous things:
a beautiful intuition for the behavior of second-order phase transitions
how you can find the magnetization density
 at any temperature by looking at the minima of
at any temperature by looking at the minima of 
a direct picture for how
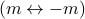 symmetry is broken when
symmetry is broken when 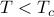
insight into how you can deduce the shape of
 merely with symmetry arguments
merely with symmetry argumentsand far more….
Once we've solidified our understanding of  , we'll move on and generalize
, we'll move on and generalize  to a spatially-varying magnetization density
to a spatially-varying magnetization density 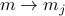 , which lets us account for textures in
, which lets us account for textures in 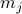 at different sites
at different sites  . Also, we'll discuss how to generalize from
. Also, we'll discuss how to generalize from  to an order parameter
to an order parameter 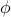 to describe all sorts of phase transitions beyond ferromagnetic ordering.
to describe all sorts of phase transitions beyond ferromagnetic ordering.
Then we'll take the continuum limit 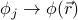 and pretend that the order parameter is defined everywhere in space
and pretend that the order parameter is defined everywhere in space 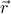 rather than just sites
rather than just sites  . This approach allows us to construct an order parameter field
. This approach allows us to construct an order parameter field 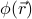 and to think about the free energy as a function(al) of the ‘‘texture’’ of the field (Landau-Ginzburg theory). If time permits, we'll also explain how to arrive at
and to think about the free energy as a function(al) of the ‘‘texture’’ of the field (Landau-Ginzburg theory). If time permits, we'll also explain how to arrive at 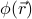 by coarse-graining. (Depending on how we cover the renormalization group later, this may or may not be useful!)
by coarse-graining. (Depending on how we cover the renormalization group later, this may or may not be useful!)
Finally, we'll discuss how we could have arrived at the shape of ![F[phi(vec{r})]](eqs/4356449759178279700-130.png) just by symmetry arguments. This sort of top-down or phenomenological approach is the sort of stuff that theorists fantasize about. The argument is simple, general, and powerful.
just by symmetry arguments. This sort of top-down or phenomenological approach is the sort of stuff that theorists fantasize about. The argument is simple, general, and powerful.
Motivation: Lingering Questions about Mean Field Approaches
We spent the last few weeks learning about the variational principle and mean field theory, but these appraoches still leave us with a few lingering questions.
Even though the variational principle tells us how to pick the ‘‘best’’ trial Hamiltonian, how do we know whether ‘‘best’’ is ‘‘good enough’’?
More precisely, even if we've minimized the variational free energy
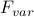 is minimized, how do we know whether we can trust its derivatives to tell us anything about correlation functions?
is minimized, how do we know whether we can trust its derivatives to tell us anything about correlation functions?
In our guess for the trial Hamiltonian, we assumed that every single site
 felt the same ‘‘mean field’’
felt the same ‘‘mean field’’ 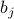 ; that is, we assumed a spatially uniform solution where
; that is, we assumed a spatially uniform solution where 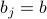 at all sites.
at all sites.How do we know whether a spatially uniform solution is actually the best possible solution?
More generally, can we come up with a simple and robust way to take into account the textures and spatial inhomogeneities of the mean field?
We spent so much time on the details of the Ising model, but do the results about its second-order phase transitions generalize to other systems?
Is there a conceptual framework that explains why the Ising model phase transition behaves as it does?
Can we argue how phase transitions ought to behave from a more general point of view?
As we'll see, the more sophisticated methods that we'll learn in class over the next few weeks will let us address some of these nagging questions which keep us up at night and gnaw at our sanity.
Outline
Bonus sections are marked with an *asterisk.
Movitivation
Can we trust the derivatives of the variational free energy?
How can we account for spatial variation and textures in the mean field of a material?
Can we generalize the features of phase transitions we found in the Ising model?
Probe fields are a nice trick to find magnetization. (Note: this page is a bit disorganized!)
*A trip down memory lane with Monsieur Legendre
Going from
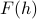 to
to 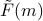 via Legendre Transform
via Legendre Transform
*Interlude: What exactly is free energy
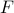 ?
?*Coming to terms with chemistry's curvy caricatures
*Minimizing free energy for fun and profit
*Landau theory – free energy as a function of magnetization

Deriving the Mean-Field Ising Free Energy
Spontaneous Symmetry Breaking!!! the phase diagram of second-order transitions <– Important!
How do things vary near
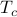 ? A taste of critical exponents <– Important!
? A taste of critical exponents <– Important!*Metastability, hysteresis, spinodals, nucleation, and all that jazz
Order Parameter Fields
Taking into account textures of magnetization:
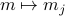
Other examples of order parameters and universality
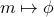
The continuum limit: the order parameter field
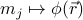
Example: phonons and fluids as classical fields
Theorist's Playground
Guessing Mr. Ginzburg's free energy
![F[phi(vec{r})]](eqs/4356449759178279700-130.png) from a top-down argument
from a top-down argumentSymmetry, universality, and deep implications
Internal order parameter symmetry vs spatial symmetry
Textures
Exponential decay from applied field at edges
Domain walls
General discussion: correlation length is only lengthscale!
Twisting order paramters with continuously broken symmetries
Anyways, enough babbling. Let's get started.