Table of Contents
Below I've included some commentary about my notes. The first half of my notes are very thorough, but the latter half gets more wishy-washy.
I've bolded my favorite pages.
First Lecture
In the beginning, I was just practicing how to write with a compelling voice. At this point, I didn't plan on publically sharing my notes yet.
Overview — an outline.
Phase Transitions — I'm quite happy with this page!
Symmetry — includes some derpy mspaint figures.
Ising Thermo — INCOMPLETE. A qualitative description of the Ising Model's phase diagram, including the Peierls free-energy argument for phase transitions in
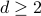 .
.
1D Ising Model
At the beginning of the course, we didn't have many good active learning worksheets, and we didn't have any solid resources with consistent notation. So I started writing these notes as a de facto resource.
Motivation — why we care about the 1D Ising model.
The Big Picture — the general framework of how to ‘‘solve’’ a model.
missing an intuitive explanation for thermodynamic concepts.
Exact Solution — works through the details of the transfer-matrix approach.
missing a section on diagonalizing the transfer matrix.
Mean Field Theory
This section is very thorough! I'm very happy with how it turned out.
Overview — Good motivation and summary.
Variational Principle — missing a proof of variational principle, which is irrelevant to the class anyways.
Non-interacting Spins — these next few pages are my favorite sections of the notes. The writing is vivid and clear-headed.
Mean-Field Ising Sol'n — a fun page to read.
Summary + Interp'n — a great way to review what happened.
Ginzburg-Landau Theory
By this point in the course, I got a bit burnt out from writing notes. A lot of the pages are incomplete, but I managed to write a good introduction for most of them.
Probe Fields — I discuss some interesting ideas here, but the page is rambly and incoherent.
What is Free Energy? — INCOMPLETE. I planned to discuss free energy from an intuitive standpoint.
Landau Theory — a very thorough page where I introduce the Landau Free Energy and calculate a few critical exponents.
Order Param Fields — INCOMPLETE. This page generalizes the Landau Free Energy into a continuously varying field.
Symmetry Arguments — INCOMPLETE. A shame, since the true power of Ginzburg-Landau theory is the way that we derive it from symmetry arguments.
Spatial Textures — INCOMPLETE. This page discusses situations where spatially varying solutions minimize the free energy.
Gaussian Model — Mostly complete. I'm just missing a more detailed discussion of how to calculate the correlation functions.
Applets! — Javascript applets!
Transport
For the last two weeks of the course, I had no reason to keep typing up my notes because we started using an actual textbook. So these pages are mostly incomplete.
Kinetic Theory — Mostly complete, just missing a few (unimportant) details on collision times and mean free paths.
Diffusion and Viscosity — INCOMPLETE.
Boltzmann Equation — INCOMPLETE.