![]()
From a quantitative point of view, there are two things we are interested about :
| lena.tif | Burt(0.4) | haar | Spline(1) | Burt(0.6) | Ideal | Spline(3) | Optimal linear(15) | Optimal cubic(15) | Approx Optimal NL | Median filter(3) | Previous sample as a predictor | minimum entropy predictor | |
| Entropy (bits/pel) | 7.44 | 6.19 | 5.94 | 5.73 | 5.69 | 5.67 | 5.61 | 5.55 | 5.43 | 5.39 | 5.35 | 5.03 | 4.61 |
The entropies of the linear methods are all higher than the ones obtained with other standard lossless techniques (simple causal linear predictive schemes). So with our assumptions, the pyramidal algorithm is not a good compression algorithm, unless we are interested in the progressive transmission feature.
|
|
Rate(bits/pel) |
|
Rate(bits/pel) |
|
Rate(bits/pel) | Avg Cost of reconstruction (Mflops) | |
| Approx optimal NL | 35.70 | 1.55 | 30.07 | 0.43 | 25.88 | 0.11 | 18 |
| Optimal cubic(15) | 35.39 | 1.57 | 29.66 | 0.44 | 25.63 | 0.12 | 3.2 |
| Optimal linear(15) | 34.60 | 1.62 | 29.32 | 0.46 | 25.42 | 0.12 | 1.6 |
| Ideal | 34.41 | 1.60 | 28.76 | 0.44 | 25.09 | 0.11 | 66.8 |
| Median filter(3) | 33.15 | 1.43 | 27.99 | 0.40 | 24.27 | 0.11 | 1.14 |
| Spline(3) | 31.59 | 1.63 | 24.54 | 0.46 | 19.28 | 0.12 | 35.4 |
| Spline(1) | 30.78 | 1.69 | 24.50 | 0.47 | 19.62 | 0.12 | 4.9 |
| Burt(0.6) | 30.35 | 1.57 | 24.12 | 0.44 | 19.24 | 0.11 | 7.8 |
| Burt(0.4) | 28.75 | 1.62 | 23.07 | 0.45 | 18.69 | 0.11 | 7.8 |
| haar | 28.30 | 1.63 | 22.71 | 0.44 | 19.23 | 0.12 | 0.11 |
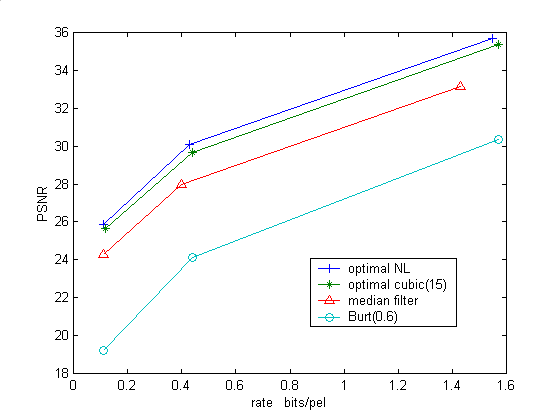
Figure : PSNR/Rate plot for the three levels of reconstruction of
lena
As we remove error images in the process of reconstruction of the image, we get rate-PSNR pairs as shown in the table and in the curve above. The overall shape of the curve is similar with slopes around 12 dB/bit for low bit rates and 5 dB/bits for high bit rates. Modifying the Expand-Reduce kernels yielded a 5dB improvement over the algorithm first introduced by Burt and Adelson.
This rate-PSNR curve does not compare well to those of optimal bit allocation pyramid coders as shown in class. There are several reasons for this. First, our scheme was first intented to be a lossless coder. Removing the lowest error levels in the pyramid is a very sub-optimal bit allocation scheme. Furthermore, the different rate-PSNR pairs were obtained in a single compression process while the examples stated in class optimize the distortion separately for each rate.
The advantage of this method is that no further computation is
necessary if the bit-rate is to be adaptated as required for network
transmission for instance.
![]()
