Pyramid coder with nonlinear prediction

Laurent MEUNIER
Antoine MANENS
EE368b (Image and Video compression)
Fall 2000

Introduction
The idea of a pyramidal image decomposition was first introduced by Burt
& Adelson [1] as a Compact Image Code. They envisioned it as a powerful
lossless technique to remove pixel-to-pixel correlation as well as a useful
tool for progressive transmission.
A pyramidal image is composed of one low resolution image along with all the higher resolution error images. For this
reason, the initial images can be recovered losslessly, which is a fundamental
condition of many fields (medical imagery and astrophysics are two examples
of such applications). The data reduction is obtained through a filtering
process that minimizes the variance of the error images.
In a progressive transmission scheme, an image is first sent at reduced
resolution (top of the pyramid) and the details are sent afterwards, bringing
with them some finer details to be superimposed to the interpolated low
resolution picture. In a similar way, we could imagine a protocol which
adapts the resolution to the rate of the connection : a PC user behind a
DSL
connection does not necessarily have the same exigencies as a Palm user.
In this context, a pyramid coder is the ideal tool.
Contrary to most traditional techniques such as transform techniques,
statistical modeling or linear filtering, pyramid coding offers a lot of
freedom as far as its operators are concerned. Linear operators
have been studied extensively. However, there is no reason to limit
ourselves to those
and some gains can be obtained by looking at non-linear operators.
We started by reviewing the existing linear and non-linear techniques.
The original paper by Burt & Adelson gave birth to the development
of all kinds of linear kernels and no work has been done on synthetizing
the performance of reconstruction of the existing filters in terms of PSNR
and of visual quality.
The observed limitation of the linear kernels motivated our non-linear approach that
gave us some improvement in
the context of lossless coding.
Slides of the presentation (Powerpoint
format)
Framework
Algorithm
The pyramidal algorithm has two operators :
-
REDUCE : a pre sampling filter followed by a down sampling by a factor
2
-
EXPAND : an up sampling by a factor 2 followed by an interpolation filter
The REDUCE operator produces a low passed version of the input signal and
using the result of the EXPAND algorithm, an error signal is produced.
The output signal is made of all the error images as well as of the
last low pass version : it contains all the information necessary to reconstruct
the original image (modulo the quantization errors).
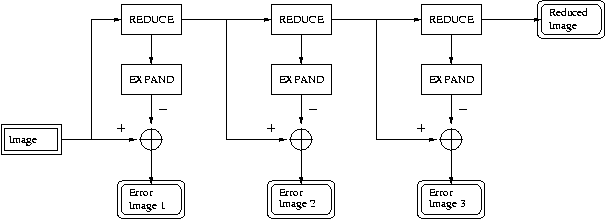
Figure : Open-loop pyramid coder. The information sent consists
of the error images and of the reduced image
From a compression point of view, the role of the pyramidal decomposition
is to concentrate the energy of the image in the sub sampled low pass version.
If we achieve this, the error images will have a low variance and we will
therefore be able to code them efficiently.
From a perceptual point of view, we want to reduce the aliasing
of the higher frequencies so that an image reconstructed to full size from
the lower definition error image gives a satisfying result.

Figure : Images transmitted in the pyramidal algorithm
We see that we don't have any restriction on the operator REDUCE and
EXPAND (unlike in wavelet decomposition or in sub band coding). They can
be non-linear in the general case.
The receiver gets the reduced image and the error images. The reduced
image is expanded using the same EXPAND as the coder and the error images
are
added at each step of the pyramid to add the details to the image.
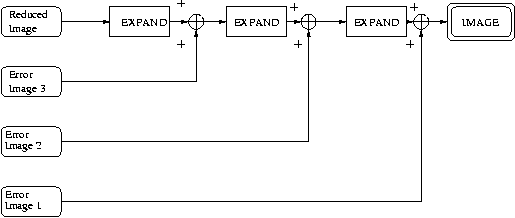
Figure : Expansion of the image.
One of the feature we focused on in this study is the progressive transmission.
If the cost of the transmission of the reduced image can be low, the cost
of the transmission of the error images increases by a factor of 4 each
time. However, as shown in the next figure, all levels are not necessary
to obtain a recognizable picture.

Figure : Different steps of the reconstruction of the image (left
to right, top to bottom)
Quantization
Entropy can be substantially reduced by quantizing the pixel values in
each level of the Laplacian pyramid [1]. When a proper choice of the number
and of the distribution of the quantization levels is made, the degradation
due to quantization is almost imperceptible (e.g. the human eye is fairly
sensitive to contrast perturbations at low and medium spatial frequencies
but relatively less to such perturbations at high spatial frequencies).
However, we did not concentrate on this aspect. We concentrated on lossless coding and the quantization simply consisted
of rounding to the nearest integer value. This way, the distinction between
open and closed pyramidal coding is not relevant any more since the reconstruction
is nearly perfect at each step. Most importantly, the inherent quality of
the REDUCE-EXPAND scheme can be assessed without any side-effects coming
from other aspects of the coding pipeline.
Coding
We made a few assumptions as far as how the coding was done. All the levels
of the pyramid are coded separately using a different Variable Length Code
: it permitted a significant improvement over a coding with the same VLC for the pyramid.
If the error images have more or less the same histogram of values, the
reduced resolution has completely different statistical properties.
The final rate was obtained by adding the weighted entropy of the
images
(i.e. assuming an ideal VLC coder) rather
than actually coding the images by Huffman coding. Moreover, we did not
include the cost of sending the coding table, which can be non-negligible
as we increase the number of levels of the pyramid : it would be probably
more realistic to code the smaller error images with the same VLC. An
other approach could consist of using a pre computed VLC coder using the
statistics of the pyramid levels.
Implementation
Matlab was used for all the programming. The performances were quite good
because the pyramidal algorithms is usually well expressed in terms of matrix
operations.
Criteria
We based our comparison of the filters on several criteria :
-
compression rate : what is the efficiency of the transmission scheme ?
-
visual aspect : how well are the edges are preserved at lower resolution, what
is the intensity of the blurring, etc... ?
-
aliasing : this point is highly related to the previous one. The only source
of aliasing is the pre-sampling filter used in REDUCE.
-
flops : we don't want the method to be too computationaly expensive.
 Next (Linear techniques)
Next (Linear techniques)





![]()
