Due July 8th, 11:59pm.
Written by Chris Piech and Percy Liang.
Instructions
This problem set has three problems that you should submit an answer for (Scripto Coninua, Searchable Maps and Autonomous TA). Write your solutions to each of the three problems in separate documents and save them to files named p1.pdf, p2.pdf and p3.pdf.
The assignment is to be submitted as follows.
Log onto a corn machine, put your solution pdf into a directory on the Stanford AFS space. Go into the directory that contains your source code. Then type:
/usr/class/cs221/submitter/submit
You can submit multiple times and we will grade your latest submission -- so feel free to submit a lot.
In fact why don't you try submitting right now (yes now). If you have problems submitting, please contact the TAs immediately. See submitting for more details.
0. Welcome Email
Look up your TA:
and send an introductory e-mail to your TA and to Chris Piech (piech@cs.stanford.edu).
Here's the information to include in your e-mail:
| a | Your name |
| b | Why you decided to take CS221. |
| c | What you are most looking forward to about the class. |
| d | What you are least looking forward to about the class. |
| e | Any suggestions that you think might help you learn and master the course material. |
And if you feel like giving us a little more to remember you by, you could also tell us what do you do for fun and/or tell us a quick anecdote about something that makes you unique -- a talent, an unusual experience, or anything of that sort.
1. Scripto Continua
In some languages such as Chinese, and in some English web domains, sentences are written without spaces between the words. An important first step in language processing is segmenting sequences of characters into words.
Figure 1: A sentence in Mandarin and two possible segmentations.
D
, which is the set of all words in a language (each word is also a sequence of characters). The goal of sentence segmentation is to split the sentence into words from the dictionary. For example in english, if
D = {i,cat,dog,see,sleep,the}
, then given the characters
iseethecat
,
[i, see, the, cat]
is a possible segmentation.
| a | Suppose maximizing our utility corresponds to minimizing the number of words in the output segmentation. Construct a deterministic state space model for this task. |
| b | What search algorithms (out of the following, BFS, DFS, UCS, A*, Bellman-Ford) would produce a minimum cost path for your model and why? |
| c | If our goal is to maximize the number of words in the segmentation, revise the state space model from above. Which search algorithms work now? |
| d |
Instead of minimizing the number of words in the segmentation, suppose we had at our disposal a function $\text{Fluency}(w_1, w_2)$ which returns a number (either positive or negative) representing the compatibility of $w_1$ and $w_2$ being next to each other (for example, $\text{Fluency}(an, cat)$ would be low and $\text{Fluency}(a, cat)$ would be high). Suppose our utility function is the sum of the fluencies of adjacent words; formally, if the segmentation produces words $w_1, \dots, w_n$, then the utility is $\sum_{i=2}^n \text{Fluency}(w_{i-1}, w_i)$. Modify the state space model from above to find the most fluent segmentation. |
2. Searchable Maps
In the US road network there are over 24 million nodes and over 58 million edges. Even on a state of the art computer with an optimized implementation of bi-directional dijkstra, calculating the fastest route between a random start node $s$ and a random end node $t$ can take a few seconds. Google Maps (for example) performs these queries in a fraction of that time. In this problem we will unravel how we can use A* search towards handling a real sized road network.
Figure 2: The fastest path for Santiago the protagonist of the Alchemist. Santiago had to follow his dreams. Google used an advanced search algorithm and plotted a more efficient journey in a fraction of a second.
| a | The Haversine distance between points $a$ and $b$ written $G(a, b)$ is the distance between two points along the surface of the earth. Let $S_H$ and $S_L$ be the maximum speed and the minimum speed that a car is allowed to travel on any road respectively. Define a consistent heuristic for a search for the fastest path from $s$ to $t$ based on their Haversine distance. |
| b | It is infeasable to precompute and save the fastest path between every two nodes (there are over 500 trillion pairs in the US network alone), but it is possible to compute and store the fastest path between every node and a single landmark. Let $T(a, L)$ be the amount of time it takes to get from node $a$ to landmark $L$.
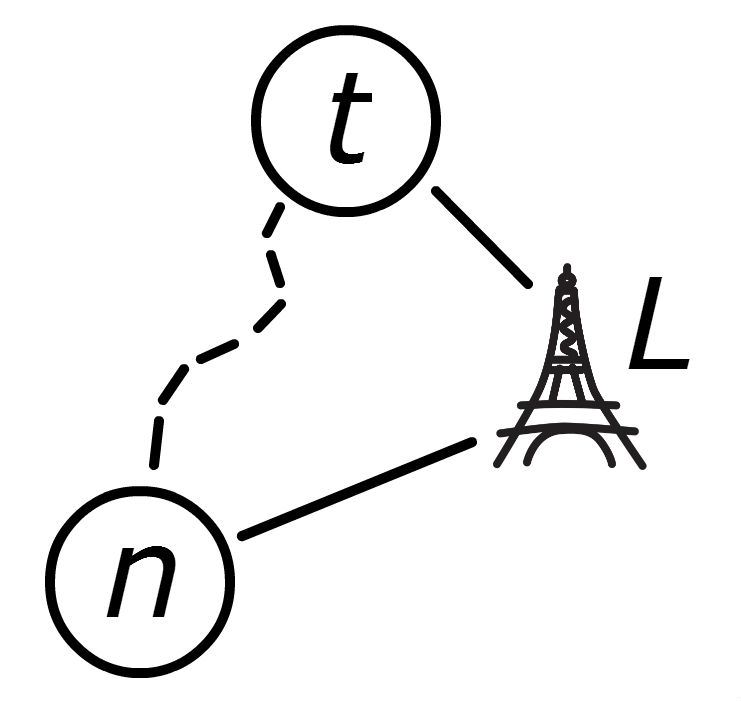
Figure 3: The triangle of distances between points $n$, $t$ and a landmark $L$. |
| c | Let $h_1$ and $h_2$ be consistent heuristics. Define a new heuristic $h(s) = \max\{h_1(s), h_2(s)\}$. Prove that $h$ is consistent. |
| d | Let's say you have $K$ landmarks $(L_1, L_2, ... , L_K)$. Use the intuition from part (c), and your heuristics from parts (a) and (b) to create a single fastest path heuristic function. |
| e | Sometimes new roads are constructed, and sometimes roads are closed for repair. Suppose a heuristic $h$ is consistent for a particular state space model. If new edges are added to the search space graph, does $h$ remain consistent for the new model? What if edges are removed? In both cases, give a proof or a counterexample. |
| f | Optional: Think up your own improvement over the base Dijkstra algorithm for finding the fastest path between two points. Alternatively how would you solve this problem if you were optimizing something other than speed (e.g. how beautiful a route is)? |
3. Autonomous TA
Due to the use of computer tools in education, there is a unprecedented amount of data on how students learn which has enabled new artificial intelligence research topics. In this problem our objective is to write an autonomous TA who can give hints (at the optimal time) to a student who is working on a homework assignment $H$.
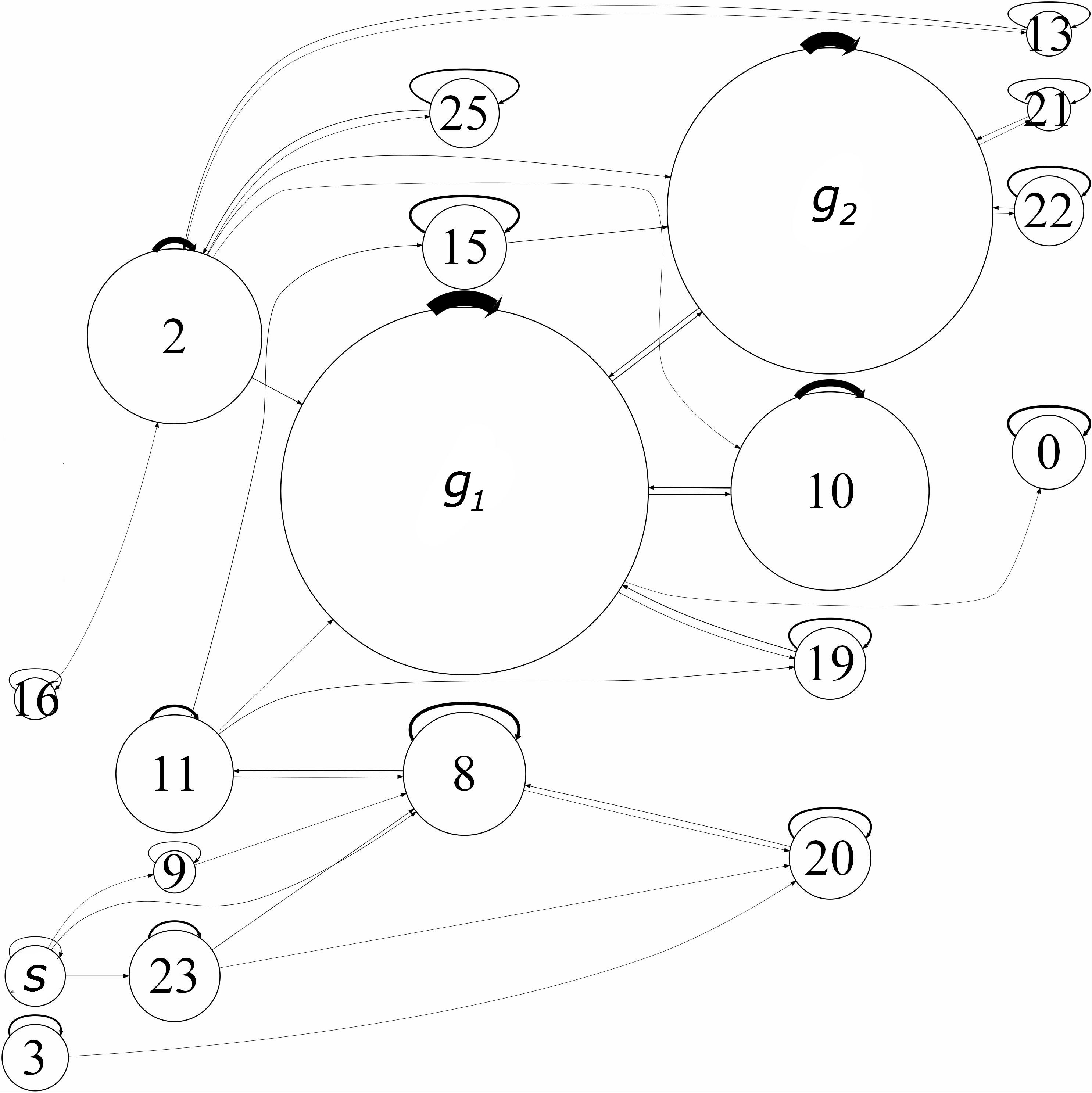
Figure 4: The state machine for CS106A students solving Checkerboard Karel. The state machine depicts the probability of a student being in a node and the probability of a student changing states. Node $s$ is the starter code and $g_1$ and $g_2$ are two solutions. Hints received by students (and how they affect the state transitions) are not displayed.
Hints:
For homework $H$ both the human TAs and our new autonomous TA are only allowed to give hints from a predetermined set of 5 hints. We will assume each hint can (and should) only be given to a student once.
Dataset:
In the past tens of thousands of students have solved $H$ using our editor. For each of the past students we have:
- A copy of the students partial solutions, saved in 5 minute intervals as they solve $H$.
- A history of the hints that the student has received from a human TA in-between each five minute interval.
- The student's midterm score.
Not all students complete the assignment. There are a few states which are correct solutions, but a student can stop at any time.
Discretization:
To make our problem discrete we have chosen a set of 30 most representative
states
that a student's partial solution can be in and we have created a function
nearest(studentsWork)
that returns the best fit
state
for any solution or partial solution. A state could be something like "the student hasn't started yet" or "the student has solved the first subproblem using algorithm $x$."
Task:
Formalize the task of chosing which (if any) hint our autonomous TA should give to a new student at a particular time as a Markov Decision Problem where the TA also considers what future hints it will give. The objective we want to maximize will be the student's expected midterm grade. For this problem we are going to make the assumption that a student's next state is a probabilistic event that depends on the student's current state and the autonomous TA's action but that it is unaffected by the student's previous states and TA's previous actions. For each part of your formalization explain briefly how you could compute the necessary values using the past students data.
There are many different solutions to this problem. The expectation is that your formalization would reasonably allow a TA to give an autonomous hint. Creative solutions will be considered as extra credit.