Deterministic Search Problems (DSPs) are useful. However very few situations in life have actions with deterministic successor states. Markov Decision Problems (MDPs) extend DSPs by modeling the generation of successor states (given a known previous state and a given action) as a probability distribution called a Transition Probability. By relaxing our model we are able to solve a much richer set of problems.

One way to think of the difference between DSPs and MDPs: DSPs are state search problems where the agent is playing against herself. MDPs are state search problems where the agent is playing against nature. As such for each round aka ply, the agent gets to chose an action and then nature, ambivilantly, choses a successor state.

As an important note, though our successor states are now going to be generated using a probability distribution, this does not mean that there is necessarily some part of the world that is metaphorically "rolling dice." Instead, in many Markov Decision Problems, using a probabilistic distribution to represent the generation of successor states reflects that we, as agents, may be uncertain about a potentially certain world.

Turning a real world problem into a Markov Decision Problem is almost identical to turning a real world problem into a Deterministic Search Problem. The main difference is that for a MDP instead of specifying the successor of a (state, action) pair, you specify a probability distribution over successor states.

It is important to be precise about the assumptions that still exist in MDPs, in addition to the Markov assuption. Markov Decision Problems assume that (a) the world exists in discrete states, (b) the start state is known and (c) we know the legal moves from any state. These do not always fit perfectly to the real world, but allow for a computer to create and search the corresponding decision tree.

One useful limitation to place on our models is to make sure that they have a "finite horizon." Put simply, it is useful if the state search tree (the one that your formulation describes) is not infinetly deep. If you describe a Markov Decision problem with an infinite horizon, you will need a more specialized solver.

Here is an example MDP expressed as a tree. In this example the agent (Snowden) is in a deterministic state, and can take actions from a discrete set (eg fly to Moscow). However the resulting states (eg be in Moscow) after he takes an action occur with given probabilities:

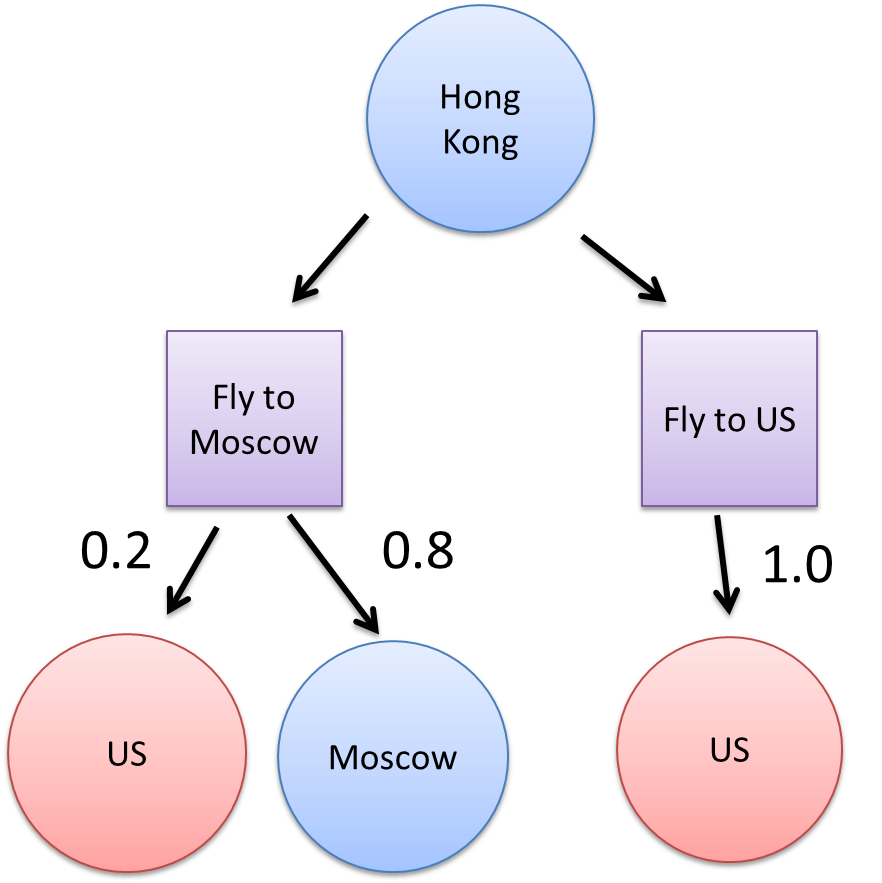
Inference is the orthodox term for the act of applying an algorithm to a formalized problem in order to come up with an answer. There are generally two goals of inference on Markov Decision Problems: (1) Having an agent chose an action given a current state, (2) creating a policy of how agents should act in every possible state. In CS221 are only going to focus on the former (but please come see the staff if you are interested in learning more about policy inference).

Expectimax is an inference algorithm for Markov Decision Problems that allows an agent to select a "utility" maximizing action for a given state. The algorithm is a variant of exhaustive depth-first search which takes advantage of the recursive definition of utility. For every state and for every action in the search tree the algorithm assigns a utility. The utility of a state is the maximum utility of any of the legal actions from that state:
And the utility of an action is its expected utility: For all possible resulting states, the probability of that resulting state is multiplied by its utility.

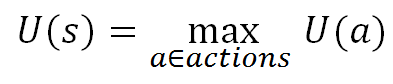
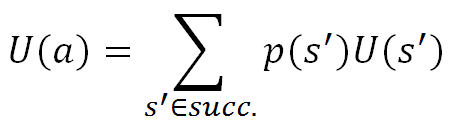
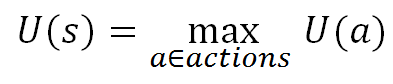
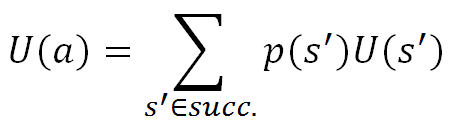
Expectimax gets its name because the rows of the search tree alternate from being utility is the expectation of the children to utilities are the max of the children.

Sometimes, for real world problems the transition distrubutions are known. For example in the pac-man problem, RandomGhost choses a successor state uniformly.

In the situations where the transition distributions are not obvious (read: almost every real world example) you must formulate a way to calculate your transition probabilities. Generally these probabilities are learned by watching the world. The easiest way to learn a probability distribution by observation is to "count." Given enough training examples, you can count the fraction of times a given state action pair, s, a resulted in successor state s' and report that fraction as your transition probability. Later on in the class we will cover more advanced ways of learning probability distributions for Markov Decision Problems.