Gibbs Sampler Examples¶

Bivariate Normal¶

Suppose we want to simulate from a centered bivariate normal (\(\mu=0\)) with correlation \(\rho\) and variances both 1 and we know that \(X|y \sim \mathcal{N}(\rho y,1-\rho^2)\) (A proof can be found here ):

##########################################Function######
gibbsNimate <- function(NSimul=50, rho=0.5, x0=1, y0=1)
{
  ##NSimul=Number of simulations
  ##rho is the correlation
  ##x0 and y0 are the starting values
  ## plot the 95% contour of the theoretical normal
  ##
  plot(ellipse(rho), type="l",
   main="Bivariate Normal", col="green")
      dev.hold()
  ## initialization
  x <- rep(0, NSimul)
  y <- rep(0, NSimul)
  x[1]=x0
  y[1]=y0
  ## Gibbs sampler and plot points

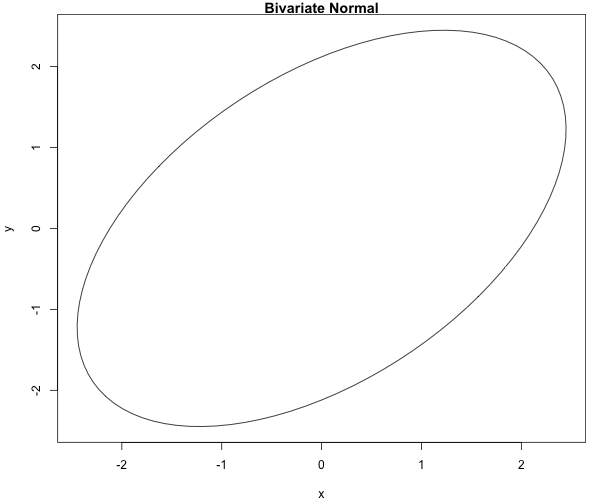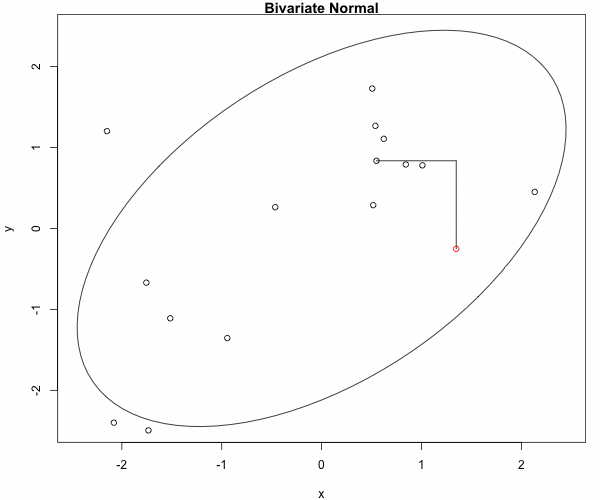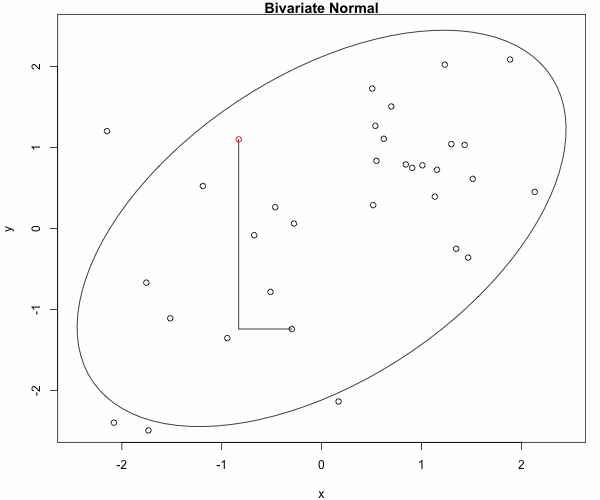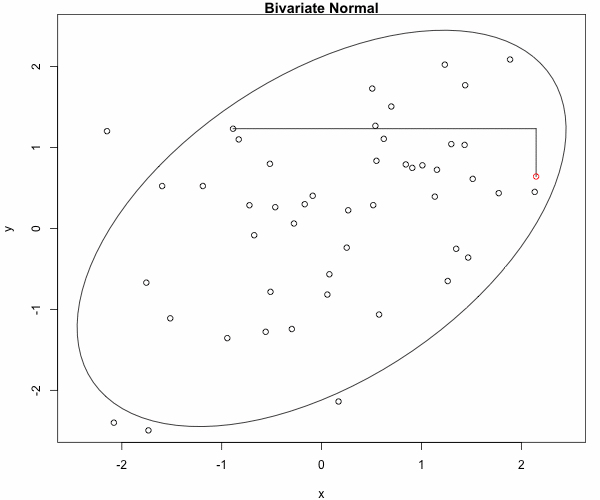
  for(b in 2:NSimul) {
     plot(ellipse(rho), type="l",
               main="Bivariate Normal")
  points(x[1:(b-1)], y[1:(b-1)])
  dev.hold()
    ## sample the x direction conditional on y
  x[b] <- rnorm(1, rho*y[b-1], sqrt(1-rho^2))
  lines(c(x[b-1], x[b]), c(y[b-1], y[b-1]))
  ## sample the y direction conditional on x
  y[b] <- rnorm(1, rho*x[b], sqrt(1-rho^2))
  lines(c(x[b], x[b]), c(y[b-1], y[b]))
  ani.pause()
  points(x[b], y[b],col="red")
  }
  ## return the draws
  return(cbind(x,y))
}

If we run this function with a correlation of 0.5.

#################
require(ellipse)
require(animation)
#oopt = ani.options(interval = 2)
#gibbsNimate(50,rho=0.5)

We obtain the 50 first steps:

animatedgif