PCA, SVD and MDS

SVD notation and example

\[\begin{split}{\bf X}_{n\times p}= U_{n\times p}S_{p\times p}V_{p\times p}', V'V=I_p, U'U=I_p. {\bf S}_{p\times p}= \left(\begin{array}{lccr} s_1 &0& \cdots& 0\\ 0 & s_2 & \cdots& 0\\ 0 & \cdots & s_{k-1}& 0\\ 0 & 0 & \cdots& s_{k}\\ \end{array} \right)\end{split}\]

where r is the rank of X.

Generating a rank three matrix

Now we have generated an approximately rank three matrix.

>  load("/Users/susan/sphinx/data/SVD3ex.save")
>  svd(X3)$d
[1] 7.000000e+00 5.000000e+00 3.000000e+00 5.010064e-16 4.021512e-16
[6] 1.811002e-16
>  res3=eigen(t(X3)%*%X3)
>  svd(X3)$d^2
[1] 4.900000e+01 2.500000e+01 9.000000e+00 2.510074e-31 1.617256e-31
[6] 3.279727e-32
>  require(ade4)
>  X3.pca=dudi.pca(X3,scannf=F,nf=4)
>  X3.pca$eig
[1] 3.7555053 2.2097216 0.0347731
>  X3.pca$co
        Comp1       Comp2      Comp3
V1 -0.7575077  0.63614665 0.14662713
V2 -0.8207017 -0.57009027 0.03802406
V3 -0.4067514 -0.91303611 0.03030472
V4  0.6277681 -0.77564837 0.06539690
V5  0.9958962 -0.06702507 0.06081494
V6  0.9781551  0.20069475 0.05416792
> 

So, the output from the SVD, Eigendecomposition and PCA are not the same?

Why Not?

Well, for PCA the default is for the matrix to be centered by columns first, so if we don’t do that, we should get the same as above, let’s try it.

> load("/Users/susan/sphinx/data/SVD3ex.save")
> require(ade4)
> X3.pca=dudi.pca(X3,scannf=F,nf=4,center=F)
> X3.pca$co
        Comp1      Comp2       Comp3
V1 -0.3660850  0.7285115  0.57901015
V2 -0.7381575  0.5827776 -0.33984369
V3 -0.9403123  0.1881923 -0.28354248
V4 -0.9870967 -0.1504679 -0.05476738
V5 -0.9225645 -0.3586531  0.14227646
V6 -0.8400384 -0.4695396  0.27178662
> res3$vectors[,1]
[1] -0.7364928 -0.4432826 -0.3274789 -0.2626469 -0.2204199 -0.1904420
> 

Not right yet, so not only does the dudi.pca center the data but by default it also rescales it so that all the variables (columns) have variance 1, so let’s try not rescaling or centering.

> load("/Users/susan/sphinx/data/SVD3ex.save")
> require(ade4)
> X3.pca=dudi.pca(X3,scannf=F,nf=4,center=F,scale=F)
> X3.pca$co[,1]
[1] 1.7184832 1.0343260 0.7641174 0.6128427 0.5143130 0.4443648
> sum(X3.pca$co[,1]^2)
[1] 5.444444
> X3.pca$eig
[1] 5.444444 2.777778 1.000000
> 

and see that by coincidence the first eigenvalue matches the norm of the component in the co (columns) part of X3.pca. In fact if we look at the normalized component which is in X3.pca$c1, we have an exact match:

> load("/Users/susan/sphinx/data/SVD3ex.save")
> require(ade4)
> X3.pca=dudi.pca(X3,scannf=F,nf=4,center=F,scale=F)
> X3.pca$c1
         CS1        CS2        CS3
V1 0.7364928  0.6225002 -0.2550021
V2 0.4432826 -0.1818705  0.6866860
V3 0.3274789 -0.3508553  0.2611139
V4 0.2626469 -0.3921783 -0.1043599
V5 0.2204199 -0.3945644 -0.3509658
V6 0.1904420 -0.3831871 -0.5110654
> res3$vectors[,1]
[1] -0.7364928 -0.4432826 -0.3274789 -0.2626469 -0.2204199 -0.1904420
> 

Now we can make the eigendecomposition match in the other direction: Start with X3 then center and scale it and check that its svd and eigenvectors correspond to the simple PCA:

> load("/Users/susan/sphinx/data/SVD3ex.save")
> require(ade4)
> X3sc=scale(X3)
> apply(X3sc,2,mean)
[1] -2.464151e-17  5.551115e-17 -2.463548e-17  1.853534e-17 -1.048424e-16
[6]  7.250903e-17
> apply(X3sc,2,sd)
[1] 1 1 1 1 1 1
> eigen(t(X3sc)%*%X3sc)
$values
[1]  3.004404e+01  1.767777e+01  2.781848e-01  1.036812e-15  4.897449e-16
[6] -8.461922e-16

$vectors
           [,1]        [,2]      [,3]       [,4]        [,5]       [,6]
[1,] -0.3908885  0.42794551 0.7863079  0.0000000  0.00000000  0.2139829
[2,] -0.4234978 -0.38350838 0.2039092  0.2289084 -0.09038418 -0.7559257
[3,] -0.2098915 -0.61421324 0.1625132 -0.6840457  0.15154090  0.2477779
[4,]  0.3239404 -0.52179043 0.3506998  0.6044730  0.11955955  0.3465904
[5,]  0.5139015 -0.04508878 0.3261284 -0.2623778 -0.72797696 -0.1694697
[6,]  0.5047468  0.13501040 0.2904828 -0.2131961  0.65162958 -0.4153901

> res3c=dudi.pca(X3sc,nf=6,scannf=F)
> res3c$c1
          CS1         CS2       CS3
V1 -0.3908885  0.42794551 0.7863079
V2 -0.4234978 -0.38350838 0.2039092
V3 -0.2098915 -0.61421324 0.1625132
V4  0.3239404 -0.52179043 0.3506998
V5  0.5139015 -0.04508878 0.3261284
V6  0.5047468  0.13501040 0.2904828
> res3c$eig
[1] 3.7555053 2.2097216 0.0347731
> eigen(t(X3sc)%*%X3sc)$values[1]/res3c$eig[1]
[1] 8
> 

Summary of things we noticed

1. Usually PCA does an eigendecomposition of the crossproduct of the standardized, recentered matrix divided by (n-1), we call this matrix the correlation matrix.
2. The square of the singular values are the eigenvalues.
3. The principal components have their norm equal to the eigenvalue.
4. Each eigenvalue actually gives the variance explained by that component (ie. the first eigenvalue gives the variance explained by the first component)

R code for cut and paste

rm(X)
 load("/Users/susan/sphinx/data/SVD3ex.save")
 svd(X3)$d
 res3=eigen(t(X3)%*%X3)
 svd(X3)$d^2
 #Comparing   the ouput from a PCA and an SVD?
 require(ade4)
 X3.pca=dudi.pca(X3,scannf=F,nf=4)
 X3.pca$eig
 X3.pca$co
load("/Users/susan/sphinx/data/SVD3ex.save")
require(ade4)
X3.pca=dudi.pca(X3,scannf=F,nf=4,center=F)
X3.pca$co
res3$vectors[,1]
load("/Users/susan/sphinx/data/SVD3ex.save")
require(ade4)
X3.pca=dudi.pca(X3,scannf=F,nf=4,center=F,scale=F)
X3.pca$co[,1]
##still not right, but we can remark a funny thing,
##the sums of squares of this vector are equal to:
sum(X3.pca$co[,1]^2)
####we compare this to
X3.pca$eig
load("/Users/susan/sphinx/data/SVD3ex.save")
require(ade4)
X3.pca=dudi.pca(X3,scannf=F,nf=4,center=F,scale=F)
X3.pca$c1
res3$vectors[,1]
load("/Users/susan/sphinx/data/SVD3ex.save")
require(ade4)
X3sc=scale(X3)
apply(X3sc,2,mean)
apply(X3sc,2,sd)
eigen(t(X3sc)%*%X3sc)
res3c=dudi.pca(X3sc,nf=6,scannf=F)
res3c$c1
res3c$eig
##What's the relationship between the eigenvalues,
###there must be one (the evectors are the same)
eigen(t(X3sc)%*%X3sc)$values[1]/res3c$eig[1]

PCA and MDS(multidimensional scaling)

We want to compute a matrix of distances between rows of X:

> load("/Users/susan/sphinx/data/SVD3ex.save")
> X3c=sweep(X3,2,apply(X3,2,mean))
> B=crossprod(t(X3c))
> DX2=as.matrix(dist(X3c))^2
> DX2c=sweep(DX2,1,apply(DX2,1,mean))
> cDX2c=sweep(DX2c,2,apply(DX2c,2,mean))
> apply(cDX2c,1,mean)
            1             2             3             4             5 
 1.185202e-15 -3.455955e-16 -4.933361e-16  1.974031e-16 -6.413176e-16 
            6             7             8             9 
-6.910464e-16 -7.896365e-16 -2.961077e-16  0.000000e+00 
> apply(cDX2c,2,mean)
            1             2             3             4             5 
-1.579369e-15  0.000000e+00 -1.481020e-16  0.000000e+00 -1.972284e-16 
            6             7             8             9 
 0.000000e+00 -1.477888e-16 -4.943962e-17  2.470053e-16 
> B[1:4,1:4]
          [,1]     [,2]       [,3]       [,4]
[1,] 25.982036 2.700244 -2.2400063 -3.8056073
[2,]  2.700244 5.585367  2.6459863  0.4513750
[3,] -2.240006 2.645986  1.7776930  0.8125225
[4,] -3.805607 0.451375  0.8125225  0.7202679
> cDX2c[1:4,1:4]
           1          2         3         4
1 -51.964071  -5.400488  4.480013  7.611215
2  -5.400488 -11.170735 -5.291973 -0.902750
3   4.480013  -5.291973 -3.555386 -1.625045
4   7.611215  -0.902750 -1.625045 -1.440536
> resd=eigen(-cDX2c/2)
> resd$values[1:4]
[1] 3.168252e+01 9.959124e+00 1.039780e-01 3.019306e-15
> resd$vectors[,1]
[1]  0.89037645  0.16714282 -0.03608682 -0.11829470 -0.15691910 -0.17631939
[7] -0.18617646 -0.19092439 -0.19279842
> res.mds=cmdscale(dist(X3),k=4,eig=TRUE)
> res.mds$points[,1]
[1]  5.0116824  0.9408006 -0.2031227 -0.6658481 -0.8832541 -0.9924530 -1.0479357
[8] -1.0746605 -1.0852089
> res.mds$eig[1:4]
[1] 3.168252e+01 9.959124e+00 1.039780e-01 1.610435e-15
> require(ade4)
> res.pca=dudi.pca(X3,nf=4,scannf=F,scale=F)
> res.pca$li[,1]
[1] -5.0116824 -0.9408006  0.2031227  0.6658481  0.8832541  0.9924530  1.0479357
[8]  1.0746605  1.0852089
> res.mds$eig[1:3]/res.pca$eig[1:3]
[1] 9 9 9
> 

R code for cut and paste

load("/Users/susan/sphinx/data/SVD3ex.save")
X3c=sweep(X3,2,apply(X3,2,mean))
B=crossprod(t(X3c))
DX2=as.matrix(dist(X3c))^2
DX2c=sweep(DX2,1,apply(DX2,1,mean))
cDX2c=sweep(DX2c,2,apply(DX2c,2,mean))
apply(cDX2c,1,mean)
apply(cDX2c,2,mean)
B[1:4,1:4]
cDX2c[1:4,1:4]
resd=eigen(-cDX2c/2)
resd$values[1:4]
resd$vectors[,1]
####Now we compare with the output of what is known as classical MDS (multidimensional scaling).
res.mds=cmdscale(dist(X3),k=4,eig=TRUE)
res.mds$points[,1]
res.mds$eig[1:4]
require(ade4)
res.pca=dudi.pca(X3,nf=4,scannf=F,scale=F)
res.pca$li[,1]
######We can also compare the eigenvalues
res.mds$eig[1:3]/res.pca$eig[1:3]

Examples of Using MDS just on distances

> eck=read.table("/Users/susan/sphinx/data/eckman.txt",header=TRUE)
> eck[1:4,1:4]
  w434 w445 w465 w472
1 0.00 0.86 0.42 0.42
2 0.86 0.00 0.50 0.44
3 0.42 0.50 0.00 0.81
4 0.42 0.44 0.81 0.00
> require(ade4)
> queck=quasieuclid(as.dist(1-eck))
> eck.pco=dudi.pco(queck,scannf=F,nf=2)
> 

> eck=read.table("/Users/susan/sphinx/data/eckman.txt",header=TRUE)
> require(ade4)
> queck=quasieuclid(as.dist(1-eck))
> eck.pco=dudi.pco(queck,scannf=F,nf=2)
> biplot(eck.pco,posi="bottomright")
> 

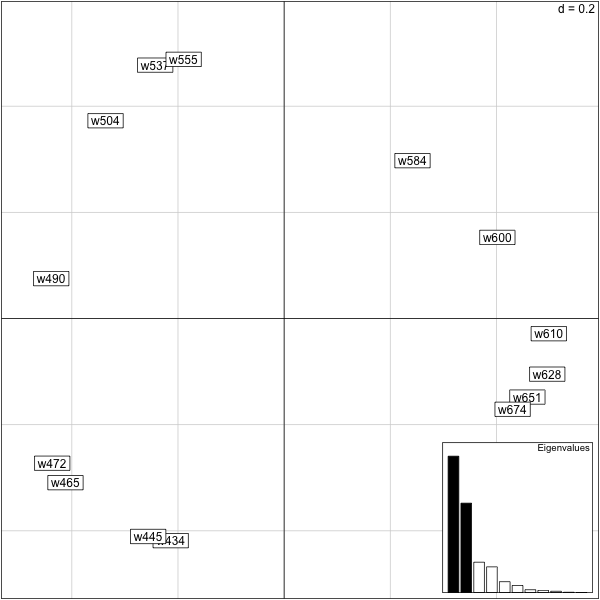
Typical ouput from PCoA and PCA type methods include horseshoes and arches if there is an underlying gradient. For a talk about this in the case of election data see slides horsehoe, Holmes and the paper.

R code for cut and paste

###Eckman's confusions of colors data
eck=read.table("/Users/susan/sphinx/data/eckman.txt",header=TRUE)
eck[1:4,1:4]
require(ade4)
queck=quasieuclid(as.dist(1-eck))
eck.pco=dudi.pco(queck,scannf=F,nf=2)
eck=read.table("/Users/susan/sphinx/data/eckman.txt",header=TRUE)
require(ade4)
queck=quasieuclid(as.dist(1-eck))
eck.pco=dudi.pco(queck,scannf=F,nf=2)
biplot(eck.pco,posi="bottomright")

Summary of facts about PCA and MDS

1. If we have the orginal n by p table of data (X), then a standard PCA and a classical MDS will give the same components. This is why MDS is also called PCoA or Principal Coordinate Analysis.
2. The eigenvalues are different - changed by a coefficient.
3. MDS can be used on data for which we do not know coordinates, only the relative distances.

References

Usually it takes a whole course to go through all the multivariate methods, here is such a course.

For a quick refresher on eigenvectors, there is a nice informative video about eigenvalues and eigenvectors at Khan academy EV.