Hidden Markov Models - the Unfair Casino¶
Preparation¶
Good reading material:¶
Article by Sean Eddy: (good review article on what a hidden Markov model is) http://www.nature.com/nbt/journal/v22/n10/full/nbt1004-1315.html
Animated website:
http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/main.html
Book chapter where the unfair casino was first presented:
Biological sequence analysis (probabilistic models of proteins and nucleic acids)
Durbin, Eddy Krogh and Mitchison, Cambridge university press
Model¶
- State Space (suppose we have two: fair dice /loaded dice)
- Switch between two states is according to a given matrix (Markov transition matrix)
- Output is probabilistic but depends on the state (fair/loaded)
- Want to guess the hidden state (fair/loaded) from the output observed (here tosses of the die).
Examples in R¶
> require(HMM)
Loading required package: HMM
> nSim = 2000
> States = c("Fair", "Unfair")
> Symbols = 1:6
> transProbs = matrix(c(0.99, 0.01, 0.02, 0.98), c(length(States),
+ length(States)), byrow = TRUE)
> emissionProbs = matrix(c(rep(1/6, 6), c(rep(0.1, 5), 0.5)),
+ c(length(States), length(Symbols)), byrow = TRUE)
> hmm = initHMM(States, Symbols, transProbs = transProbs, emissionProbs = em
issionProbs)
> sim = simHMM(hmm, nSim)
> vit = viterbi(hmm, sim$observation)
> f = forward(hmm, sim$observation)
> b = backward(hmm, sim$observation)
> i <- f[1, nSim]
> j <- f[2, nSim]
> probObservations = (i + log(1 + exp(j - i)))
> posterior = exp((f + b) - probObservations)
> x = list(hmm = hmm, sim = sim, vit = vit, posterior = posterior)
> mn = "Fair and unfair die"
> xlb = "Throw nr."
> ylb = ""
>
R code for cut and paste¶
rm(X)
#############you must install the package HMM
#### dishonestCasino()
require(HMM)
nSim = 2000
States = c("Fair", "Unfair")
Symbols = 1:6
transProbs = matrix(c(0.99, 0.01, 0.02, 0.98), c(length(States),
length(States)), byrow = TRUE)
emissionProbs = matrix(c(rep(1/6, 6), c(rep(0.1, 5), 0.5)),
c(length(States), length(Symbols)), byrow = TRUE)
hmm = initHMM(States, Symbols, transProbs = transProbs, emissionProbs = emissionProbs)
sim = simHMM(hmm, nSim)
vit = viterbi(hmm, sim$observation)
f = forward(hmm, sim$observation)
b = backward(hmm, sim$observation)
i <- f[1, nSim]
j <- f[2, nSim]
probObservations = (i + log(1 + exp(j - i)))
posterior = exp((f + b) - probObservations)
x = list(hmm = hmm, sim = sim, vit = vit, posterior = posterior)
##Plotting simulated throws at top
mn = "Fair and unfair die"
xlb = "Throw nr."
ylb = ""
���������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
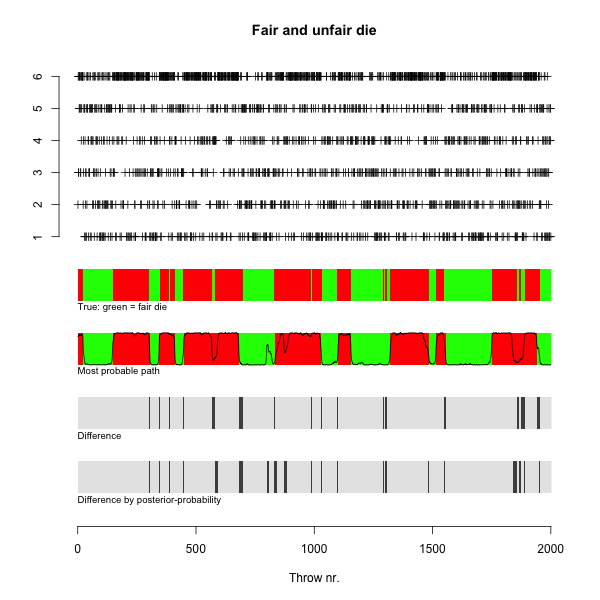
> plot(x$sim$observation, ylim = c(-7.5, 6), pch = 3, main = mn,
+ xlab = xlb, ylab = ylb, bty = "n", yaxt = "n")
> axis(2, at = 1:6)
> text(0, -1.2, adj = 0, cex = 0.8, col = "black", "True: green = fair die"
)
> for (i in 1:nSim) {
+ if (x$sim$states[i] == "Fair")
+ rect(i, -1, i + 1, 0, col = "green", border = NA)
+ else rect(i, -1, i + 1, 0, col = "red", border = NA)
+ }
> text(0, -3.2, adj = 0, cex = 0.8, col = "black", "Most probable path")
> for (i in 1:nSim) {
+ if (x$vit[i] == "Fair")
+ rect(i, -3, i + 1, -2, col = "green", border = NA)
+ else rect(i, -3, i + 1, -2, col = "red", border = NA)
+ }
> text(0, -5.2, adj = 0, cex = 0.8, col = "black", "Difference")
> differing = !(x$sim$states == x$vit)
> for (i in 1:nSim) {
+ if (differing[i])
+ rect(i, -5, i + 1, -4, col = rgb(0.3, 0.3, 0.3),
+ border = NA)
+ else rect(i, -5, i + 1, -4, col = rgb(0.9, 0.9, 0.9),
+ border = NA)
+ }
> points(x$posterior[2, ] - 3, type = "l")
> text(0, -7.2, adj = 0, cex = 0.8, col = "black", "Difference by posterior
-probability")
> differing = !(x$sim$states == x$vit)
> for (i in 1:nSim) {
+ if (posterior[1, i] > 0.5) {
+ if (x$sim$states[i] == "Fair")
+ rect(i, -7, i + 1, -6, col = rgb(0.9, 0.9, 0.9),
+ border = NA)
+ else rect(i, -7, i + 1, -6, col = rgb(0.3, 0.3, 0.3),
+ border = NA)
+ }
+ else {
+ if (x$sim$states[i] == "Unfair")
+ rect(i, -7, i + 1, -6, col = rgb(0.9, 0.9, 0.9),
+ border = NA)
+ else rect(i, -7, i + 1, -6, col = rgb(0.3, 0.3, 0.3),
+ border = NA)
+ }
+ }
>
Source :
R code for cut and paste¶
plot(x$sim$observation, ylim = c(-7.5, 6), pch = 3, main = mn,
xlab = xlb, ylab = ylb, bty = "n", yaxt = "n")
axis(2, at = 1:6)
#######Simulated, which die was used (truth)####################
text(0, -1.2, adj = 0, cex = 0.8, col = "black", "True: green = fair die")
for (i in 1:nSim) {
if (x$sim$states[i] == "Fair")
rect(i, -1, i + 1, 0, col = "green", border = NA)
else rect(i, -1, i + 1, 0, col = "red", border = NA)
}
########Most probable path (viterbi)#######################
text(0, -3.2, adj = 0, cex = 0.8, col = "black", "Most probable path")
for (i in 1:nSim) {
if (x$vit[i] == "Fair")
rect(i, -3, i + 1, -2, col = "green", border = NA)
else rect(i, -3, i + 1, -2, col = "red", border = NA)
}
##################Differences:
text(0, -5.2, adj = 0, cex = 0.8, col = "black", "Difference")
differing = !(x$sim$states == x$vit)
for (i in 1:nSim) {
if (differing[i])
rect(i, -5, i + 1, -4, col = rgb(0.3, 0.3, 0.3),
border = NA)
else rect(i, -5, i + 1, -4, col = rgb(0.9, 0.9, 0.9),
border = NA)
}
#################Posterior-probability:#########################
points(x$posterior[2, ] - 3, type = "l")
###############Difference with classification by posterior-probability:############
text(0, -7.2, adj = 0, cex = 0.8, col = "black", "Difference by posterior-probability")
differing = !(x$sim$states == x$vit)
for (i in 1:nSim) {
if (posterior[1, i] > 0.5) {
if (x$sim$states[i] == "Fair")
rect(i, -7, i + 1, -6, col = rgb(0.9, 0.9, 0.9),
border = NA)
else rect(i, -7, i + 1, -6, col = rgb(0.3, 0.3, 0.3),
border = NA)
}
else {
if (x$sim$states[i] == "Unfair")
rect(i, -7, i + 1, -6, col = rgb(0.9, 0.9, 0.9),
border = NA)
else rect(i, -7, i + 1, -6, col = rgb(0.3, 0.3, 0.3),
border = NA)
}
}
Table Of Contents
- Crash Course in Genomics
- Seeing the structure and the surprises
- Sequence Data are Strings
- Markov Chains
- Hidden Markov Models - the Unfair Casino
- Hidden Markov Model for CpG islands
- Underlying Algorithms
- PCA : Interpretation Examples
- PCA, SVD and MDS
- Binary Table/Contingency Table representation
- Binary Data and Graphs
- Modelling Mixtures: the Dirichlet distribution
- Gibbs Sampler Examples
- Microarrays
- HW1 Stats 366 - Stats 166
- Lab1 Reading and Manipulating genomes in R
- Lab2/Hw 2 Hidden Markov Models
- Lab3/Hw 3 Visualization and PCA
- Lab4 Networks
- Lab 5: Phylogenetic Trees and the Bootstrap
Search
Enter search terms or a module, class or function name.
