All-solid-state batteries have the potential to become high energy density and safe replacements for the commonly used liquid electrolyte Li-ion batteries. The considered solid electrolytes are not flammable in constrast to the liquids thus eliminating the security risks due to e.g. battery fires. Some solid electrolytes are electrochemically stable against lithium metal, opening up the possibility to replace graphitic intercalation anodes with lithium metal anodes, which would increase energy density.
Unlike the electrolytes used in solid oxide fuel cells, which require high temperatures for good conductivity, there are several so-called super-ionic solid Li-ion electrolytes, that have at least as high conductivities as the commonly used liquid electrolyte at moderate temperatures (with even better temperature ranges). However, only solid-state microbatteries are currently of practical use; solid-state batteries with high power density and long cycle life that could be used in electric vehicles have remained elusive. Given the good bulk conductivities of the electrolytes, interfacial issues between electrolyte and electrodes clearly play a role in the power density limitations of all-solid-state batteries [Luntz, Voss, Reuter, J. Phys. Chem. Lett. 6, 4599 (2015)].
Ideal Solid-solid Electrochemical Interfaces
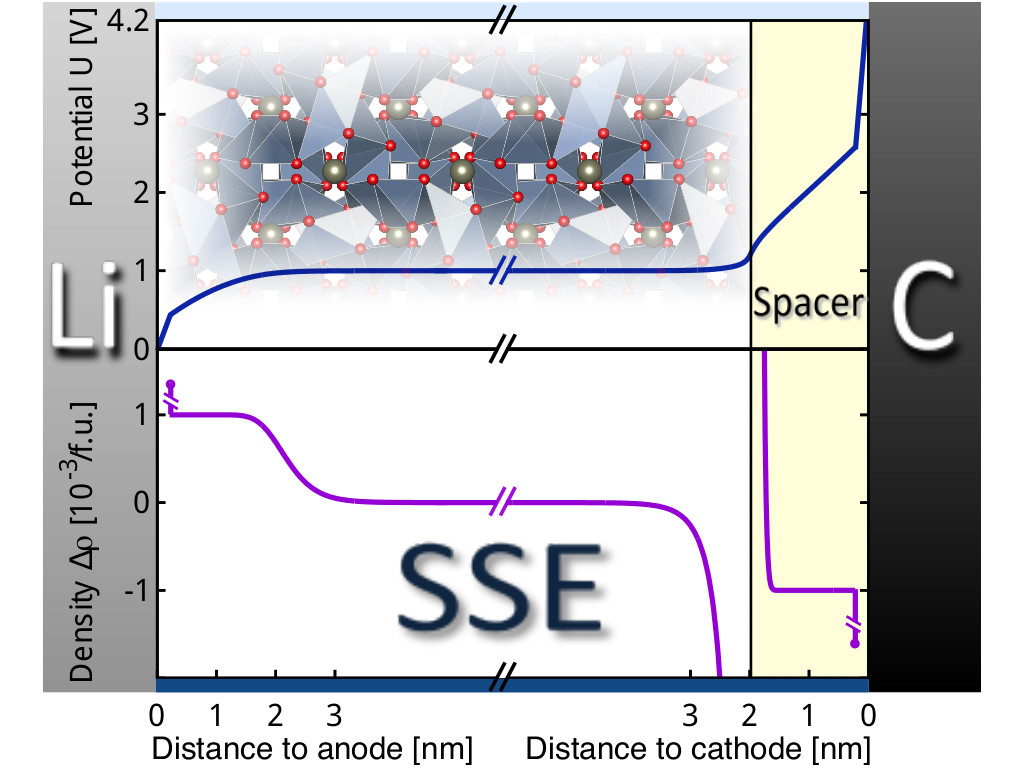
We consider sharp, ideal interfaces between the solid electrolyte and the electrodes. We neglect mechanical contact problems (that likely will occur during charge/discharge cycles) or complex interface morphology.
For the above figure, we have used a continuum modeling approach, where the discrete structure of the charge density with lattice sites is neglected and charge and potential are considered homogeneous parallel to the interface. The problem is thus reduced to one dimension. Anode and cathode simply are modeled as metallic electrostatic boundary conditions.
Density functional theory calculations can provide important parameters for modeling the electrolyte here: dielectric constant and the formation energies of charge-carrying Li defects. These formation energies govern what potential energy the carriers have in the bulk of the electrolyte (i.e. in sufficient distance to the electrodes). For electrolytes such as lithium lanthanum zirconate or lithium oxychloride, the typical formation energies of Li+ vacancies is about 1-1.5eV relative to Li metal. Most of the desirable open circuit battery voltage of 4-5eV will thus drop at the interface to the cathode (see figure above).
DFT Simulations of Ideal Solid-electrolyte Interfaces
The above continuum simulations with parameters typical for solid-state batteries (dielectric constant ~15, low carrier concentrations) suggest very thin charge double layers. We have performed density functional theory (DFT) simulations to investigate the double charge layers in more detail [Stegmaier, Voss, Reuter, Luntz, Chem. Mater. 29, 4330 (2017)]. The DFT calculations indeed indicate even thinner double layers consisting almost only out of the Helmholtz plane (the layer of charges closest to interface) and vanishing diffuse layer.
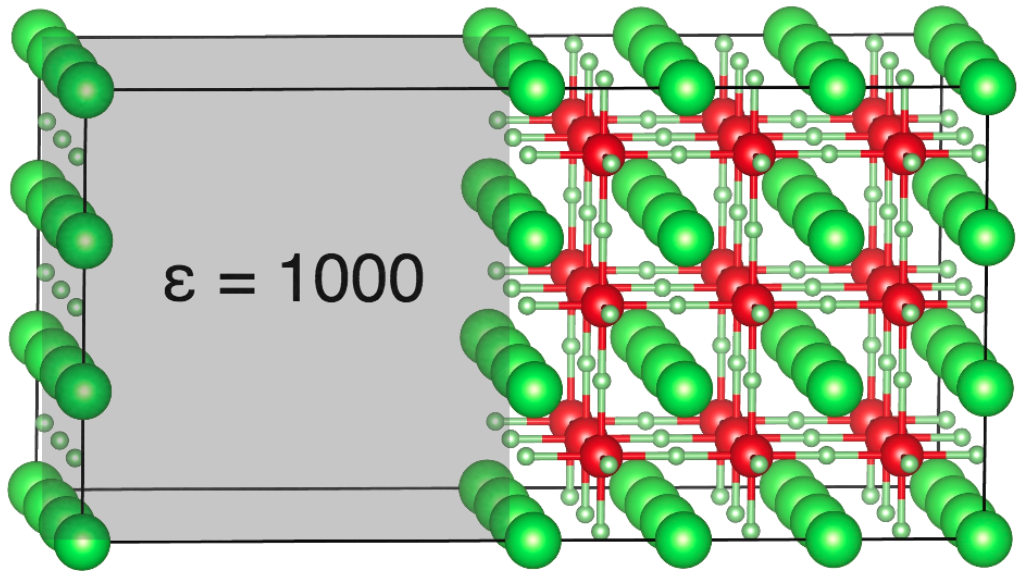
Rather than explicitly modeling an electrode|electrolyte interface, we only model the electrolyte quantum-mechanically within DFT (we have chosen Li3OCl as a representative case for a super-ionic electrolyte here). The electrode is modeled using a polarizable medium with very high dielectric constant (see figure above), so that electric fields are screened with image charges behaving similarly to an ideal metallic interface. We find that ionic relaxation screens the interaction between charge carriers so efficiently, that basically a whole plane of Li could be depleted. The strong image stabilization of carriers at the electrode interface outweighs vanishingly small carrier interactions. The limitation to carrier accumulation in the Helmholtz plane is entropy, which only becomes important here at carrier coverages approaching unity (see figure below).
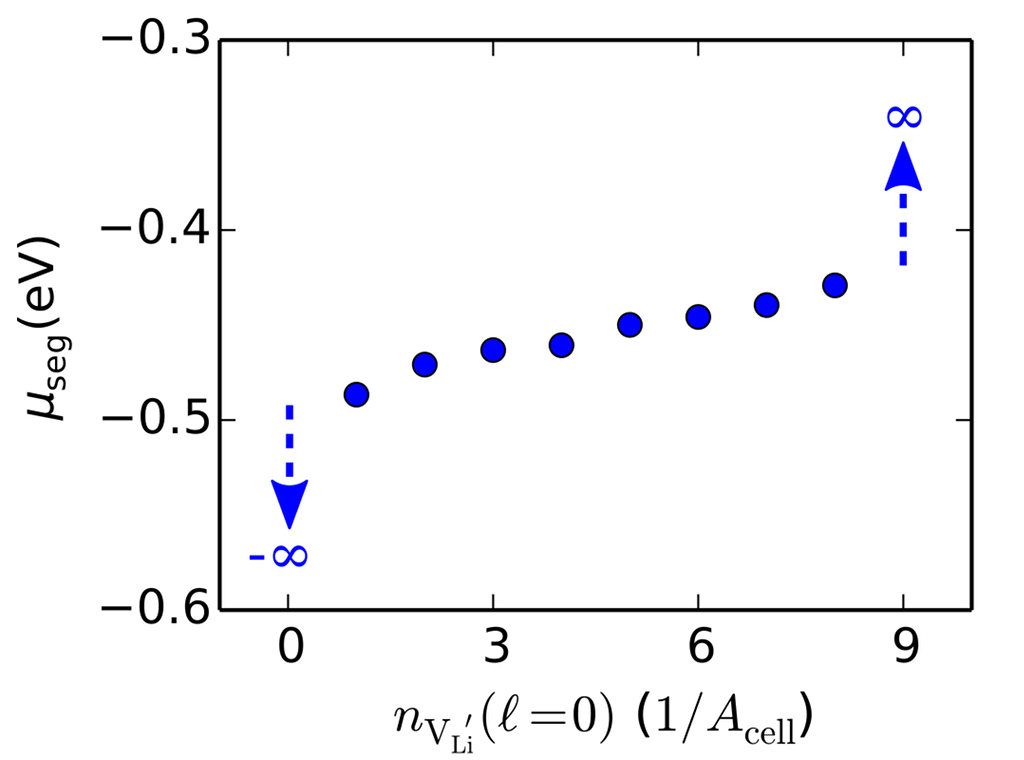
The simulations with the polarizable medium furthermore show that a depleted Helmholtz plane in Li3OCl could easily screen several Volts of potential drop (a result we expect to be generally true for similar solid ionic electrolytes). Since charge carrier interactions are limited to a single lattice spacing range due to effective ionic relaxation, accumulating significant amounts of charge in the Helmholtz plane is energetically feasible. We thus expect very thin charge double layers in solid-state batteries with strongly ionic electrolytes. Similar arguments hold for accumulation of positive charge (locally/intrinsically generated by strong negative potentials even in the case of vacancy mediated ion conduction) at the anode [Stegmaier, Voss, Reuter, Luntz, Chem. Mater. 29, 4330 (2017)].
Realistic interfaces will not be sharp, which can have an important effect on the double layers. More importantly, mechanical problems of electrolyte cracking by growing Li metal and contact problems pose considerable obstacles towards devising all-solid-state batteries with long cycle lifes and high power densities.
Ionic Diffusion in Glassy Solid Electrolytes
Modeling of ionic diffusion in glassy electrolytes and glassy systems in general requires sufficient statistical sampling using sufficiently large supercells, which generally renders first-principles approaches unfeasible. Only consisting of low atomic number elements, Li3OCl lends itself to be studied with force fields, enabling access to sufficiently long timescales.
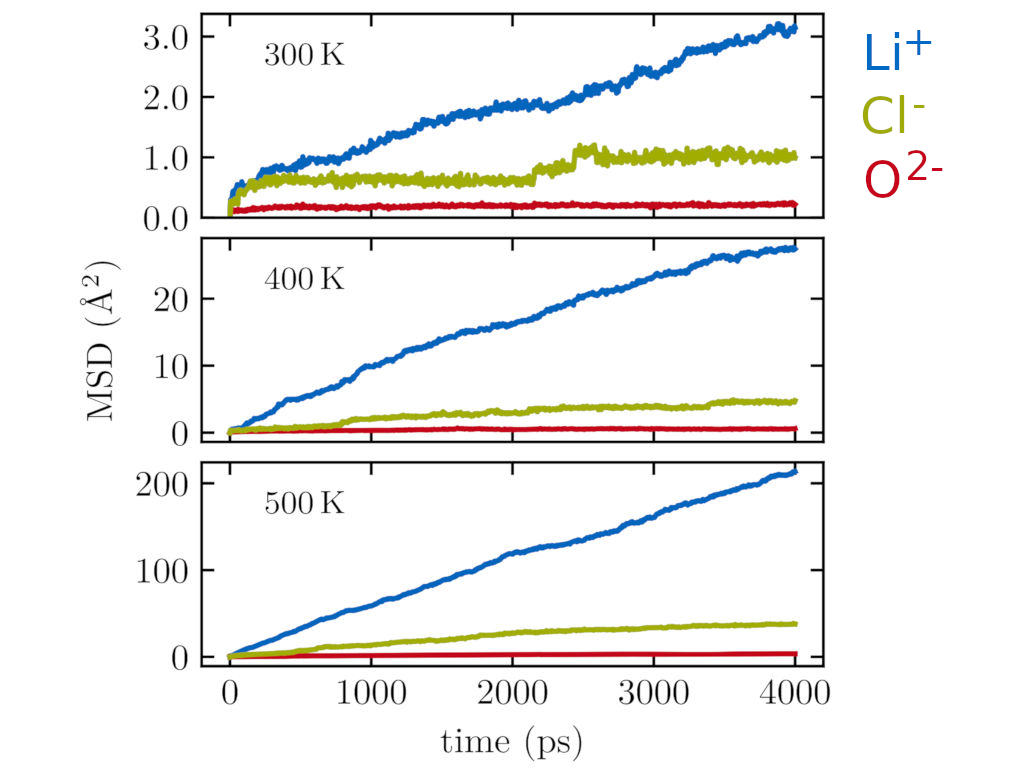
Interestingly, using such force field molecular dynamics, we find that not only Li+ ions are mobile, but also to some extent Cl-. The picture of a solid-state electrolyte as a single-ion conductor with only one mobile species is thus too simple here. Similar (unwanted) counter-ion mobility could also exist in other ionic electrolytes.