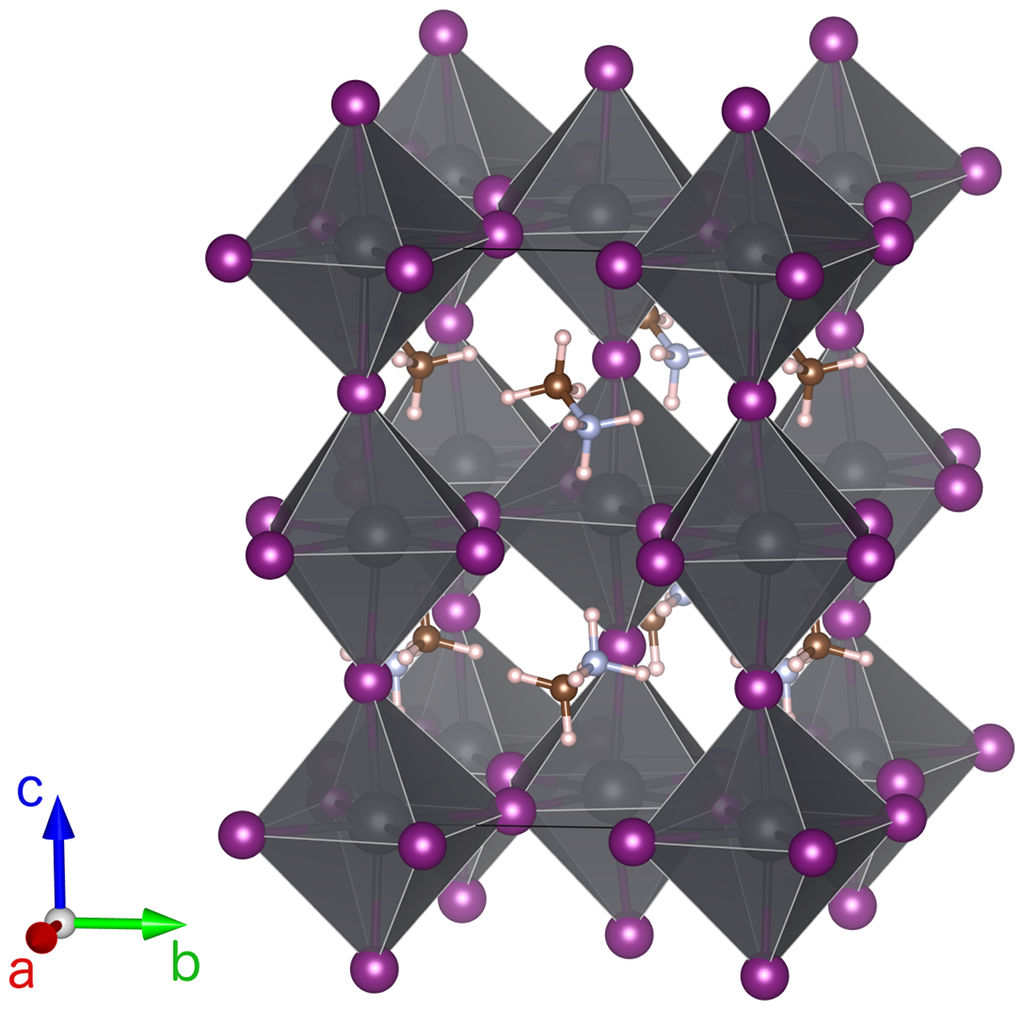
Mixed organic/inorganic perovskites are promising materials as light absorbers for photovoltaic applications. Due to the large sizes of the organic cations, structures with large anions such as iodine with lead as central metal ion can be stabilized. The resulting large lattice constants and interatomic distances lead to relatively low orbital overlap and hence to smaller band gaps than typical for complex oxides or halides. Indeed, methylammonium lead iodide MAPbI3 has an almost ideal (for the adsorption of the solar spectrum with a single junction cell) band gap of about 1.7eV. Moreover, MAPbI3 can be synthesized relatively easily, and likely point defects only seem to introduce shallow defect states.
Theory
From a computational point of view, mixed organic/inorganic perovskites pose the challenge of structural complexity as the organic cations are not spherically symmetric and can either form patterns of orientations or be disordered. Another challenge in addition to the inherent band gap problems of DFT is the importance of strong spin-orbit coupling (SOC) due to the lead (but also the iodine) ions. GW quasiparticle spectra calculations are significantly more expensive than DFT bandstructure calculations, and the requirement to work with spinor wavefunctions to deal with SOC increases the computational effort further.
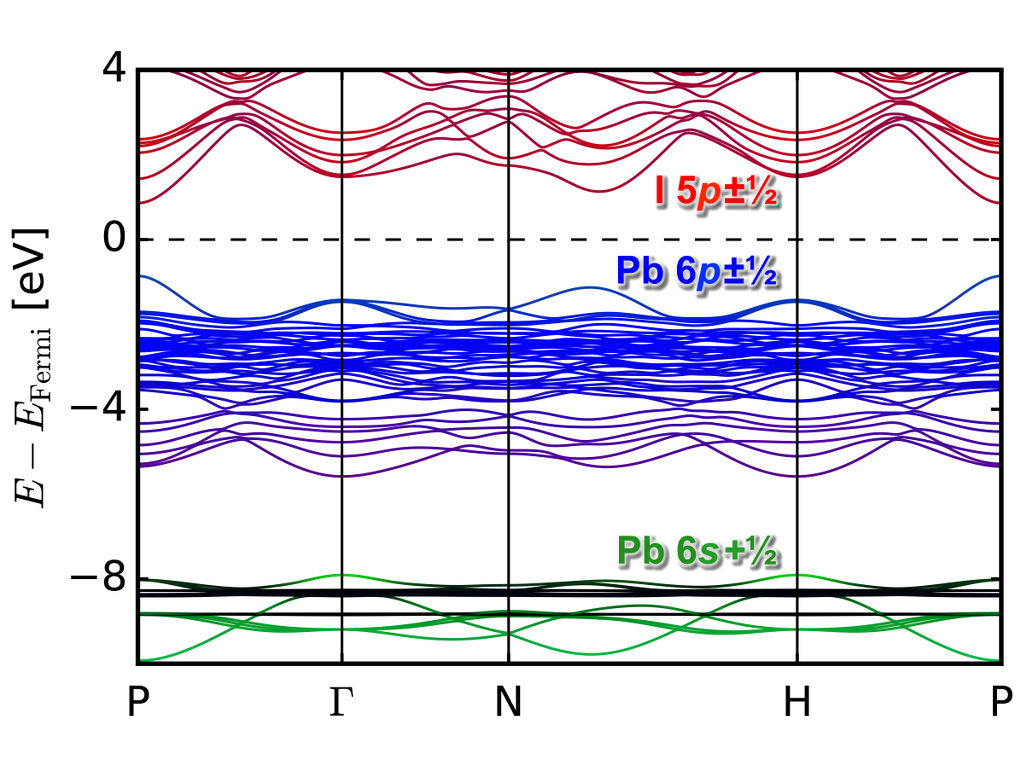
To accelerate the band gap calculations, we have implemented an orbital dependent functional with quasiparticle corrections to the DFT bandstructure in the Quantum Espresso code (which can account for spin-orbit interactions using pseudopotentials with $j$-dependent projectors). The functional (GLLBsc) was divised by Kuisma and others [Phys. Rev. B 82, 115106 (2010)], who have modified the GLLB functional [Gritsenko et al., Phys. Rev. A 51, 1944 (1995)] to calculate derivative-discontinuity corrections to the Kohn-Sham band gaps of semiconductors and insulators. This method allows for band gap predictions with a computational complexity of that of a standard DFT groundstate calculation. In combination with the implementation of SOC in Quantum Espresso, we are able to calculate band gaps for mixed organic/inorganic perovskite with relativistic effects efficiently. Below is shown the GLLBsc bandstructure of MaPb3 under pressure.
Comparison to Experiment
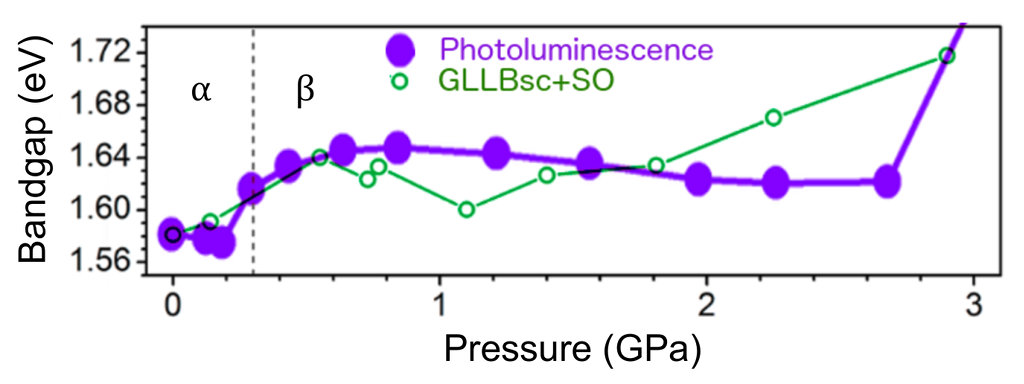
Considering both relativistic effects (resulting in a band gap reduction for these materials) and the derivative-discontinuity corrections (which increase the otherwise underestimated DFT band gaps), the agreement between experiment and theory is relatively good (see figure above). The GLLBsc calculations capture the overall trend in band gap dependence on pressure: the increase in band gap accompanying the crystallographic phase transition from the $\alpha$- to the $\beta$-phase and the overall band gap increase for higher pressures [Jaffe et al., ACS Cent. Sci. 2, 201 (2016)].
An increase in band gap is desirable, as the optimum single-junction band gap is about ~1.8eV. Another approach to increase the gap is ionic substitution.