In density functional theory (DFT), the (typically) most important energetic contributions are accounted for by the kinetic energy $\mathit{T}$$\textrm{non-int.}$ of a fictitious non-interacting system and electrostatic interactions $E_\textrm{estat}$ of the electrons with their charge density and with the nuclear cores:
$$E_\textrm{electronic} = T _\textrm{non-int.} + E _\textrm{estat} + E _\textrm{xc} .$$
The total energy of the system includes additionally the electrostatic repulsion between the nuclear cores. Using the Born-Oppenheimer approximation, the positions of the nuclear cores are parameters of the electronic Hamiltonian thus defining a potential energy surface. The electronic system is assumed to adiabatically follow changes in the nuclear coordinates relaxing to its groundstate on much faster timescales than the timescales of nuclear motion (electron-phonon coupling, e.g., is a correction to this adiabatic approximation).
The exchange-correlation energy $\mathit{E}$$\textrm{xc}$ accounts for the remaining electronic energy not included in the non-interacting kinetic and electrostatic terms. To calculate the non-interacting kinetic energy $\mathit{T}$$\textrm{non-int.}$, an effective potential is needed which the fictitious particles are exposed to. The electrostatic interaction terms are accounted for by the corresponding electrostatic potentials, and $\mathit{E}$$\textrm{xc}$ by the exchange correlation potential
$$V _\textrm{xc}(\textbf{r}) = \frac{\delta E _\textrm{xc}(\textbf{r})}{\delta \rho(\textbf{r})} .$$
The exact form of $\mathit{E}$$\textrm{xc}$ is not known: approximations have to be made. The simplest approximations are so-called semi-local exchange-correlation functionals, since these functionals only dependent locally on the electronic charge density $\rho(\textbf{r})$ and its gradient $\textbf{∇} \rho(\textbf{r})$. The most basic functional is the local density approximation (LDA), where $\mathit{E}$$\textrm{xc}$$(\textbf{r})$ is approximated point by point in real space by the exchange-correlation energy of the homogeneous electron gas of density $\rho(\textbf{r})$. The exchange energy $E_\textrm{x}^\textrm{hom}\sim\rho^{4 / 3}(\textbf{r})$ and the correlation energy can be expressed as a numerical extrapolation of analytical low and high density limits and quantum Monte Carlo results for intermediate homogeneous densities [Perdew and Zunger, Phys. Rev. B 23, 5048 (1981); Ceperley and Alder, Phys. Rev. Lett. 45, 566 (1980)]. When making density-gradient corrections to the LDA, it has proven crucial to maintain the correct sum of the exchange-correlation hole which should amount to one electron missing in any hole independent of the distance to the other particle seeing the hole. Perdew has shown [Phys. Rev. Lett. 55, 1665 (1985)] that a realspace cutoff in the density gradient expansion can be employed to fulfill this rule leading to a general form of the gradient-corrected exchange energy of
$$E _\textrm{x} = \int \textrm{d}^3 r E _\textrm{x}^\textrm{hom} [\rho(\textbf{r})] \cdot f _\textrm{x}(s(\textbf{r})) .$$
The so-called exchange enhancement $f _\textrm{x}$ does not explicitly depend on the density nor its gradient but only implicitly through the reduced density gradient
$$ s(\textbf{r}) = \frac{|\textbf{∇} \rho(\textbf{r})|}{2 k _\textrm{F}(\textbf{r}) \rho(\textbf{r})} ,$$
with the Fermi wave vector $k _\textrm{F}(\textbf{r}) = \sqrt[3]{3 \pi^2 \rho(\textbf{r})}$.
When $\mathit{T}$$\textrm{non-int.}$ and $E_\textrm{estat}$ account for most of the electronic energy and $\mathit{E}$$\textrm{xc}$ is only a relatively small correction, the LDA and generalized-gradient approximations (GGA) perform very well in predicting structural properties and total energetics. If Coulomb interactions are strong, competing with kinetic terms, beyond density functional corrections become necessary.
Semi-empirical Functionals
We devise exchange-correlation functionals by fitting the functional form against higher-level of theory data (e.g. wave function method results for gas phase chemistry) and experimental benchmark data for bulk cohesive and elastic properties and surface chemistry. Instructions on how to use our implementations can be found at this link.
For the MCML (multi-purpose, constrained, and machine-learned) functional [https://doi.org/10.1002/jcc.26732], we have focused on training the semi-local exchange part in a meta-generalized-gradient approximation (meta-GGA), keeping the correlation part in GGA form. In meta-GGAs, the functional is not only parameterized with respect to the charge density and its gradient, but also with respect to the Kohn-Sham kinetic energy density. This extension allows for suppression of one-electron self-interaction errors (e.g. the spurious Hartree energy in the DFT description of the hydrogen atom can be cancelled). Generally, from this non-interacting kinetic energy density, the local bonding character can be detected, and meta-GGAs can thus provide simultaneously better performance for e.g. reaction energies and lattice properties, while GGAs typically perform well either only for the former or the latter.
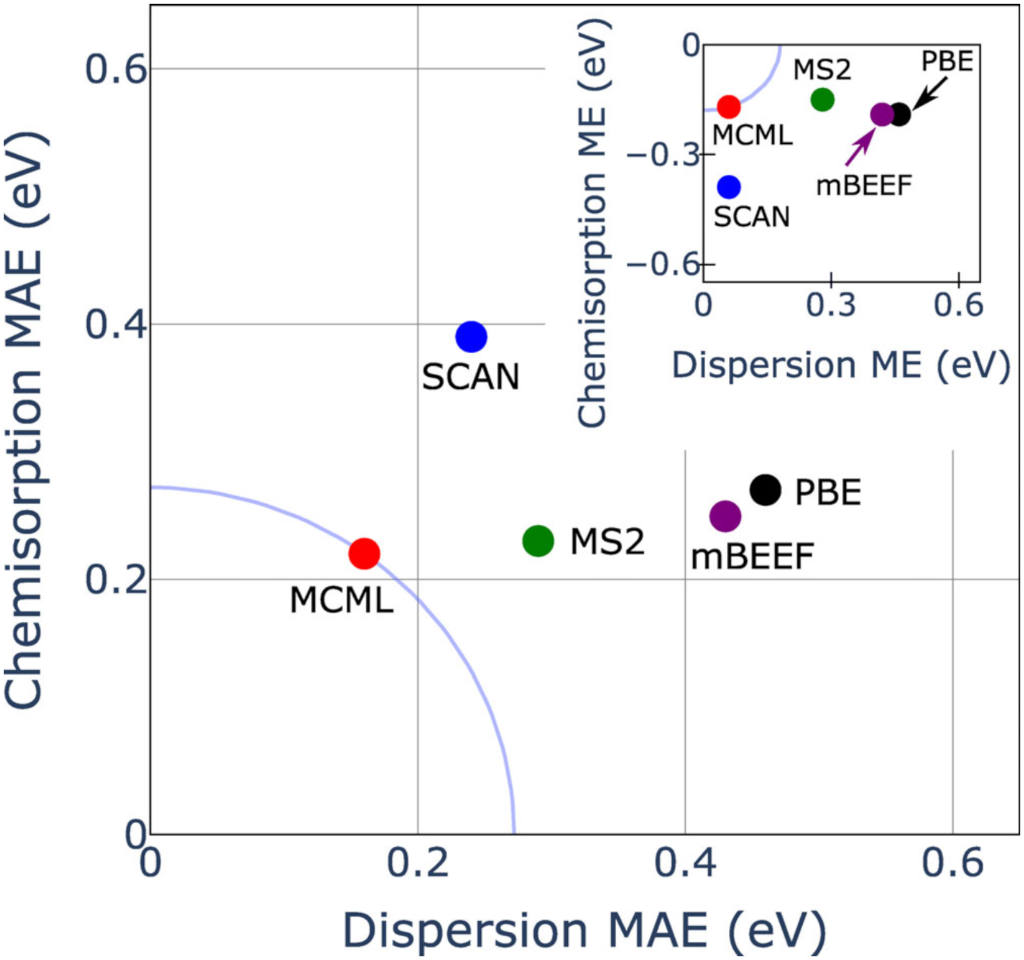
We furthermore optimize meta-GGA+vdW functionals, where we simultaneously optimize the semi-local exchange and a non-local vdW part. The resulting functional VCML-rVV10 [https://doi.org/10.1002/jcc.26872] shows improved description of dispersion energetics. The evaluation of density-dependent vdW-kernels comes at (moderate) extra cost in DFT simulations, but we recommend the usage of VCML-rVV10 over MCML (both optimized for surface chemistry and bulk properties), if an accurate description of vdW forces is important.
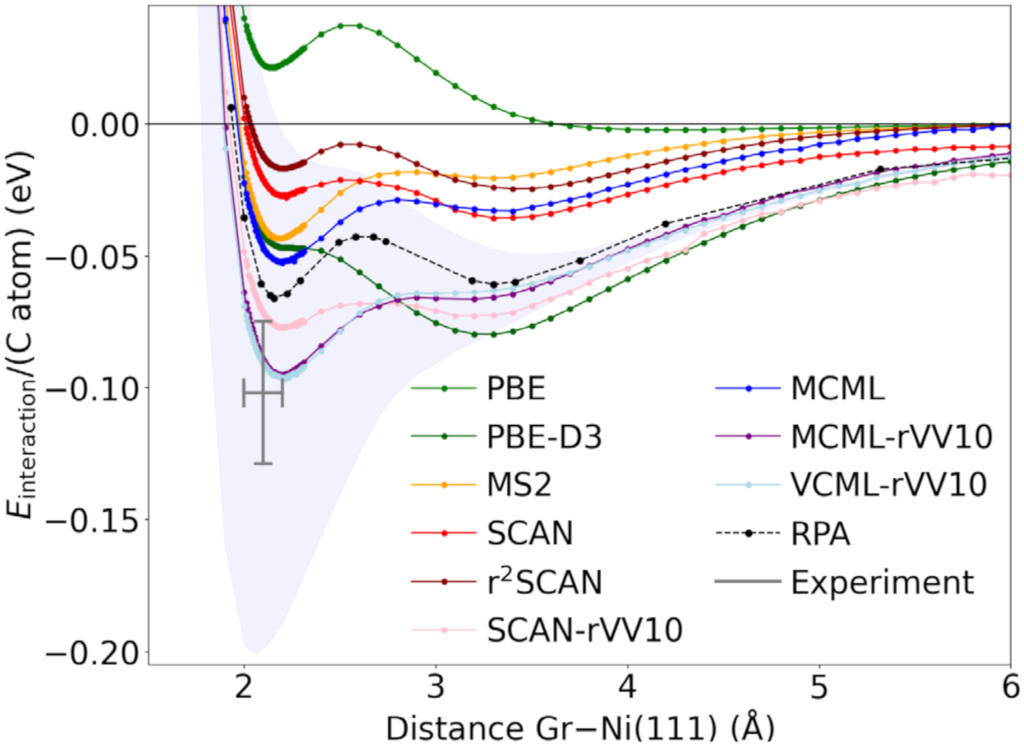
With help of the minimized cost function for the functional optimization, we can randomly draw enhancement factors (see figure on interaction of graphene with nickel below) which can be used to infer the uncertainty on computed total energy differences based on Bayesian statistics. The total energy uncertainties can be computed efficiently keeping the charge (and Kohn-Sham kinetic energy) density fixed at its solution according to the optimal fit of the functional. This approach allows for an approximate quantification of the uncertainty in the computed predictions due to uncertainty in the functional form of the density functional approximation to exchange and correlation.
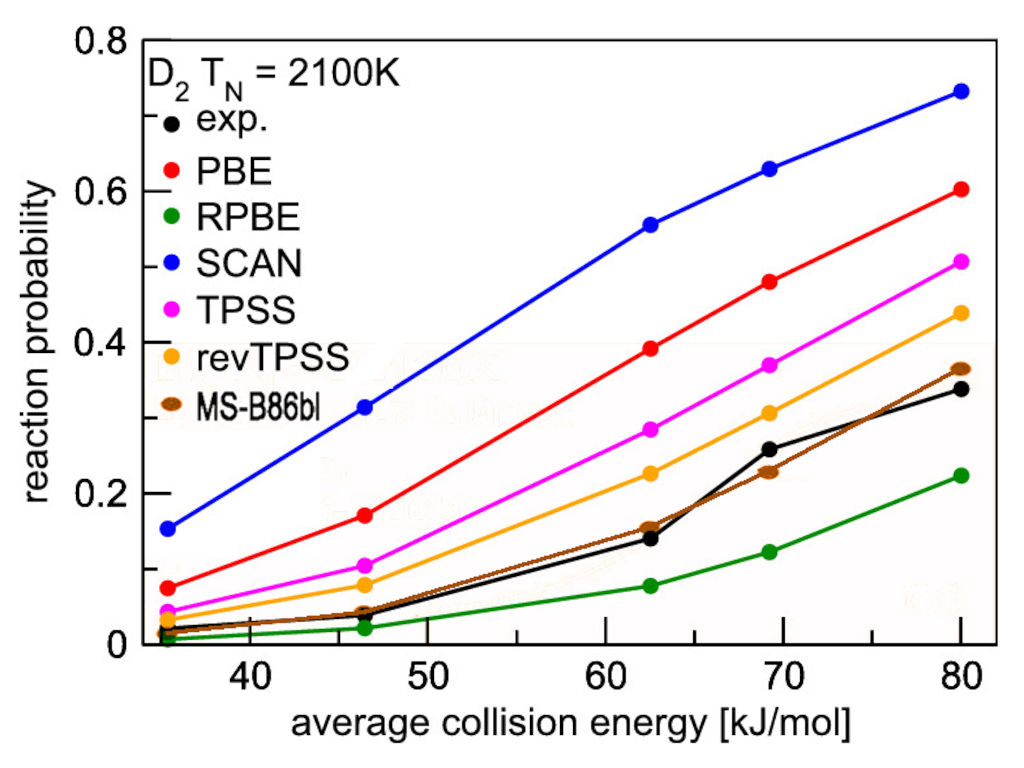
Also less complex models for the exchange enhancement factors than the ones above can be simultaneously optimized for bulk elastic and surface chemistry predictions by interpolating between two PBE-like GGAs, giving more weight to a GGA well-suited for bulk properties when the kinetic energy density approaches that of the homogeneous electron gas. The figure below shows the performance of such an optimized meta GGA [Smeets, Voss, Kroes, J. Phys. Chem. A 123, 5395 (2019)] in predicting surface reaction probabilities.
In general, significant self-interaction errors (present e.g. in transition metal oxides with localized $d$- or $f$-states) require a beyond density functional treatment. Our current work in this field consists of developments in local density matrix occupation-dependent functionals (GGA+U), where we use machine learning to enable the usage of these approaches with site- and reaction coordinate-dependent U-parameters for surface reactions [Voss, J. Phys. Commun. 6, 035009 (2022)].