Research description:
|
The main focus of my work is Floer homology and its
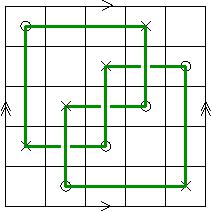
applications to topology. Floer homology is a construction that can be used to study 3-dimensional manifolds and 4-dimensional cobordisms between them. One variant of Floer homology is defined starting from the Seiberg-Witten equations. In an indirect way, this construction can also be used to understand the triangulations of manifolds of dimension greater than 4. In 2013, I used it to show that there exist non-triangulable manifolds in these dimensions. Here is a short description of this work that I wrote for the UCLA Math Newsletter. More details can be found in this expository paper on The Conley index, gauge theory, and triangulations. The Simons Center site has a video of a talk I gave there in May 2013. Another version of Floer homology is Heegaard Floer homology, which was developed by Peter Ozsváth and Zoltán Szabó. In joint work with several collaborators, we found that Heegaard Floer homology (and the related invariants of knots, links, and four-manifolds) can be described combinatorially. A key ingredient in these descriptions was the use of grid diagrams for knots. An example of a grid diagram (representing the trefoil knot) is shown in the figure on the right. To learn more about this subject, here is a survey paper on Grid diagrams in Heegaard Floer theory, a video of a talk I gave at MSRI in March 2010, as well as the slides of a colloquium talk. I have also done research on other aspects of Floer homology, such as:
My research is currently supported by a Simons Investigator Award and a Simons Collaboration Grant on New Structures in Low-Dimensional Topology. |
|