Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers

S. Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein

Foundations and Trends in Machine Learning, 3(1):1–122, 2011. (Original draft posted November 2010.)

Many problems of recent interest in statistics and machine learning can be posed in the framework of convex optimization. Due to the explosion in size and complexity of modern datasets, it is increasingly important to be able to solve problems with a very large number of features, training examples, or both. As a result, both the decentralized collection or storage of these datasets as well as accompanying distributed solution methods are either necessary or at least highly desirable. In this paper, we argue that the alternating direction method of multipliers is well suited to distributed convex optimization, and in particular to large-scale problems arising in statistics, machine learning, and related areas. The method was developed in the 1970s, with roots in the 1950s, and is equivalent or closely related to many other algorithms, such as dual decomposition, the method of multipliers, Douglas-Rachford splitting, Spingarn's method of partial inverses, Dykstra's alternating projections, Bregman iterative algorithms for 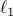ell_1 problems, proximal methods, and others. After briefly surveying the theory and history of the algorithm, we discuss applications to a wide variety of statistical and machine learning problems of recent interest, including the lasso, sparse logistic regression, basis pursuit, covariance selection, support vector machines, and many others. We also discuss general distributed optimization, extensions to the nonconvex setting, and efficient implementation, including some details on distributed MPI and Hadoop MapReduce implementations.

Talks:

Stanford Statistics department
EE 364b lecture (longer and more recent)
NIPS Optimization workshop (video)

Related papers: