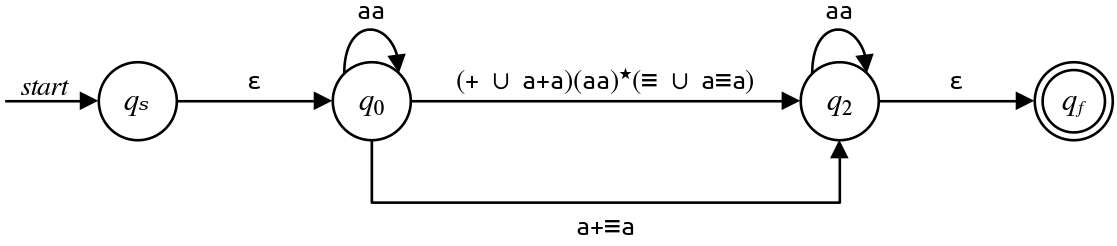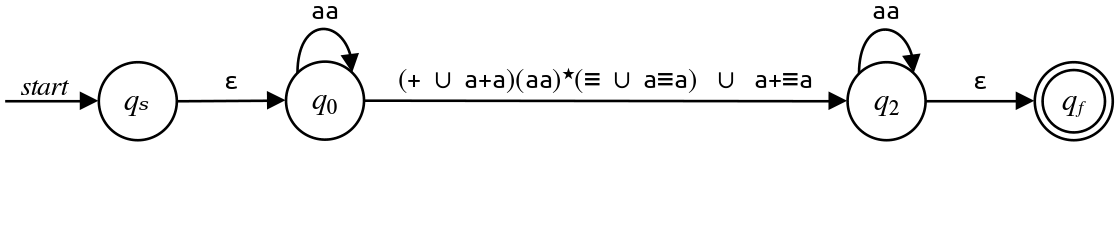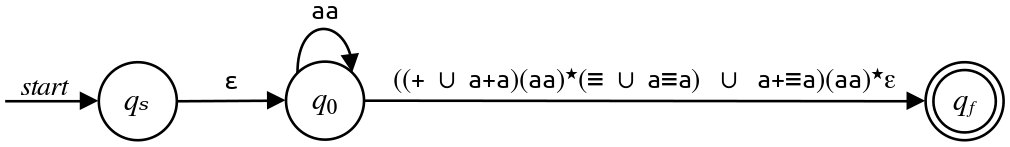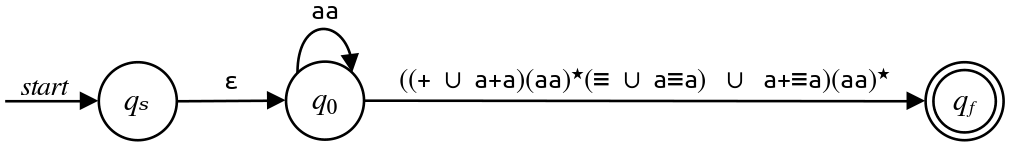Guide to State Elimination

Dear Mr. President: There are too many states nowadays. Please eliminate three. I am not a crackpot! (The Simpsons)

The state elimination algorithm transforms a DFA or NFA into regular expression. This is a big deal in Theoryland, as it shows that there's nothing you can do with DFA or NFA that you can't do with a regex. In practice, it's a useful tool to keep in your toolkit when designing regexes. While it probably shouldn't be your first line of attack when crafting regular expressions (the Guide to Regular Expressions outlines some techniques that are usually more effective), every now and then the state elimination algorithm ends up being one of the easiest ways to write a regex for a language.

In lecture, we did an example of the state elimination algorithm, which showed off the main technique. There's also a slide that details the full workings of how to do state elimination. This guide presents a further example of how to do state elimination so that the algorithm becomes easier to understand.

Example: Addition Parity

Let's begin with the following language $L$ over $\Sigma = \mathtt{\set{a, +, \equiv}}\text:$

\[L = \set{\mathtt{a}^m + \mathtt{a}^n \equiv \mathtt{a}^p \suchthat m, n, p \in \naturals \ \land \ m + n \equiv_2 p }\text.\]

So, for example, we have $\mathtt{aaa+aaa \equiv aaaaaa} \in L$ because there are three a's in the first group, three as in the second group, six a's in the third group, and it's true that $3 + 3 \equiv_2 6\text.$ We also have $\mathtt{aa+aaaa \equiv aa} \in L\text,$ since there are two a's in the first group, four a's in the second group, and two a's in the third group, and $2 + 4 \equiv_2 2\text.$ More generally, the format of the strings in the language is a group of a's of length $m$, a plus sign, then a second group of a's of length $n$, then an $\equiv$ symbol, and a third group of a's of length $p$ such that $m + n$ and $p$ have the same parity (they're either both even or both odd). Note that $+\equiv$ is also in the language (zero a's in each group), as are $\mathtt{a}+\equiv\mathtt{a}$ and $+\mathtt{a}\equiv\mathtt{a}\text.$

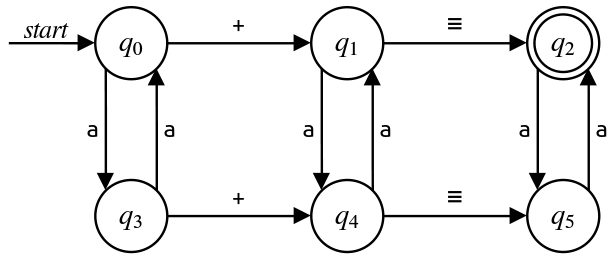
It's a worthwhile but challenging exercise to try to design a regex for this language given nothing more than the above. But let's suppose that, for some reason, you were getting stuck doing so and you weren't sure how to proceed. Your next line of attack might then be to design an NFA for this language and use the state elimination algorithm to turn that NFA into a regex. Here's one possible NFA for this language:

Before moving on, let's take a minute to see how this automaton works. Since all that matters to the language is the parity (evenness/oddness) of the counts of the as, the automaton consists of two parallel rows of states. On the top are states $q_0\text,$ $q_1\text,$ and $q_2\text,$ which corresponding to being in the first, second, and third groups of a's. On the bottom are $q_3\text,$ $q_4\text,$ and $q_5\text,$ which similarly track which group we're in. The transitions vertically between the two halves corresponding to changing the parity of the total number of a's read thus far. Every time we see an a in the top (even) set of states, we move to the bottom (odd) set of states and vice-versa.

Our goal is to turn this NFA into a regular expression for $L$ using the state elimination algorithm.

Initial Setup

We begin with the first step of the algorithm:

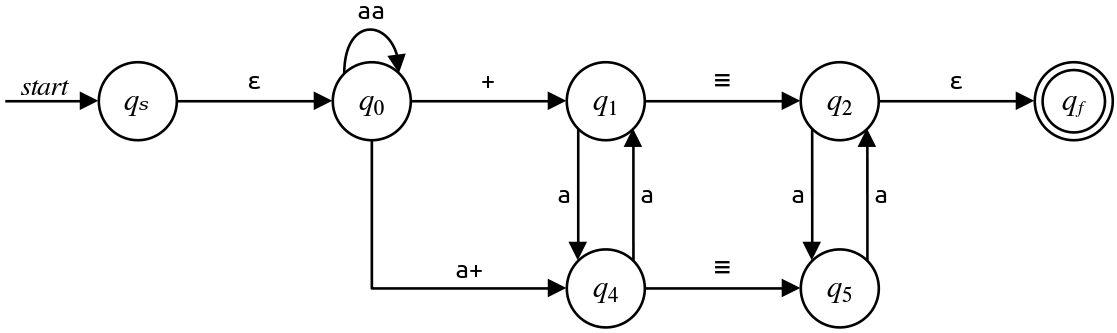
Step One: Add in a new start state $q_s$ with a $\varepsilon$ transition to the old start state. Add in a new accepting state $q_f$ and add $\varepsilon$ transitions from each old accepting state to $q_f\text.$ Finally, make only $q_f$ the accepting state.

The purpose of this step is to set us up for success later on. We will ultimately remove all states in the automaton besides $q_s$ and $q_f\text,$ and when we're done, the transition from $q_s$ to $q_f$ will consist of the regular expression we want.

After doing this, we get the following automaton:

We next proceed to step two of the algorithm - which is the real meat of the algorithm:

Step Two: Eliminate all states from the NFA other than $q_s$ and $q_f\text.$ To eliminate a state $q_{gone}\text,$ do the following:

Find all pairs of states $(q_{in}, q_{out})$ where $q_{in}$ has a transition to $q_{gone}\text,$ where $q_{gone}$ has a transition to $q_{out}\text,$ and where neither $q_{in}$ or $q_{out}$ is $q_{gone}\text.$
For each pair $(q_{in}, q_{out})\text,$ add a transition directly from $q_{in}$ to $q_{out}\text.$ Label that transition with a regex simulating the effect of transitioning from $q_{in}$ to $q_{gone}\text,$ following any self-loops on $q_{gone}\text,$ then transitioning to $q_{out}\text.$ (Details below.)
Remove $q_{gone}$ from the automaton.
Consolidate parallel transitions. (Details below.)
(Optional) Simplify any complex regexes that arise in the process.

There is no requirement about which state we eliminate first or the order in which we eliminate the states. Any choice will work. However, some choices may work much, much better than others. It's something you pick up by feel as you get more comfortable with the algorithm. I've scouted this particular example out and found it easiest to begin by removing $q_3$ first, so that's where we'll begin.

Eliminating $q_3$

Our first task in eliminating $q_3$ is to find all pairs of states $(q_{in}, q_{out})$ where $q_{in}$ transitions into $q_3$ and $q_3$ transitions into $q_{out}\text.$ Looking at the automaton, we see that only one other state $(q_0)$ has a transition into $q_3\text,$ and that $q_3$ has transitions into two other states $(q_0\text{ and } q_4\text{).}$ This means that there are two pairs of states for us to look at: $(q_0, q_0)$ and $(q_0, q_4)\text.$

The next step is to add new transitions into the automaton, one for each pair. We'll thus add a transition from $q_0$ to itself and a transition from $q_0$ to $q_4\text.$

What should go on these transitions? Let's begin with the new transition from $q_0$ to $q_4\text.$ This new transition is designed to simulate the effect of taking the transition from $q_0$ to $q_3$ and from $q_3$ to $q_4\text.$ The transition from $q_0$ to $q_3$ is an a transition, and the transition from $q_3$ to $q_4$ is a + transition, so we'll label this transition a+. (It's a slightly unfortunate choice of alphabet that we have + in this regex meaning "the character +" rather than "the Kleene plus operation." In retrospect, it would have been better to use a different symbol here, but + feels natural in the context of the language, so we'll just roll with it for this example.)

Similarly, let's look at the new transition we need to add from $q_0$ to itself. This should simulate the effect of going from $q_0$ to $q_3\text,$ then from $q_3$ back to $q_0\text.$ The transition from $q_0$ to $q_3$ is labeled a and the transition from $q_3$ to $q_0$ is labeled a, so the new transition will be labeled aa.

Here's a summary of the new transitions:

\[\begin{array}{c|c|c} \text{In} & \text{Out} & \text{Regex} \\ \hline q_0 & q_4 & \mathtt{a+} \\ q_0 & q_0 & \mathtt{aa} \end{array}\]

Now that we know what the new transitions are, we will remove $q_3$ by adding in these new transitions, then deleting $q_3$ from the automaton. The result is shown here:

We now have one fewer state in our automaton. If we look at the rest of what we need to do to eliminate this state (consolidate parallel transitions and simplify regexes), we find that neither applies: there are no parallel transitions, and the regexes we have here are already as simple as possible. So let's move on to remove our next state.

Eliminating $q_5$

Let's next remove $q_5\text.$ We begin, as before, by finding all other states with transitions into $q_5$ and all other states that $q_5$ transitions into. $q_5$ has two incoming transitions (one from $q_4$ and one from $q_2\text)$ and one outgoing transition (to $q_2\text{).}$ We therefore will need to fill in the following table:

\[\begin{array}{c|c|c} \text{In} & \text{Out} & \text{Regex} \\ \hline q_4 & q_2 & \blank \\ q_2 & q_2 & \blank \end{array}\]

Let's begin with the transition that will go from $q_4$ to $q_2\text.$ As before, the idea is to simulate going from $q_4$ to $q_5$ and then from $q_5$ to $q_2\text.$ The transition from $q_4$ to $q_5$ is labeled $\mathtt{\equiv}$ and the transition from $q_5$ to $q_2$ is labeled a, so this regex will be labeled $\mathtt{\equiv a}\text.$

Next, let's look at the transition from $q_2$ back to itself. This transition simulates going from $q_2$ to $q_5$ and then from $q_5$ to $q_2\text.$ Those transitions are each labeled with a, so the new transition gets the label aa. We've thus filled in our table:

\[\begin{array}{c|c|c} \text{In} & \text{Out} & \text{Regex} \\ \hline q_4 & q_2 & \mathtt{\equiv a} \\ q_2 & q_2 & \mathtt{aa} \end{array}\]

And we can update our automaton by removing $q_5$ and adding these new transitions in, as shown here:

You might notice a general pattern here for how we decide what goes on the transition. Specifically:

When eliminating state $q_{gone}$ and adding a transition from $q_{in}$ to $q_{out}\text,$ where $q_{gone}$ has no self-loops, determine the label on the transition as follows:

Let $R_{in}$ be the regex on the transition from $q_{in}$ to $q_{gone}\text.$
Let $R_{out}$ be the regex on the transition from $q_{gone}$ to $q_{out}\text.$
The resulting regex on the transition from $q_{in}$ to $q_{out}$ is $\left(R_{in}\right)\left(R_{out}\right)\text,$ where the parentheses may be omitted if they don't change the meaning of the resulting regex.

The idea is to simulate entering the state and then leaving, hence the transition label.

Eliminating $q_4$

Let's now eliminate $q_4\text.$ This one is a bit more complex because there are more incoming and outgoing transitions, but it's not too bad. We end up needing to fill in this table:

\[\begin{array}{c|c|c} \text{In} & \text{Out} & \text{Regex} \\ \hline q_0 & q_2 & \blank \\ q_0 & q_1 & \blank \\ q_1 & q_2 & \blank \\ q_1 & q_1 & \blank \\ \end{array}\]

Using the information from the box above, we can determine the transitions like this:

$q_0$ to $q_2\text:$ The transition from $q_0$ to $q_4$ is labeled a+ and the transition from $q_4$ to $q_2$ is labeled $\mathtt{\equiv a}\text,$ so our new transition is labeled $\mathtt{a + \equiv a}\text.$
$q_0$ to $q_1\text:$ The transition from $q_0$ to $q_4$ is labeled a+ and the transition from $q_4$ to $q_1$ is labeled $\mathtt{a}\text,$ so our new transition is labeled $\mathtt{a+a}\text.$
$q_1$ to $q_2\text:$ The transition from $q_1$ to $q_4$ is labele a and the transition from $q_4$ to $q_2$ is labeled $\mathtt{\equiv a}\text,$ so our new transition is labeled $\mathtt{a \equiv a}\text.$
$q_1$ to $q_1\text:$ The transition from $q_1$ to $q_4$ is labele a and the transition from $q_4$ to $q_1$ is labeled $\mathtt{a}\text,$ so our new transition is labeled $\mathtt{aa}\text.$

We therefore fill in our table like this:

\[\begin{array}{c|c|c} \text{In} & \text{Out} & \text{Regex} \\ \hline q_0 & q_2 & \mathtt{a + \equiv a}\\ q_0 & q_1 & \mathtt{a + a}\\ q_1 & q_2 & \mathtt{a \equiv a} \\ q_1 & q_1 & \mathtt{aa}\\ \end{array}\]

We can then introduce those transitions into our automaton, and remove $q_4\text,$ to get the following:

At this point, we have a little bit more work to do. There are two parallel transitions between $q_0$ and $q_1$ and between $q1$ and $q_2\text.$ We will need to consolidate these together.

Intuitively, you can think of these two parallel transitions as saying "there are two separate ways to transition between these states." We need to have a single transition between them, which we can create by taking the union of the regexes on the parallel transitions. That way, we can simulate the effect of taking the top transition by taking the first option in the regex, and we can simulate the effect of taking the bottom transition by taking the second option in the regex.

This is shown here:

Eliminating $q_1$

Let's now eliminate $q_1$ from this automaton. As before, we start with a table of in/out pairs, which is fairly short this time:

\[\begin{array}{c|c|c} \text{In} & \text{Out} & \text{Regex} \\ \hline q_0 & q_2 & \blank \end{array}\]

The procedure for determining what goes on this transition is different than for the previous cases because $q_1$ has a transition back to itself. As before, we want to simulate with the new $q_0$ to $q_2$ transition the effect of entering $q_1$ from $q_0$ and then proceeding to $q_2\text.$ However, we also need to account for the possibility that, once we're at $q_1\text,$ we take its self-loop some number of times. We'll therefore use the following rule:

When eliminating state $q_{gone}$ and adding a transition from $q_{in}$ to $q_{out}\text,$ where $q_{gone}$ has a self-loop, determine the label on the transition as follows:

Let $R_{in}$ be the regex on the transition from $q_{in}$ to $q_{gone}\text.$
Let $R_{stay}$ be the regex on the transition from $q_{gone}$ to itself.
Let $R_{out}$ be the regex on the transition from $q_{gone}$ to $q_{out}\text.$
The resulting regex on the transition from $q_{in}$ to $q_{out}$ is $\left(R_{in}\right)\left(R_{stay}\right)^\star\left(R_{out}\right)\text,$ where the parentheses may be omitted if they don't change the meaning of the resulting regex.

That is, the new regex corresponds to entering $q_1\text,$ looping there as much as we'd like, and then leaving $q_1\text.$ In this case, that ends up being the following regex:

\[\begin{array}{c|c|c} \text{In} & \text{Out} & \text{Regex} \\ \hline q_0 & q_2 & \left(\mathtt{+} \cup \mathtt{a+a}\right)\left(\mathtt{aa}\right)^\star\left(\mathtt{\equiv} \cup \mathtt{a\equiv a}\right) \end{array}\]

We need all the parentheses here so that we have the right operator precedence. It's first choose whether you want $\mathtt{+}$ or $\mathtt{a+a}\text,$ then do some number of copies of $\mathtt{aa}\text,$ and finally choose whether we want $\mathtt{\equiv}$ or $\mathtt{a \equiv a}\text.$

Having computed the regex, let's see what happens when we add that transition in and delete $q_1\text:$

As before, we now have parallel edges to consider, so we'll combine them by making one giant transition with the union of the two input transitions:

As you can see, the regexes are starting to get a lot longer as the number of states drop. That's normal - state elimination often produces very large regular expressions!

Eliminating $q_2$ and $q_0$

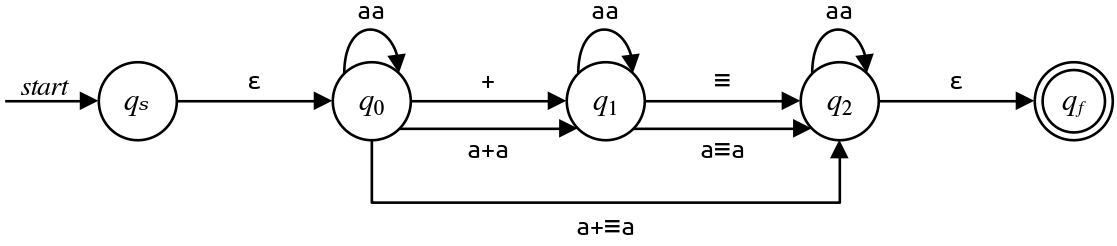
Let's now eliminate $q_2\text.$ We only have one input/output state pair (we have to enter from $q_0$ and end up in $q_f$ after taking the transition). We also see that we have a self-loop on $q_2\text,$ so we'll build the new regex by gluing together the regex on the $q_0$ to $q_2$ transition, the star of the $q_2$ self-loop, and the regex on the $q_2$ to $q_f$ transition. Here's what that looks like:

Now, we could proceed from this point, but we might want to do some brief cleanup first. The transition from $q_0$ to $q_f$ ends with a concatenated $\varepsilon\text,$ which has no effect. Let's simply drop that $\varepsilon$ to keep our very large regex from being a very very large regex. That's shown here:

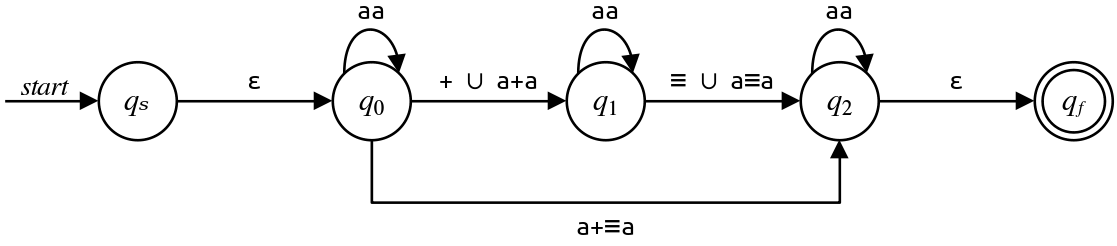
We can now eliminate $q_0\text.$ We'll follow the same procedure as before: glue together the regex on the transition from $q_s$ to $q_0\text,$ then the star of the transition from $q_0$ to itself, and finally the transition from $q_0$ to $q_f\text.$ If we look at what this asks us to do, we can see that we're supposed to glue a $\varepsilon$ on the front of this regex from the $q_s$ to $q_0$ transition, but that has no effect. We'll therefore skip that part and just glue together the self-loop and the transition, giving this final automaton:

We can't eliminate any more states, or we wouldn't have a start state or an accepting state. So we're done with the hard part!

Reading and Interpreting the Regex

The final step of the state elimination algorithm is to read off the overall regex. Here's how that works:

Step Three: The final automaton now just has $q_s$ and $q_f\text.$ The regex is given as follows:

If there is no transition from $q_s$ to $q_f\text,$ the final regex is $\emptyset\text.$
Otherwise, the final regex is the label on the transition from $q_s$ to $q_f\text.$

We are in Case 2 here, so our final regex ends up being

\[\left(\mathtt{aa}\right)^\star\left(\left(\mathtt{+} \cup \mathtt{a+a}\right)\left(\mathtt{aa}\right)^\star\left(\mathtt{\equiv} \cup \mathtt{a \equiv a}\right) \ \cup \ \mathtt{a+\equiv a}\right) \left(\mathtt{aa}\right)^\star\]

This is a very complex regex - how do we know that it's correct? The answer is "we don't unless we test it," the same way that if you solve for $x$ in an equation it's never a bad idea to go back and plug in your final answer to make sure you didn't make any silly math errors. In this case, we've checked the regex, and we're pretty sure it's correct.

Any time you finish doing state elimination, I recommend that you take a few minutes to analyze the regex you got back to see how it works. After all, perhaps the way that it works contains some clever technique or approach that would not have occurred to you earlier. (I've been writing regexes for a long time and am often surprised by what drops out of state elimination!) In this case, how do we interpret the regex?

To make it a bit easier to see what's going on, let's use some color-coding. I'll mark the part of the regex that contributes to the first group of a's in gold, the parts contributing to the second group in teal, and the parts contributing to the final group in purple:

\[\left({\color{olive} \mathtt{aa}} \right)^\star\left(\left(\mathtt{+} \cup \mathtt{ {\color{olive}a}+{\color{teal}a}}\right)\left({\color{teal}\mathtt{aa}}\right)^\star\left(\mathtt{\equiv} \cup \mathtt{ {\color{teal} a} \equiv {\color{purple}a}}\right) \ \cup \ \mathtt{ {\color{olive}{a}}+\equiv {\color{purple} a}}\right) \left( {\color{purple} \mathtt{aa}}\right)^\star\]

It's interesting to see how the groups are built up. All of them are built up two a's at a time. The cases where one group is odd is handled by placing an a on both sides of one of the separator symbols.

When I first read this I was mystified by why there needed to be an $\mathtt{a + \equiv a}$ case. I would definitely recommend taking some time to think this one over - as a hint, how does the regex handle the case where the first and last group have an odd number of a's while the middle group has an even number of a's?

Exercises

Here are some exercises you can use to get more practice with state elimination.

Here is a DFA that acccepts all strings that contain aa as a substring: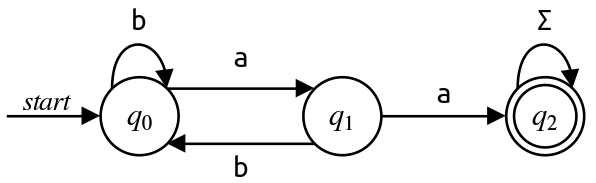

Perform the state-elimination algorithm on this DFA, removing the states in the order $q_2\text,$ $q_1\text,$ $q_0\text.$ What is the resulting regular expression?

Solution

We begin by adding in a new start and accepting state, as shown here:

To eliminate $q_2\text,$ we need to add a transition from $q_1$ to $q_f$ labeled $\mathtt{a}\Sigma^\star\varepsilon\text.$ Concatenating with $\varepsilon$ has no effect here, so we label that transition $\mathtt{a}\Sigma^\star$ instead:

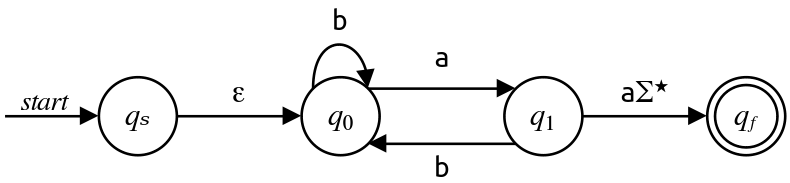
Next, we'll eliminate $q_1\text.$ There are two pairs of in/out states to consider, and the necessary transitions are listed below:
\[\begin{array}{c|c|c} \text{In} & \text{Out} & \text{Regex} \\ \hline q_0 & q_0 & \mathtt{ab} \\ q_0 & q_f & \mathtt{aa}\Sigma^\star \end{array}\]
This is shown here, after collapsing the parallel transitions from $q_0$ to itself:

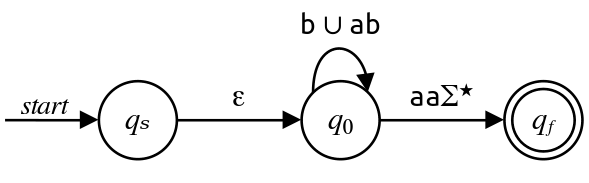
An optional but nice step: we can notice that the regex $\mathtt{b} \cup \mathtt{ab}$ is equivalent to the regex $\mathtt{a}?\mathtt{b}$ and simplify the automaton a bit:

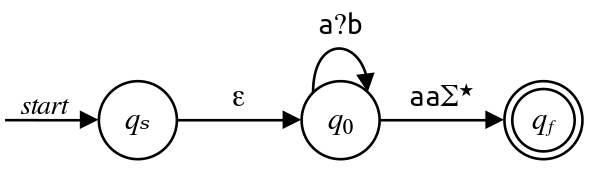
Finally, removing $q_0$ gives us the regex $\varepsilon \left(\mathtt{a}?\mathtt{b}\right)^\star\mathtt{aa}\Sigma^\star\text,$ which we can simplify by dropping the unnecessary concatenated $\varepsilon\text:$

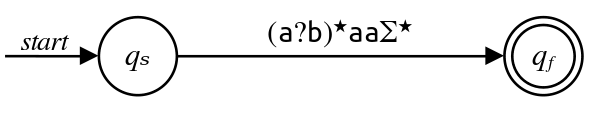
This means that our final regex is $\left(\mathtt{a}?\mathtt{b}\right)^\star\mathtt{aa}\Sigma^\star\text.$ It's worth taking a minute to see why this works.

Perform state elimination on the same automaton as in part (i), but this time using the order $q_0\text,$ then $q_1\text,$ and then $q_2\text.$ What regex do you get back now? This shows that the order in which states are eliminated can influence the form of the final regex. (The resulting regex will always have the same language as the original automaton, though.)

Solution

We begin, as above, by adding in $q_s$ and $q_f\text:$

To eliminate $q_0\text,$ we fill in the following table to determine all the transitions we need to add. I've simplified the table here by removing all unnecessary concatenated $\varepsilon\text{'s:}$
\[\begin{array}{c|c|c} \text{In} & \text{Out} & \text{Regex} \\ \hline q_s & q_1 & \mathtt{b}^\star\mathtt{a} \\ q_1 & q_1 & \mathtt{b}\mathtt{b}^\star\mathtt{a} \end{array}\]
We can further simplify this by noticing that $\mathtt{b}\mathtt{b}^\star$ is more compactly expressed as $\mathtt{b}^+\text.$

Here's what the automaton looks like after removing $q_0\text:$

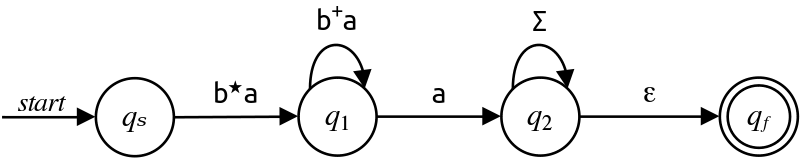
To eliminate $q_1\text,$ we add a transition labeled $\mathtt{b}^\star\mathtt{a}\left(\mathtt{b}^+\mathtt{a}\right)^\star\mathtt{a}$ from $q_s$ to $q_2\text,$ as shown here:

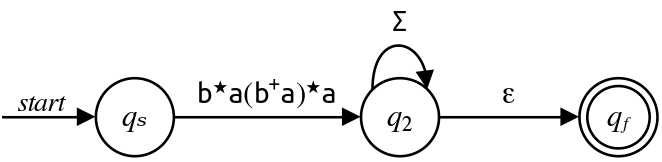
Finally, we eliminate $q_2$ here by adding a transition labeled $\mathtt{b}^\star\mathtt{a}\left(\mathtt{b}^+\mathtt{a}\right)^\star\mathtt{a}\Sigma^\star$ from $q_s$ to $q_f\text.$ (I've already removed the redundant concatenation with $\varepsilon$ here.)

This gives us our final regex, $\mathtt{b}^\star\mathtt{a}\left(\mathtt{b}^+\mathtt{a}\right)^\star\mathtt{a}\Sigma^\star\text.$ It's again worth taking a minute to see why this regex works.

Write a much simple regex for the language of strings that contain aa as a substring than you obtained through either parts (i) or (ii) of these exercises. This shows that while state elimination is guaranteed to always convert a DFA or NFA into a regular expression, the regex you get back might not be the nicest or simplest.

Solution

Here's a very simple regex for this language:
\[\Sigma^\star\mathtt{aa}\Sigma^\star\]
This says "match anything, then aa, then anything."