Guide to CFGs

Context-free grammars are a powerful and flexible tool for specifying languages, but they can take some time to get used to, especially if you’re used to the (much more restricted) world of DFAs, NFAs, and regular expressions. This handout covers three major techniques useful in the design of context-free grammars:

Find a build order. CFGs construct strings in a different order than what you might naturally expect. Once you’re comfortable with this pattern, though, it’s a lot easier to write CFGs.
Think inductively and recursively. Fundamentally, CFGs work by identifying some recursive structure of the strings in a language. Learning to spot these patterns will make it easier for you to write CFGs for more complex languages.
Store information in nonterminals. Using different nonterminals to represent different parts of a string, or different fundamental classes of strings, makes it possible to build CFGs for elaborate structures like spoken and programming languages.

We’ll cover each of these in turn, using some examples to illustrate how each one works.

Find a Build Order

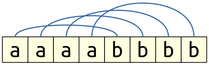
One of the more subtle parts of writing CFGs is figuring out how to build the different pieces of the string up. For example, let’s take this sample CFG for the language $\Set{ \mathtt{a}^n\mathtt{b}^n \suchthat n \in \naturals }$:

\[S \to \mathtt{a}S\mathtt{b} \cfgor \varepsilon\text.\]

Now, let’s pick a string in the language, say, aaaabbbb. Here’s how our grammar derives it:

\[\begin{aligned} S & \Rightarrow \mathtt{a}S\mathtt{b} \\ & \Rightarrow \mathtt{aa}S\mathtt{bb} \\ & \Rightarrow \mathtt{aaa}S\mathtt{bbb} \\ & \Rightarrow \mathtt{aaaa}S\mathtt{bbbb} \\ & \Rightarrow \mathtt{aaaabbbb} \end{aligned}\]

process produces a string of the form $\mathtt{a}^n\mathtt{b}^n$ is that each a is placed down along with one matching b symbol. That means they’re paired off, so the quantities must be the same.

However, the way in which they’re paired off isn’t what you might initially expect when looking at the set $\Set{ \mathtt{a}^n\mathtt{b}^n \suchthat n \in \naturals }$. Intuitively, you might think that they’d pair off this way:

That is, the first a would pair with the first b, the second a with the second b, etc. However, that’s not actually what happens here. Rather, in this CFG, they’re paired off like this:

In other words, they’re matched from the outside in (or inside out, same thing). This is a common pattern in context-free grammars. And in fact, more generally:

☞ CFGs match items from the outside in. ☜

This is important to keep in mind as you’re writing CFGs.

With this in mind, let’s see an example of a CFG. Consider the following language $L$:

$L$ = { $w \in \Set{\mathtt{a}, \mathtt{b}}^\star \suchthat w$’s length is a multiple of three, and the first third of its characters are a’s }

This language happens to be context-free, and our goal will be to write a CFG for it.

A good first thing to do when designing any kind of mathematical model for a language (regular expression, DFA, CFG, etc.) is to write out some example strings to see if we can spot a pattern. In our case, we might start off by writing out some strings like these:

aaaaaa
abb
$\varepsilon$
aaabbb
aababa
aaabbbbbb

It’s also helpful to write out some strings that aren’t in the language:

a
baa
abaaaa
aabbb
aa
aaaabbbb

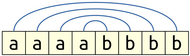
With that in mind, let’s see if we can find a pattern we can use to build up all the strings in the language. The language focuses specifically on the first third of the characters in the string, so perhaps we could think about visually separating those out from the remaining characters, as shown here:

aa|aaaa
a|bb
$\varepsilon$
aa|abbb
aa|baba
aaa|bbbbbb

After splitting things this way, you might notice something – there’s twice as many characters after the line as there are before the line. And that might give us a hint about how to build up these strings. We want to enforce a 1:2 ratio of the characters before the line to the characters after the line. When we had the language $\Set{ \mathtt{a}^n\mathtt{b}^n \suchthat n \in \naturals }$, we enforced a 1:1 ratio between the a’s and the b’s by writing down one b for each a that we wrote. Here, it seems like what we want to do is write down two characters after the line for each one character that we write before the line.

Now we can ask – as we’re writing these characters down, how do we pair them off? From what we discussed earlier in this section, we’ll probably want to build this string from the outside in. This means that might go about pairing the characters like this:

In other words, the first character will pair with the last two characters, and the second character will pair with the two characters before those, etc.

With that in mind, we can take a stab at writing out a CFG for this language. We want something that places down one a at the front of the string and two characters of any type at the back of the string. We can start off with a rough draft, like this:

\[S \to \mathtt{a}S\mathtt{bb} \qquad \text{// still a work in progress}\]

If we look at what these derivations look like, we’ll get patterns like these:

\[\begin{aligned} S & \Rightarrow \mathtt{a}S\mathtt{bb} \\ & \Rightarrow \mathtt{aa}S\mathtt{bbbb} \\ & \Rightarrow \mathtt{aaa}S\mathtt{bbbbbb} \\ & \Rightarrow \mathtt{aaaa}S\mathtt{bbbbbbbb} \\ & \Rightarrow \dots \end{aligned}\]

This is very much on the right track, but there’s a couple of issues. First, we have no way to stop! There’s only one production rule, $S \to \mathtt{a}S\mathtt{bb}$, and if we keep applying that rule we’ll never get rid of the $S$ nonterminal. Second, we’re building a string where the back two-thirds of the string are always b’s, even though we’re supposed to allow for anything there. Let’s address each of these in turn.

First, there’s the issue of terminating this process. At some point, we need to be able to say “okay, we’ve built up everything in the first third, and we’ve build up the last two-thirds, and so I guess we’re done now.” That means we need to get rid of the $S$. And that’s easy to accomplish – we can just add in a production rule that lets us replace $S$ with $\varepsilon$, stopping the construction. That gives us this revised grammar:

\[S \to \mathtt{a}S\mathtt{bb} \cfgor \varepsilon \qquad \text{// still a work in progress}\]

Now, we can build the strings $\varepsilon$, abb, aabbbb, aaabbbbbb, etc., and more generally we have a perfectly correct grammar for the language $\Set{ \mathtt{a}^n\mathtt{b}^{2n} \suchthat n \in \naturals }$. That’s great, but that’s not quite the language we wanted. But it’s still work pausing here to appreciate how we got here!

We now need to fix the other issue, which is that the characters in the back two thirds of the string can be anything, but we’re currently forcing them to all be b’s. What should we do about this?

First, let’s see where this comes from. The production rule $S \to \mathtt{a}S\mathtt{bb}$ is what’s responsible here – this says “put down an a in the front and two b’s in the back.” We’d like to be able to put down whatever we want in the back, not just two b’s.

Second, let’s see how to fix that. In the case of regexes, we have the regex $\Sigma$, which means “any character.” Alas, that’s not how things work with CFGs, and we can’t just write $S \to \mathtt{a}S\Sigma\Sigma$ and call it a day. In CFG Land, $\Sigma$ just means “the character $\Sigma$” and isn’t a catch-all for “any one character.”

Instead, we’ll need to get creative. One option would be to notice that there are only four different combinations of two characters from the alphabet $\Set{\mathtt{a}, \mathtt{b}}$: aa, ab, ba, and bb. We could therefore add in some extra productions to cover all of those possibilities. Here’s what that might look like:

\[S \to \mathtt{a}S\mathtt{aa} \cfgor \mathtt{a}S\mathtt{ab} \cfgor \mathtt{a}S\mathtt{ba} \cfgor \mathtt{a}S\mathtt{bb} \cfgor ε\]

This actually works just fine. For example, here’s how we’d make the string aabaaa:

\[\begin{aligned} S & \Rightarrow \mathtt{a}S\mathtt{aa} \\ & \Rightarrow \mathtt{aa}S\mathtt{baaa} \\ & \Rightarrow \mathtt{aabaaa} \end{aligned}\]

However, I’m not a huge fan of this strategy. For example, suppose that we change our alphabet from the smaller $\Set{\mathtt{a}, \mathtt{b}}$ to the larger $\Set{\mathtt{a}, \mathtt{b}, \mathtt{c}}$. Now there’s nine possible combinations of pairs of characters that can go at the end. If we wanted to adapt this grammar to work in that case, it would look like this:

\[\begin{aligned} S \to & \phantom{\cfgor} \mathtt{a}S\mathtt{aa} \cfgor \mathtt{a}S\mathtt{ab} \cfgor \mathtt{a}S\mathtt{ac} \\ & \cfgor \mathtt{a}S\mathtt{ba} \cfgor \mathtt{a}S\mathtt{bb} \cfgor \mathtt{a}S\mathtt{bc} \\ & \cfgor \mathtt{a}S\mathtt{ca} \cfgor \mathtt{a}S\mathtt{cb} \cfgor \mathtt{a}S\mathtt{cc} \\ & \cfgor \varepsilon \end{aligned}\]

That’s correct, but it’s bulky. And woe unto us if we had the alphabet {a, b, c, d, e, f, $\dots$, z}. I wrote a Python script to generate all the productions that would show up in there thinking it would be fun to include that here, but it filled up so much space that it was just plain obnoxious to skip over. 😃

Fundamentally, the reason this isn’t great is that there’s a mismatch between what we’re trying to say (“any two characters”) and what we’ve done (“anything from this long list, which includes all possible combinations of two characters.”)

To fix this, let’s take a step back. Imagine you were asked to write a CFG just for the language of all length-one strings over the alphabet {a, b, c}. What would that look like? You might put something together like this:

\[T \to \mathtt{a} \cfgor \mathtt{b} \cfgor \mathtt{c}\]

That’s pretty compact, and it’s easy to see how to extend it. If your alphabet gets bigger, you just add more characters here.

Now that we have that, let’s jump back to our original question. How would you say “any two characters” in CFG land? Well, the nonterminal $T$ we built here means “any one character,” so $TT$ would mean “any two characters.” And with that in mind, we can build our final CFG here:

\[\begin{aligned} &S \to \mathtt{a}STT \cfgor \varepsilon \\ &T \to \mathtt{a} \cfgor \mathtt{b} \cfgor \mathtt{c} \end{aligned}\]

Notice that we don’t have that huge explosion of productions from all the possible pairs.

Think Inductively and Recursively

Let’s jump back to our canonical example CFG, the one for $\Set{ \mathtt{a}^n\mathtt{b}^n \suchthat n \in \naturals }$. It’s shown here:

\[S \to \mathtt{a}S\mathtt{b} \cfgor \varepsilon\]

In the preceding section, we traced out a derivation using this grammar to see how it mechanically functions: it places two characters down, one at the front of the string and one at the back of the string, in a way that keeps them nicely paired off. At some point, we say “okay, we’re done” and we stop building the string.

But there’s another way to interpret what these rules say by thinking of them as an inductive construction that builds up every string in the language. We can think of $S \to \varepsilon$ as being a base case: the empty string is in the language $\Set{ \mathtt{a}^n\mathtt{b}^n \suchthat n \in \naturals }$. The production

\[S \to \mathtt{a}S\mathtt{b}\]

can be interpreted as follows. Think of the $S$ in “$\mathtt{a}S\mathtt{b}$” as a placeholder for “some string in the language $\Set{ \mathtt{a}^n\mathtt{b}^n \suchthat n \in \naturals }$.” This rule then says “given a string in the language, you can form another string in the language by taking that string, putting an a on the front, and putting a b on the back.” This would be a way of inductively building up all the strings in the language.

You could also think of this process through a recursive lens. Imagine you have a string $w$ and you want to know whether it’s in this language. Then the production

\[S \to \mathtt{a}S\mathtt{b}\]

could be interpreted in this way. Pretend the $S$ in the middle of $\mathtt{a}S\mathtt{b}$ means “some other string in the language.” Then the rule $S \to \mathtt{a}S\mathtt{b}$ means “to see if your string is in the language, if it starts with a and ends with b, then you can cross off the a and b at the beginning and end and recursively check whether what you have is still in the language.” This process stops once we get to $S \to \varepsilon$, which means “if your string is empty, then it’s in the language.”

This perspective, combined with our insight from earlier about finding a build order, is helpful for designing CFGs. For a more elaborate example of how to put this into practice, let’s take this language:

\[\begin{aligned} L = \{ w \in \Set{\mathtt{a}, \mathtt{b}}^\star \suchthat & w\text{’s length is a multiple of three, and the first third} \\ & \text{of the characters in } w \text{ contains at least one } \mathtt{a} \} \end{aligned}\]

You can think of this language as what you get if you take the language from the previous section and replace a universal quantifier (“every character in the first third is an a”) with an existential quantifier (“at least one character in the first third is an a”). This language happens to be context-free, so let’s take a stab at writing a context-free grammar for it.

But first, as before, let’s write out some sample strings from the language so that we can get a better sense of the lay of the land:

abb
aaabbbbbb
bbabbbbbb
bbbaaaaaaaaa
aaa
aaaaaaaaaaaaaaa
bbbabbbbbbbbbbb
bbabbabba
abbabbabb

As before, it seems like the first third of the string here is significant in some way, so let’s split that section out from what comes afterward:

a|bb
aaa|bbbbbb
bba|bbbbbb
bbba|aaaaaaaa
a|aa
aaaaa|aaaaaaaaaa
bbbab|bbbbbbbbbb
bba|bbabba
abb|abbabb

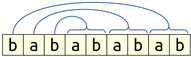
Again, we see the same pattern of “what’s after the line is twice the length of what’s before the line,” and so that might give us the intuition to try pairing off a character before the line with two characters after the line. And we might even guess what order that they’d be paired in; it’s probably going to be something like this:

However, things get a bit trickier than in last time. Last time, we knew, for a fact, that everything before the line was an a and that we could have whatever we wanted after the line. That let us write out a production like $S \to \mathtt{a}STT$, with the idea that the a would go in the front and the two “whatever character we wants” would go to the back. But here, we aren’t guaranteed that what’s in front of the line is an a. We somehow need to ensure that there’s at least one a.

To do this, let’s take a minute to think about this one recursively. Imagine we take a string in the language, like this one here. (I’ve put the separator line in so you can clearly see the first third of the string; as before, that separator line wouldn’t be in the actual string.)

bbabb|aabaaabbab

We have the hunch that we’re going to be peeling off the first character and the last two characters. What happens if we do that here? Well, we’d be left with

babb|aabaaabb

This is a string that’s in our language – its length is a multiple of three, and the first third of the string has at least one a in it. Let’s do that again:

abb|aabaaa

Same deal – it’s still in the language. But watch what happens if we do this again:

bb|aaba

Now we’re left with a string that isn’t in the language. This string has a length that’s a multiple of three, but the first third doesn’t contain an a. What’s going on here? Why did that change this time?

The reason for this has to do with which character we crossed off from the front. The first couple of times we did this, we crossed of a b from the front. When we crossed off a b those times, we knew that what we were left with would still have to have an a somewhere in the front – it just wasn’t the first character. But when we crossed off an a from the front, what we’re left with doesn’t have to have any more a’s at the front. After all, all that’s required is that there is at least one a in the first third of the string, and if we cross off that a we’re not guaranteed that the first third of the string has any more a’s.

This gives us the following pattern:

If you cross a b off from the front of the string and two characters from the back, you’re left with a string whose length is a multiple of three and that must have an a in its first third.
If you cross an a off from the front of the string and two characters from the back, you’re left with a string whose length is a multiple of three, but where there’s no requirements on what the characters in the first third of the string must be.

In other words, what kind of string we’re left with after crossing off the first character (and two from the back) depends on what that first character is. And in fact, we’re left with two different types of strings:

Strings in the language (length is a multiple of three, and the first third contains at least one a).
Strings whose lengths are a multiple of three, with no further requirements.

Since these are two fundamentally different classes of strings, we can imagine building separate CFGs for each of them. Let’s take that second group, for example, which consists of strings whose lengths are a multiple of three with no further restrictions. There are many ways we could write CFGs for that language. Here’s my personal favorite:

\[\begin{aligned} & T \to UUUT \cfgor \varepsilon \\ & U \to \mathtt{a} \cfgor \mathtt{b} \end{aligned}\]

(I’m using the nonterminal $T$ here to denote “a string whose length is a multiple of three,” since we’re ultimately going to reserve the nonterminal $S$ for our overall grammar.) The idea here is that a string whose length is a multiple of three is either

empty, or
will still have a length that’s a multiple of three if you cross off the first three characters.

Take a minute to try out this grammar – isn’t that neat?

Now that we have this nonterminal $T$ written out, we can construct a beautiful CFG for our original language $L$ – strings with a length that’s a multiple of three and whose first third contains at least one a. The idea is to do what we said earlier. We’ll cross off the first character from the string and cross off two characters from the end. But depending on what we cross off from the front, we’ll either (1) recursively be left with a string in the language $L$ or (2) end up with a string whose length is a multiple of three. That’s shown here:

\[\begin{aligned} & S \to \mathtt{b}SUU \cfgor \mathtt{a}TUU \\ & T \to UUUT \cfgor \varepsilon \\ & U \to \mathtt{a} \cfgor \mathtt{b} \end{aligned}\]

Here’s how to interpret this. The nonterminal $S$ represents a string in our language $L$. If you have a string that starts with b and ends with any two characters, apply the rule $S \to \mathtt{b}SUU$ to munch those three characters and be left with some other string in $L$. On the other hand, if your string starts with a and ends with any two characters, then apply the rule $S \to \mathtt{a}TUU$ to munch those characters, then fill in the rest of the string with any collection of characters whose length is a multiple of three.

Store Information in Nonterminals

We arrived at the previous CFG by thinking recursively and finding the right build order – we figured we’d be pairing off the first character of the string with the last two characters, then asked what sort of string would be left after we did so. But there’s another perspective we could take to arrive at that grammar, and, as is always the case, getting multiple perspectives on the same result is helpful in better understanding it.

Look at the production rules just for the nonterminal $S$:

\[S \to \mathtt{b}SUU \cfgor \mathtt{a}TUU\]

One of these production rules is recursive ($S \to \mathtt{b}SUU$ loops back on itself), while the other ($S \to \mathtt{a}TUU$) moves away from $S$ to a different nonterminal $T$. We can therefore think of a derivation starting with $S$ as consisting of “apply the recursive rule $S \mathtt{b}SUU$ until you’re satisfied with the result, then apply the production $S \to \mathtt{a}TUU$ to switch from $S$ to $T$.” For example:

\[\begin{aligned} S & \Rightarrow \mathtt{b}SUU && \text{(“let’s do it again!”)} \\ & \Rightarrow \mathtt{bb}SUUUU && \text{(“yay! more recursion!”)} \\ & \Rightarrow \mathtt{bba}TUUUUUU && \text{(“okay, ready to move on now.”)} \end{aligned}\]

At this point, we’re free to whatever $T$-ish sorts of things we want to do.

This gives us a different view on what $S$ and $T$ mean. We can think of $S$ and $T$ not, as we did before, as standing for classes of strings, but rather as functioning more like the states of a DFA or NFA. When we’re working with $S$, we’re in “phase one” of the construction of the string – laying down some number of b’s at the front and twice as many $U$s at the end. When we’re working with $T$, we’re in “phase two” of building the string – filling in the middle with some string whose length is a multiple of three.

This perspective, using multiple nonterminals to keep track of which “state” of the construction we’re in, is a powerful one that generalizes to a bunch of other languages. For example, let’s take this final example language:

\[\begin{aligned} \{ w \in \Set{\mathtt{a}, \mathtt{b}}^\star \suchthat & w\text{’s length is a multiple of three, and} \\ & \text{the first third of }w\text{ has at least three }\mathtt{a}\text{’s} \} \end{aligned}\]

This language is context free (I mean, it would be a real let-down if it wasn’t, right?), and our task is to figure out how to build a CFG for it.

As usual, let’s start by writing out some sample strings to see if we notice anything. Following the previous convention, I’ll put a separator bar to clearly demarcate what’s in the first third:

aaa|aaaaaa
aaa|bbbbbb
ababa|bababababa
baaa|baaabaaa
abaa|bbbbbbbb
aaab|bbbbbbbb

Now – how would we build a CFG for this language? If you think about it, this language is actually a generalization of what we saw earlier. Specifically, our previous language said that there needed to be at least one a, and here we’re looking for at least three. And how did we build that CFG? As a reminder, it looks like this:

\[\begin{aligned} & S \to \mathtt{b}SUU \cfgor \mathtt{a}TUU \\ & T \to UUUT \cfgor \varepsilon \\ & U \to \mathtt{a} \cfgor \mathtt{b} \end{aligned}\]

In this CFG, the nonterminal $S$ represents “a multiple-of-three string whose first third contains at least one a” and the nonterminal $T$ represents “a multiple-of-three string whose first third contains at least zero a’s.” The production rules for $S$ say either “if you see b up front, you haven’t changed how many a’s there are in the first third,” and “if you see an a up front, you’ve reduced the number of a’s you need to see by one.”

If we interpret $S$ and $T$ to be counting up how many a’s remain to be seen in that first third, then we could think about scaling this up to count up to three a’s by simply adding more nonterminals in the chain. Each nonterminal tracks a quantity of a’s and has productions to either (1) keep that the same or (2) decrease the number of remaining a’s. Here’s one way to make this work.

\[\begin{aligned} & S \to \mathtt{b}SWW \cfgor \mathtt{a}TWW \\ & T \to \mathtt{b}TWW \cfgor \mathtt{a}UWW \\ & U \to \mathtt{b}UWW \cfgor \mathtt{a}VWW \\ & V \to WWWV \cfgor \varepsilon \\ & W \to \mathtt{a} \cfgor \mathtt{b} \end{aligned}\]

Play around with this one – can you tell which nonterminals correspond to which counts?

Some Exercises

To help you play around with these ideas, consider working through these CFG design problems, each of which builds on the ideas from here.

Let $\Sigma = \Set{\mathtt{a}, \mathtt{b}}$ and let $L = \Set{ \mathtt{a}^n\mathtt{b}^m \suchthat m, n \in \naturals \text{ and } n \le m \le 5n }\text.$ Write a CFG for $L$.

Solution

There are many ways you can solve this one. This solution works by repeatedly laying down one a at the front of the string and then at least one and at most five b's at the end of the string:
\[\begin{aligned} & S \to \varepsilon \cfgor \mathtt{a}S\mathtt{b}UUUU \\ & U \to \varepsilon \cfgor \mathtt{b} \end{aligned}\]
Here, the nonterminal $U$ represents "either nothing or a single b."

Let $\Sigma = \Set{\mathtt{a}, \mathtt{b}, \mathtt{c}}$ and let $L = \Set{\mathtt{a}^m\mathtt{b}^n\mathtt{c}^p \suchthat m, n, p \in \naturals \text{ and } m = n\text{ or }m = p }\text.$ Write a CFG for $L$.

Solution

Our approach to this problem works as follows. We'll decide, up top, whether we're looking at the case where $m = n$ or if we're looking at the case where $m = p\text.$

If $m = n\text,$ we are looking at strings of the form $\mathtt{a}^n\mathtt{b}^n\mathtt{c}^p\text,$ where $n$ and $p$ can be chosen however we'd like. We'll thus build up a string of the form $\mathtt{a}^n\mathtt{b}^n$ using our normal strategy, then put down as many c's as we'd like at the end.

If $m = p\text,$ we are looking at strings of the form $\mathtt{a}^n\mathtt{b}^m\mathtt{c}^n\text,$ where $m$ and $n$ can be whatever we'd like them to be. We'll thus start off by laying down a's at the front of the string and c's at the end, then fill in the middle with however many b's we'd like.

Here's what that looks like:
\[\begin{aligned} & S \to X \cfgor Y \\ & X \to RC \\ & R \to \mathtt{a}R\mathtt{b} \cfgor \varepsilon \\ & C \to \mathtt{c}C \cfgor \varepsilon \\ & Y \to \mathtt{a}Y\mathtt{c} \cfgor B \\ & B \to \mathtt{b}B \cfgor \varepsilon \end{aligned}\]
The nonterminal $X$ corresponds to the $m = n$ case and the $Y$ nonterminal to the $m = p$ case. We expand $X$ out to $RC\text,$ where $R$ is strings of the form $\mathtt{a}^n\mathtt{b}^n$ and $C$ is strings of the form $\mathtt{c}^n\text.$

Let $\Sigma = \Set{\mathtt{a}, \mathtt{b}}$ and let $L = \Set{ \mathtt{a}^n\mathtt{b}^m \suchthat m, n \in \naturals \text{ and } m \ne n }\text.$ Write a CFG for $L$.

Solution

These are strings consisting of some number of a's followed by a different number of b's. The key insight here is that if the number of a's and b's aren't the same, then we can regroup the characters of the string into an equal number of a's and b's with either an excess number of a's or an excess number of b's in-between them. Once we have that insight, here's how we'd solve this:
\[\begin{aligned} & S \to \mathtt{a}S\mathtt{b} \cfgor A \cfgor B \\ & A \to \mathtt{a}A \cfgor \mathtt{a} \\ & B \to \mathtt{b}B \cfgor \mathtt{b} \end{aligned}\]
Here, $S$ lays down equal numnbers of a's and b's before filling the gap with a string of one or more a's $(A)$ or one or more b's $(B)\text.$

Let $\Sigma = \Set{\mathtt{a}, \mathtt{b}}$ and let
\[\begin{aligned} L = \{ w \in \Sigma^\star \suchthat & w\text{’s length is a multiple of three and} \\ & \text{the first third of }w\text{ contains an odd number of }\mathtt{a}\text{’s} \}\text. \end{aligned}\]
Write a CFG for $L$.

Solution

This one proceeds along the lines of what we saw in the "store information in nonterminals" section of the Guide. We'll generally proceed by putting one character down at the front of the string and two at the back. As we do, we'll use two different nonterminals to track the parity of the number of a's that we've seen. Each time we put down an a, we'll switch from even parity to odd parity. We'll only allow the string to come to an end when the parity of the number of a's is odd. Here's what that looks like:
\[\begin{aligned} & E \to \mathtt{a}OXX \cfgor \mathtt{b}EXX \\ & O \to \mathtt{a}EXX \cfgor \mathtt{b}OXX \cfgor \varepsilon \\ & X \to \mathtt{a} \cfgor \mathtt{b} \end{aligned}\]
Here, $E$ represents strings with an even number of a's in the first third and $O$ represents strings with an odd number of a's there.