Solving Large Multicommodity Network Flow Problems on GPUs
Manuscript, January 2025.
We consider the all-pairs multicommodity network flow problem on a
network with capacitated edges. The usual treatment keeps track of a
separate flow for each source-destination pair on each edge;
we rely on a more efficient formulation
in which flows with the same destination are aggregated,
reducing the number of variables by a factor equal to the size of the
network. Problems with hundreds of nodes, with
a total number of variables on the order of a million,
can be solved using standard generic interior-point methods on CPUs;
we focus on GPU-compatible algorithms that can solve such problems
much faster, and in addition scale to much larger problems, with
up to a billion variables.
Our method relies on the primal-dual hybrid gradient
algorithm, and exploits several specific features of the problem for
efficient GPU computation.
Numerical experiments show that our
primal-dual multicommodity network flow method accelerates
state of the art generic commercial solvers by
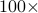to 
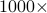, and scales to problems that are much larger.
We provide an open source implementation of our method.