Huffman Coding

CS 106B: Programming Abstractions

Fall 2024, Stanford University Computer Science Department

Lecturers: Cynthia Bailey and Chris Gregg, Head CA: Jonathan Coronado

A diagram showing a huffman-coded tree. Each non-leaf node in the tree has an integer value, and the leaves all hold a letter/frequency combination. The value of a node is the sum of all the frequencies below that node

Slide 2

Announcements

  • Assignment 6 is due tomorrow and Assignment 7 will be out today.

Slide 3

Today's Topics

  • How do we encode ASCII characters?
  • Prefix Codes
  • The Shanon-Fano Algorithm
  • Huffman coding

Note: many of the ideas in this lecture were developed by Eric Roberts, Professor emeritus at Stanford, now at Willamette University (and the author of your CS106B textbook!).

Slide 4

Motivation

  • Today's class is ultimately about Huffman Coding, which is a way to provide lossless compression on a stream of characters or other data. Lossless compression means that we make the amount of data smaller without losing any of the details, and we can decompress the data to exactly the same as it was before compression.
  • This is an absolutely critical part of the digital world that we live in, and virtually everything you do online involves compression. If you open a website on your browser, the web server that delivers the web page to you likely compresses the data, which your browser uncompresses when it receives it. All the images on your screen are compressed. When you transmit video or audio (even on a telephone), the data is compressed when sending and decompressed when receiving.
  • As I said on the first day of class, the video stream you watch when on a Zoom call has a compression of roughly 2000:1, meaning that a 2MB image is compressed down to 1000 bytes! It is incredible that we can do this
    • Incidentally, each individual frame cannot itself be compressed 2000 times, but if you base your encoding scheme on the previous frame, then you can achieve this because most frames are similar to the previous one.
  • Huffman coding is part of most encoding schemes today, so that's why we are studying it.

Slide 5

All characters are just numbers

  • We showed the following ASCII chart in the lecture on strings:

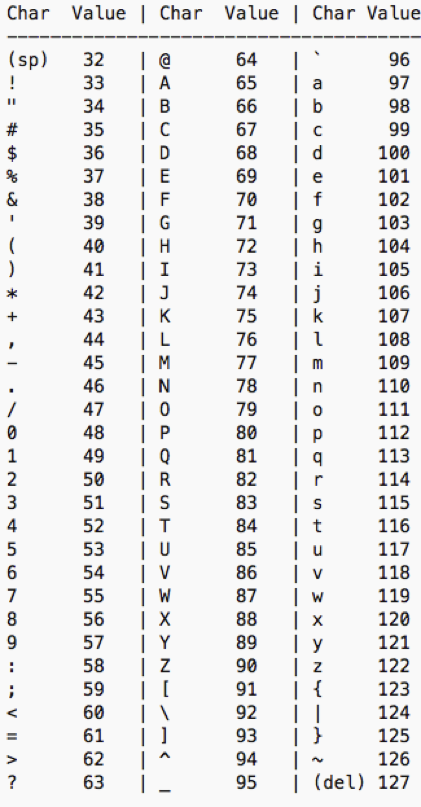
An ASCII table, showing the integer values for the Latin alphabet, numbers, and punctuation

  • Notice that the chart goes from 0 to 127, meaning that there are 128 different values.
    • Why did they stop at 128? Because the original ASCII encoding was for 7-bit numbers, and 2^7 = 128.
    • What is a bit?
      • A bit is a 0 or a 1, and the smallest distinction you can get in mathematics ("off" or "on", "no" or "yes", "false" or "true") – in other words, it is boolean, or binary.
      • When we write numbers in base 2, we only use 0s and 1s.
      • To produce a number in base 2, each digit represents a power of 2 (exactly analogous to how in base 10 each digit represents a power of 10).
      • Here are some examples:
        • Let's look at 23 in base 10: 
          23 = (2 * 10^1) + (3 * 10^0) = 20 + 3
To get the breakdown of the powers of 10, we can do this:
23 / 10 = 2 remainder 3. This means that we start with 3 * 10^0.
Next, we have 2 / 10 = 0 remainder 2, so we have 2 * 10^1
        • We can also look at 23 in base 2: 
          23 / 2 = 11 remainder 1, so we have 1 * 2^0
11 / 2 = 5 remainder 1, so we have 1 * 2^1
5 / 2 = 2 remainder 1, so we have 1 * 2^2
2 / 2 = 1 remainder 0, so we have 0 * 2^3
1 / 2 = 0 remainder 1, so we have 1 * 2^4
  or:
23 = (1 * 2^4) + (0 * 2^3) + (1 * 2^2) + (1 * 2^1) + (1 * 2^0) = 16 + 0 + 4 + 2 + 1
In binary, this is written 10111
  • In order to represent the entire ASCII chart, we need all of the values to have 7 bits, so we pad the front and have 0010111 for 23.
  • These days, we generally use 8 bits (this works better for the memory system we use – you'll learn about that in CS 107!), meaning that all the numbers actually have 8 binary digits.

Slide 6

Can we do better than 8 bits per letter?

  • If we go back to our motivation for a moment: compression is particularly useful when we are sending data across a network.
    • When sending data, we always send one bit at a time (usually as a voltage on a wire, either off or on)
  • With 8 bits per character, we need to send all eight bits for every character.
  • What if we knew something about the data we were sending? For example, what if we knew the frequencies of each letter?
    • In other words, some letters are much more frequent than others (e, t, a -vs- q, k, j), and why can't we change the number of bits so that the most frequent letter takes up the smallest number of bits?
    • You've probably seen this before: Morse Code uses this idea:
      • More frequent English letters have shorter symbols: A Morse Code table. E has a single 'dit' and t has a single 'dash'. A has a dit and a dash. Q has two dashes, a dit, and another dash
  • With a bit stream, if we can create a system that encodes more frequent letters with a shorter number of bits, then we will achieve compression.
  • There is a slight issue, though: if we don't know how many bits we are expecting for a letter, how do we know when to stop collecting bits?
    • We can use what is called a prefix code, in which no character code is the prefix of any other code. So, if we know the codes for all the letters, we will know when to stop, because no two codes share a prefix. We're getting there!

Slide 7

Early Prefix-Coding Strategies

  • In the 1950s, pioneering researchers in information theory developed two strategies for creating a prefix code based on the statistical letter frequencies of English.
  • The Shannon-Fano algorithm invented by Claude Shannon and Robert Fano generates an encoding tree by recursively decomposing the set of possible letters from the top down, finding codes for the most common letters before moving on to codes for the less common ones.
  • The Huffman algorithm developed in 1952 by David Huffman follows much the same strategy but instead builds the encoding tree from the bottom up, combining the least common letter combinations into nodes before working with the higher levels.
  • Huffman coding has considerable advantages and produces a provably minimal encoding for a given pattern of letter frequencies.

Slide 8

The Shannon-Fano Algorithm

  • Even though it is not used in practice, the Shannon-Fano algorithm is useful as a preliminary exercise on the way to developing a better strategy.
  • The pseudocode algorithm for the Shannon-Fano algorithm looks like this:
    1. Arrange the characters in decreasing order of frequency.
    2. Divide the characters close to the frequency midpoint.
    3. Those on the left have a 0 bit; those on the right have a 1.
    4. Apply this algorithm recursively down to single characters.

Slide 9

Illustrating the Shannon-Fano Algorithm

Slide 10

The Huffman Algorithm

  • The Huffman algorithm differs in two important ways from the Shannon-Fano algorithm:
    • It works from the bottom up.
    • It is adaptive, in the sense that the order changes as nodes are combined.
  • The Huffman pseudocode looks like this:
    1. Put all the nodes in a priority queue by frequency.
    2. While there is more than one node in the queue:
      a. Dequeue the first two nodes.
      b. Create a new node with the sum of the frequencies.
      c. Reinsert the new node in the priority queue.

Slide 11

Features of a Huffman tree

  • One interesting feature of Huffman trees is that all nodes will either have two children, or none (the leaves). This is what describes a "well-formed" Huffman tree.
    • (there are two exceptions: an empty Huffman tree would have zero nodes, and a Huffman tree built from data with only a single character–e.g., "AAAAA"–would only have a single node. These are special cases that we don't ask you to build for your implementation).
  • The reason that the trees turn out this way has everything to do with the priority queue and the way they are built. Until there is a single node in the priority queue, you will always dequeue two elements, and they then become the children of another node. It is impossible to build a tree in this fashion without all nodes having either zero or two children.
  • This makes working with Huffman trees slightly easier – assuming they are well-formed, you don't have to worry about checking for single children.

Slide 12

Illustrating Huffman Coding

Slide 13

The Huffman Tree for Scrabble Tiles