1) String Processing (strings.cpp)
Write a function
void reverseInPlace(string& str)
that reverses a string “in-place.” That is, you should take the string to reverse as a reference parameter and modify it so that it ends up holding its reverse. Your function should use only O(1) auxiliary space.
Now, imagine you have a string containing a bunch of words from a sentence. Here’s a nifty little algorithm for reversing the order of the words in the sentence: reverse each individual string in the sentence, then reverse the entire resulting string. (Try it – it works!) Go and code a function
void reverseWordOrderingIn(string& sentence)
that accomplishes this task and uses only O(1) auxiliary storage space.
void reverseInPlace(string& str) {
/* We need to make sure to only loop up to halfway though the string
* or we will end up with the original string! Try it out on
* paper if this isn't clear.
*/
for (int i = 0; i < str.length() / 2; i++) {
char temp = str[i];
str[i] = str[str.length () - 1 - i]; // Question: Why is the -1 here?
str[str.length () - 1 - i] = temp;
}
}
To see that this only uses O(1) storage space, we can account for where all the memory we’re using is coming from. We need space for the integer i and the variable temp, but aside from that there’s no major allocations or storage required.
You can come up with all sorts of different answers to the second problem depending on how you define what a word boundary looks like. We’ve decided to do this by just finding whitespace, but a more intelligent implementation might opt to do more creative checking.
/* Essentially the same function as before, except that we specify our own start
* and end indices so we can reverse parts of a string rather than the whole
* string at each point. The end index is presumed to be one past the end of the
* substring in question.
*/
void reverseInPlace(string& str, int start, int end) {
for (int i = 0; i < (end - start) / 2; i++) {
char temp = str[start + i];
str[start + i] = str[end - 1 - i];
str[end - 1 - i] = temp;
}
}
void reverseWordOrderingIn(string& sentence) {
/* Scan across the sentence looking for words. The start variable holds the
* index of the start point of the current word in the sentence. The variable
* i holds the index of the character we're currently scanning.
*/
int start = 0;
for (int i = 0; i < sentence.length(); i++) {
if (sentence[i] == ' ') {
reverseInPlace(sentence, start, i);
start = i + 1;
}
}
/* We need to account for the fact that there might be a word
* flush up at the end of the sentence.
*/
reverseInPlace(sentence, start, sentence.length());
/* Now reverse everything. */
reverseInPlace(sentence, 0, sentence.length());
}
Again, we can see that we’re using O(1) space because we’re only using a few temporary variables to hold indices and characters.
2) Container Classes (adts.cpp)
Write a function
Map<int, Set<string>> reverseMap(Map<string, int>& map)
that, given a Map<string, int> that associates string values with integers, produces a Map<int, Set<string>> that’s essentially the reverse mapping, associating each integer value with the set of strings that map to it. (This is an old job interview question from 2010.)
Then, consider the following problem. A compound word is a word that can be cut into two smaller strings, each of which is itself a word. The words “keyhole” and “headhunter” are examples of compound words, and less obviously so is the word “question” (“quest” and “ion”). Write a function
void printCompoundWords(Lexicon &dict)
that takes in a Lexicon of all the words in English and then prints out all the compound words in the English language.
Here’s one possible implementation.
Map<int, Set<string>> reverseMap(Map<string, int>& map) {
Map<int, Set<string>> result;
for (string oldKey : map) {
if (!result.containsKey(map[oldKey])) {
result[map[oldKey]] = {};
}
result[map[oldKey]].add(oldKey);
}
return result;
}
bool isCompoundWord(string& word, Lexicon& dict) {
/* Try splitting the word into two possible words for
* every possible position where you can make the split.
*/
for (int i = 1; i < word.length(); i++) {
/* The two words are formed by taking the substring up to the splitting
* point and the substring starting at the splitting point.
*/
if (dict.contains(word.substr(0, i)) && dict.contains(word.substr(i))) {
return true;
}
}
return false;
}
void printCompoundWords(Lexicon &dict) {
for (string word: dict) {
if (isCompoundWord(word, dict)) cout << word << endl;
}
}
3) Big O
Below are eight functions. Determine the big-O runtime of each of those pieces of code.
void function1(int n) {
for (int i = 0; i < n; i++) {
cout << '*' << endl;
}
}
void function2(int n) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cout << '*' << endl;
}
}
}
void function3(int n) {
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
cout << '*' << endl;
}
}
}
void function4(int n) {
for (int i = 1; i <= n; i *= 2) {
cout << '*' << endl;
}
}
void function5(int n) {
if (n == 0) return;
function5(n - 1);
}
void function6(int n) {
if (n == 0) return;
function6(n - 1);
function6(n - 1);
}
void function7(int n) {
if (n == 0) return;
function7(n / 2);
}
void function8(int n) {
if (n == 0) return;
for (int i = 0; i < n; i++) {
cout << '*' << endl;
}
function8(n / 2);
function8(n / 2);
}
Finally, what is the big-O runtime of this function in terms of n, the number of elements in v?
int squigglebah(Vector<int>& v) {
int result = 0;
for (int i = 0; i < v.size(); i++) {
Vector<int> values = v.subList(0, i);
for (int j = 0; j < values.size(); j++) {
result += values[j];
}
}
return result;
}
- The runtime of this code is
O(n): We print out a single star, which takes timeO(1), a total ofntimes. - The runtime of this code is
O(n^2). The inner loop doesO(n)work, and it runsO(n)times for a net total ofO(n^2)work. - This one also does
O(n^2)work. To see this, note that the first iteration of the inner loop runs forn – 1iterations, the next forn – 2iterations, thenn – 3iterations, etc. Adding all this work up across all iterations gives(n – 1) + (n – 2) + … + 3 + 2 + 1 + 0 = O(n^2), as we saw in class when doing the analysis of insertion sort and selection sort. - This one runs in time
O(log n). To see why this is, note that afterkiterations of the inner loop, the value ofiis equal to2^k. The loop stops running when2^kexceedsn. If we set2^k = n, we see that the loop must stop running afterk = log₂ nsteps.
Another intuition for this one: the value of i doubles on each iteration, and you can only doubleO(log n)times before you overtake the valuen. - Each recursive call does a constant amount of work (specifically, it just checks the value of
nand optionally makes a recursive call). The question, then, is how many recursive calls there are. Each recursive call fires off one more recursive call withndecreased by one. AfterO(n)total recursive calls are made, therefore, the value ofnwill drop to zero and we’ll stop. Since we’re doingO(1)workO(n)times, this function takes timeO(n)to run. - As before, each recursive call does O(1) work, and so the question is how many recursive calls are made. This one, however, is more subtle than before. Think about the shape of the recursion tree: each node in the tree will branch and have two nodes beneath it. That means that if we make an initial call of
function6(n), there will be two calls tofunction6(n - 1). Each of those calls fires off two more recursive calls tofunction6(n - 2), so there are four calls tofunction6(n - 2). There’s then eight calls tofunction6(n - 3), sixteen calls tofunction6(n - 4), and more generally2^kcalls tofuncion6(n - k). Overall, the total number of recursive calls made is equal to2^0 + 2^1 + 2^2 + … + 2^nSince these values grow exponentially quickly, the very last one accounts for almost the complete value of the sum, so the work done here isO(1)work per call timesO(2^n)total calls for a total ofO(2^n)work. - Each recursive call here does
O(1)work, as before, so the question is how many calls get made. Notice that the value ofndrops by half each time a recursive call is made, and that can only happenO(log n)times before the value drops all the way to zero. (Remember that integer division in C++ rounds down, so when we get ton = 1the next call will be withn = 0). Therefore, the runtime isO(log n). - Each recursive call here does
O(n)work for the for loop, then makes two recursive calls on two inputs half as big as the original. You might recognize this as the same pattern that mergesort follows! As a result, the runtime here isO(n log n).
For the final function, Let’s follow the useful maxim of "when in doubt, work inside out!"" The innermost for loop (the one counting with j) does work proportional to the size of the values list, and the values list has size equal
to i on each iteration. Therefore, we can simplify this code down to something that looks like this:
int squigglebah(Vector<int>& v) {
int result = 0;
for (int i = 0; i < v.size(); i++) {
Vector<int> values = v.subList(0, i);
do O(i) work;
}
return result;
}
Now, how much work does it take to create the values vector? We’re copying a total of i elements from v, and so the work done will be proportional to i. That gives us this:
int squigglebah(Vector<int>& v) {
int result = 0;
for (int i = 0; i < v.size(); i++) {
do O(i) work;
do O(i) work;
}
return result;
}
Remember that doing O(i) work twice takes time O(i), since big-O ignores constant factors. We’re now left with this:
int squigglebah(Vector<int>& v) {
int result = 0;
for (int i = 0; i < v.size(); i++) {
do O(i) work;
}
return result;
}
This is the same pattern as function2 in the previous problem, and it works out to O(n^2) total time.
4) Recursion (recursion.cpp)
Imagine you have a 2 × n grid that you’d like to cover using 2 × 1 dominoes. The dominoes need to be completely contained within the grid (so they can’t hang over the sides), can’t overlap, and have to be at 90° angles (so you can’t have diagonal or tilted tiles). There’s exactly one way to tile a 2 × 1 grid this way, exactly two ways to tile a 2 × 2 grid this way, and exactly three ways to tile a 2 × 3 grid this way (can you see what they are?) Write a recursive function
int numWaysToTile(int n)
that, given a number n, returns the number of ways you can tile a 2 × n grid with 2 × 1 dominoes.
If you draw out a couple of sample tilings, you might notice that every tiling either starts with a single vertical domino or with two horizontal dominoes. That means that the number of ways to tile a 2 × n (for n ≥ 2) is given by the number of ways to tile a 2 × (n – 1) grid (because any of them can be extended into a 2 × n grid by adding a vertical domino) plus the number of ways to tile a 2 × (n – 2) grid (because any of them can be extended into a 2 × n grid by adding two horizontal dominoes). From there the question is how to compute this. You could do this with regular recursion, like this:
int numWaysToTile(int n) {
/* There's one way to tile a 2 x 0 grid: put down no dominoes. */
if (n == 0) return 1;
/* There's one way to tile a 2 x 1 grid: put down a vertical domino. */
if (n == 1) return 1;
/* Recursive case: Use the above insight. */
return numWaysToTile(n - 1) + numWaysToTile(n - 2);
}
5) Recursive Enumeration and Backtracking (backtracking.cpp)
Given a positive integer n, write a function
void printSumsOf(int n)
that finds all ways of writing n as a sum of nonzero natural numbers. For example, given n = 3, you’d list off these options:
3, 2 + 1, 1 + 2, 1 + 1 + 1
Next, write a function
void listKOrderings(Set<string> choices, int k)
that, given a set of strings and a number k, lists all ways of choosing k elements
from that list, given that order does matter. For example, given the objects A, B, and C and k = 2, you’d list
A B, A C, B A, B C, C A, C B
Finally, we will revisit one of the problems from earlier in this handout. In particular, one of the problems from the "Container Classes" section of this handout discussed compound words, which are words that can be cut into two smaller pieces, each of which is a word. You can generalize this idea further if you allow the word to be chopped into even more pieces. For example, the word "longshoreman" can be split into "long," "shore," and "man," and "whatsoever" can be split into "what," "so," and "ever."" Write a function
void printMultCompoundWords(Lexicon& dict)
that takes in a Lexicon representing the English dictionary and prints out all words in the dictionary that can be split apart into two or more smaller pieces, each of which is itself an English word.
The key insight for the first problem is that some positive number has to come first in our ordering, so we can just try all possible ways of breaking off some initial bit and see what we find.
void printSumsOf(int n) {
/* Handle edge cases. */
if (n < 0) error("Can't make less than nothing from more than nothing.");
printSumsRec(n, {});
}
/* Print all ways to sum up to n, given that we've already broken off the numbers
* given in soFar.
*/
void printSumsRec(int n, Vector<int> soFar) {
/* Base case: Once n is zero, we need no more numbers. */
if (n == 0) {
printAsSum(soFar);
} else {
/* The next number can be anything between 1 and n, inclusive. */
for (int i = 1; i <= n; i++) {
printSumsRec(n - i, soFar + i);
}
}
}
/* Prints a Vector<int> nicely as a sum. */
void printAsSum(Vector<int>& sum) {
/* The empty sum prints as zero. */
if (sum.isEmpty()) {
cout << 0 << endl;
} else {
/* Print out each term, with plus signs interspersed. */
for (int i = 0; i < sum.size(); i++) {
cout << sum[i];
if (i + 1 != sum.size()) cout << " + ";
}
cout << endl;
}
}
The second problem is half combinations, half permutations. We use the permutations strategy of asking "what is the next term in our ordered list?" at each step, and the combinations strategy of cutting off our search as soon as we have enough terms.
void listKOrderings(Set<string> choices, int k) {
/* Quick edge case check: if we want more items than there are options, there
* are no orderings we can use.
*/
if (k < choices.size()) {
listOrderingHelper(choices, k, {});
}
}
void listOrderingHelper(Set<string> choices, int k, Vector<string> soFar) {
/* Base case: If no more terms are needed, print what we have. */
if (k == 0) {
cout << soFar << endl;
}
/* Recursive case: What comes next? Try all options. */
else {
for (string choice: choices) {
listOrderingHelper(choices - choice, k - 1, soFar + choice);
}
}
}
The main insight for the final problem is that a word can be broken apart into two or more words if it can be split into two pieces such that the first piece is a word, and the second piece is either (1) a word or (2) itself something that can be split apart into two or more words.
void printMultCompoundWords(Lexicon& dict) {
for (string word : dict) {
if (isMultCompoundWord(word, dict)) {
cout << word << endl;
}
}
}
bool isMultCompoundWord(string word, Lexicon& dict) {
/* In an unusual twist, our base case is folded into the recursive step. We
* will try all possible splits into two pieces, and if one of them happens
* to be a pair of words, we stop.
*/
/* Try all ways of splitting things. */
for (int i = 1; i < word.length(); i++) {
/* Only split if the first part is a word. */
if (dict.contains(word.substr(0, i))) {
string remaining = word.substr(i);
/* We're done if the remainder is either a word or a compound word. */
if (dict.contains(remaining) || isMultCompoundWord(remaining, dict)) {
return true;
}
}
}
/* Nothing works; give up. */
return false;
}
6) Dynamic Arrays and Classes (BigNum.h/.cpp)
The int type in C++ can only support integers in a limited range (typically, -2^31 to 2^31 – 1). If you want to work with integers that are larger than that, you’ll need to use a type often called a big number type (or “bignum” for short). Those types usually work internally by storing a dynamic array that holds the digits of that number. For example, the number 78979871 might be stored as the array [7, 8, 9, 7, 9, 8, 7, 1] (or, sometimes, in reverse as [1, 7, 8, 9, 7, 9, 8, 7]). Implement a bignum type layered on top of a dynamic array. Your implementation should provide member functions that let you add together two bignums or produce a string representation of a bignum, and a constructor that lets you initialize the bignum to some integer value. For simplicity, you don’t need to worry about negative numbers.
Let’s begin with the interface for our class, which will look like this:
class BigNum {
public:
BigNum(int value = 0); // Default to zero unless specified otherwise.
~BigNum();
std::string toString() const; // Get a string representation
void add(const BigNum& value);
private:
int* digits; // Stored in reverse order
int allocatedSize; // In # of digits
int numDigits; // In # of digits.
void reserve(int space); // Ensure we have space to hold numDigits digits
int numDigitsOf(int value) const; // How many digits are in value?
};
Here, the constructor takes in the value we’ll store. The toString function produces a string representation of the number, and the add function takes in another BigNum and adds its value to the total.
Interally, we’ll represent the BigNum as an array of integers, each of which represents a single digit. The allocatedSize and numDigits variables track how many digits we have space for and how many digits we actually have, respectively. (A note: it’s actually not a good use of space to store each digit as an integer because the int type can hold much, much larger values than a single digit, but for simplicity we’ll opt for that approach. Take CS107 to see some alternatives!)
We’ll also write a function named reserve(), which takes as input a number of digits and then does whatever needs to be done to ensure that we have space for at least that many digits. Think of it as a more cautious version of the grow() function we wrote for our stack type: it’ll make the array bigger, but only if it needs to.
To make the implementation simpler, we’ll store the digits of our number in reverse order, so the number 137 would be stored as 7, 3, 1. This makes the math easier and makes it easier to add digits in, since it’s usually easier to add new items further in an array rather than earlier. The implementation itself is presented below.
BigNum::BigNum(int value) {
/* Set up an initial array of elements. */
digits = new int[kDefaultSize]; // Some reasonable default
allocatedSize = kDefaultSize;
/* Count how many digits are in our number. 0 is an edge case, so we'll make
* this work by reducing the number of digits down to the last one.
*/
numDigits = numDigitsOf(value);
/* Copy the number into the array, one digit at a time. */
for (int i = 0; i < numDigits; i++) {
digits[i] = value % 10;
value /= 10;
}
}
int BigNum::numDigitsOf(int value) const {
/* Pro C++ tip: Since this function doesn't read or write any member
* variables, this should either be a free function or a static member
* function. We didn't discuss those sorts of concerns in CS106B, though.
*/
int result = 1; // All numbers have at least one digit.
/* We've already counted one digit. Now count the rest. */
while (value >= 10) {
result++;
value /= 10;
}
return result;
}
BigNum::~BigNum() {
delete[] digits;
}
string BigNum::toString() const {
/* Because characters are stored in reverse order, we have to scan them
* backwards to make our number.
*/
string result;
for (int i = numDigits - 1; i >= 0; i--) {
result += to_string(digits[i]);
}
return result;
}
void BigNum::add(const BigNum& value) {
/* First, ensure we have space to hold the result. Adding two numbers produces
* a result whose size is at most one digit bigger than either input number.
*/
int digitsToVisit = max(numDigits, value.numDigits);
reserve(1 + digitsToVisit);
/* Use the grade school algorithm to add the numbers. */
int carry = 0;
for (int i = 0; i < digitsToVisit; i++) {
int sum;
if (i < numDigits && i < value.numDigits) sum = digits[i] + value.digits[i] + carry;
else if (i < numDigits) sum = digits[i];
else sum = value.digits[i];
/* Write the one's place. */
digits[i] = sum % 10;
/* Store the carry. */
carry = sum / 10;
}
/* We need at least as many digits as before, plus one if there is a final
* carry.
*/
numDigits = digitsToVisit;
numDigits += (carry != 0) ? 1 : 0;
if (carry == 1) digits[digitsToVisit] = 1;
}
/* Reserving space uses the regular "double in size" trick. */
void BigNum::reserve(int space) {
/* If we have the space, then we don't need to do anything. */
if (space <= allocatedSize) return;
/* Double and copy. We deliberately don't just grow to the size requested,
* since that may not be efficient.
*/
allocatedSize *= 2;
int* newDigits = new int[allocatedSize];
for (int i = 0; i < numDigits; i++) {
newDigits[i] = digits[i];
}
delete[] digits;
digits = newDigits;
}
7) Linked Lists (lists.cpp)
Write a function
ListNode* kthToLast(ListNode* list, int k)
that, given a pointer to a singly-linked list and a number k, returns the kth-to last element of the linked list (or a null pointer if no such element exists). How efficient is your solution, from a big-O perspective? As a challenge, see if you can solve this in O(n) time with only O(1) auxiliary storage space.
There are a couple of ways we could do this. One option would be to sweep across the list from the front to the back, counting how many nodes there are, then calculate the index we need. That’s shown here:
int listLength(ListNode* list) {
int count = 0;
/* Cute little for loop trick to visit everything in a linked list. This loop
* is great if you are not making any changes to the list, but if the list is
* either being rewired or being deallocated, this loop won't work.
*/
for (ListNode* curr = list; curr != nullptr; curr = curr->next) {
count++;
}
return count;
}
ListNode* kthToLastSimple(ListNode* list, int k) {
/* Find length of the list */
int len = listLength(list);
/* If the list is too small, just return nullptr. */
if (len < k) return nullptr;
/* Move len - k + 1 steps into the list */
ListNode* curr = list;
for (int i = 0; i < len - k; i++) {
curr = curr->next;
}
return curr;
}
Another option, which is a bit less obvious but is quite beautiful, is to walk down the list with two concurrent pointers, one of which is k steps ahead of the other. As soon as the lead pointer falls off the list, the pointer behind it is k steps from the end. Do you see why?
ListNode* kthToLast(ListNode* list, int k) {
/* Set up two pointers, one leader and one follower. */
ListNode* leader = list;
ListNode* follower = list;
/* March the leader k steps forward. If we fall of the list in this time,
* there is no kth-to-last node.
*/
if (leader == nullptr) return nullptr;
for (int i = 0; i < k; i++) {
/* Question to ponder: Why are there two checks, above and here? */
if (leader == nullptr) return nullptr;
leader = leader->next;
}
/* Keep walking the leader and follower forward. As soon as the leader walks
* off the follower is in the right spot.
*/
while (true) {
if (leader == nullptr) return follower;
leader = leader->next;
follower = follower->next;
}
}
8) Sorting (sorting.cpp)
Write an implementation of insertion sort that works on singly-linked lists. Implement the following function header:
void listInsertionSort(ListNode*& list)
The singly-linked list requirement here suggests that our pattern of repeatedly swapping elements back in the sequence is not going to be easy to implement – we’ll keep losing track of where our preceding element is. There are many ways we could deal with this. One would be to build the sorted list in reverse, then fix up the pointers at the end to reverse it. Another, shown below, works by taking the element, moving it to the front of the list, then swapping it forward until it’s in the right position.
void listInsertionSort(ListNode*& list) { // Question to ponder: why by reference?
ListNode* sortedList = nullptr;
ListNode* curr = list;
while (curr != nullptr) {
/* Need to store the pointer to the next cell in the list, since after
* we do the insert operation we'll lose track of where the next cell
* is.
*/
ListNode* next = curr->next;
sortedInsert(curr, sortedList);
curr = next;
}
list = sortedList;
}
/* Adds the given node into a sorted, singly-linked list. */
void sortedInsert(ListNode* toIns, ListNode*& list) {
/* See if we go at the beginning. */
if (list == nullptr || toIns->value < list->value) {
toIns->next = list;
list = toIns;
} else {
/* Find the spot right before where we go, since that's the pointer we
* need to rewire.
*/
ListNode* curr = list;
ListNode* prev = nullptr;
while (curr != nullptr && curr->value < toIns->value) {
prev = curr;
curr = curr->next;
}
/* Splice us in. */
toIns->next = curr;
prev->next = toIns;
}
}
9) Trees (trees.cpp)
A binary tree (not necessarily a binary search tree) is called a palindromic tree if it’s its own mirror image. For example, the tree on the left is a palindromic tree, but the tree on the right is not:
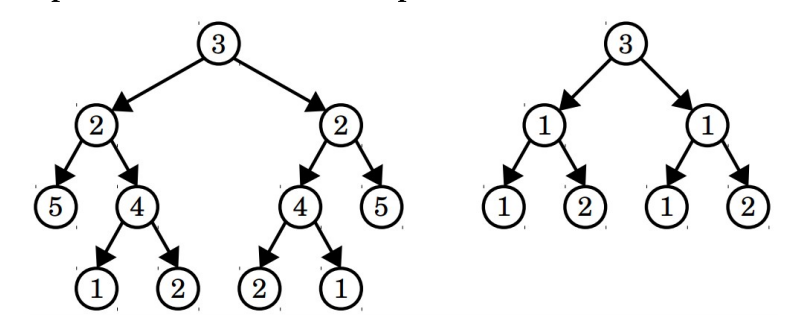
Write a function
bool isPalindromicTree(TreeNode* root)
that takes in a pointer to the root of a binary tree and returns whether it’s a palindrome tree.
To solve this problem, we’ll solve a slightly more general problem: given two trees, are they mirrors of one another? We can then check if a tree is a palindrome by seeing whether that tree is a mirror of itself.
bool isPalindromicTree(TreeNode* root) {
return areMirrors(root, root);
}
bool areMirrors(TreeNode* root1, TreeNode* root2) {
/* If either tree is empty, both must be. */
if (root1 == nullptr || root2 == nullptr) {
return root1 == root2;
}
/* Neither tree is empty. The roots must have equal values. */
if (root1->data != root2->data) {
return false;
}
/* To see if they're mirrors, we need to check whether the left subtree of
* the first tree mirrors the right subtree of the second tree and vice-versa.
*/
return areMirrors(root1->left, root2->right) &&
areMirrors(root1->right, root2->left);
}