Exam instructions: There are 6 questions. Write all answers directly on the exam. This printed exam is closed-book and closed-device; you may refer only to your one letter-sized page of prepared notes and the provided reference sheet. You have 3 hours to complete the exam.
C++ coding guidelines: Unless otherwise restricted in the instructions for a specific problem, you are free to use any of the CS106 libraries and classes we've covered in class. You don't need #include statements in your solutions, just assume the required vector, strlib, etc. header files are visible. You do not need to declare prototypes. You are free to create helper functions unless the problem states otherwise. Comments are not required, but when your code is incorrect, comments could clarify your intentions and help earn partial credit.
Q1) Unique Grid Distance Puzzle (15 points)
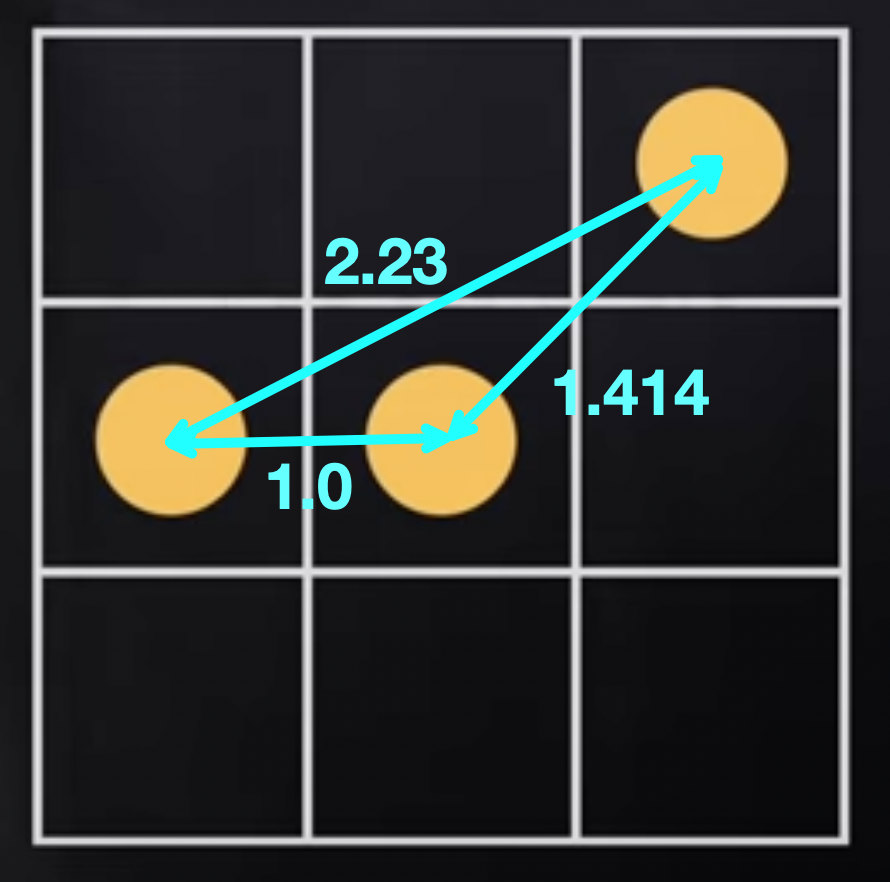
Consider a puzzle that places n circles on an n x n grid, with the intent to have distinct distances between the center of all of the circles. For example, here is a 3 x 3 grid with three circles:

The above circle placement is a solution to the puzzle because the circle centers are placed such that no two circles are the same distance apart:
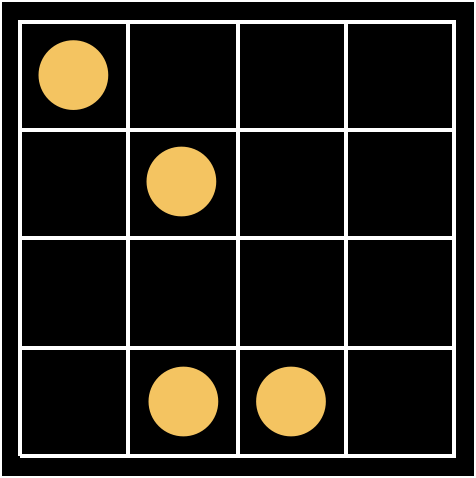
Here is another solution for four circles on a 4 x 4 grid:
However, the following grid is not a solution, because the circle located at row=0, col=1 is the same distance to both of the other circles:

For this problem, you are to write two functions. The first function, isUniqueSolution determines if a vector of GridLocations consists of circles that are uniquely distanced from each other. You can assume you have a function called euclidianDistance that returns the distance between two GridLocations (as a double):
bool isUniqueSolution(Vector<GridLocation> circles)
The second function is a recursive helper function, findUniqueDistancesHelper which populates a Set<Vector<GridLocation>> with all possible solutions for an n x n grid with n circles. A solution is a vector of n GridLocations that will return true when passed into isUniqueSolution().
void findUniqueDistancesHelper(const int n, Vector<GridLocation> &circles, Set<Vector<GridLocation>> &solutions, int row, int col)
The helper function will be called as follows:
Set<Vector<GridLocation>> findUniqueDistances(int n) {
// n is the number of circles we need to place
// on a grid of n x n locations
Vector<GridLocation> circles;
Set<Vector<GridLocation>> solutions;
findUniqueDistancesHelper(n, circles, solutions, 0, 0);
return solutions;
}
Notes:
- You do not need to use any
Gridsfor this solution. - Recall that a
GridLocationhas arowandcolfield, and you can create aGridLocationas follows:GridLocation loc = {1, 2}; // a location at row 1, col 2. - All of the solutions in the set should have
nGridLocations. - Circles cannot go on top of each other. In other words, solutions will always have
ndistinct circles on the grid in different locations.
Your code here:
bool isUniqueSolution(Vector<GridLocation> circles) {
}
void findUniqueDistancesHelper(const int n, Vector<GridLocation> &circles, Set<Vector<GridLocation>> &solutions, int row, int col) {
}
Q2) Classes and Dynamic Memory (15 Points)
Your task is to write a Section class. This class will store information on a single discussion section in CS106B. You can assume you have access to the following Student struct:
struct Student {
string name;
int suid;
/*
* This Vector contains the section preferences
* of a student as string. You can assume that
* there are >= 0 elements in this Vector.
* The Vector is formatted such that index 0
* holds the student's top preference, index
* 1 holds the students 2nd preference, etc.
*/
Vector<string> preferences;
};
Here's the interface for Section, which stores all the students enrolled in that section as a dynamically-allocated array of Students.
// Section.h file
class Section {
public:
/*
* Constructor
* ------------
* The constructor takes in a maximum capacity, and a
* meeting time.
* You can assume the capacity of the section will
* never change.
*/
Section(int capacity, string time);
/*
* Destructor
* ----------
* Cleans up any memory associated with the object.
*/
~Section();
/*
* Method: tryAddStudent
* ---------------------
* Takes in a student and returns true/false based on
* whether or not the student can be enrolled in this
* section. A student can be enrolled in the section if:
*
* - The section time is in the student's
* top 3 preferences
* - The section is not full
*
* Notes:
* - Students should be added to the internal array in
* ascending order of preference.
*
* - You can assume one student won't try to enroll twice
* in the same section.
*
* - This method must run in a worst-case Big-O of O(n)
* where n is the number of elements in the internal array
*
* - You can assume that all section time strings given to
* the class methods are formatted the same way (i.e. the
* time given to the constructor is formatted the same way
* as the times in the student's preferences)
*/
bool tryAddStudent(Student s);
/*
* Method: getStudent
* ------------------
* Takes in an index and returns the student at that
* index. Throws an error if the index is invalid.
*/
Student getStudent(int index);
/*
* Provided Method: swap
* ---------------------
* Takes in two indices and swaps the Students at those
* two indices in the internal array. You can assume
* this function is implemented and fully functional.
*
* YOU DO NOT NEED TO IMPLEMENT THIS FUNCTION
*/
void swap(int index1, int index2);
private:
/* TODO */
};
- Write the
privatesection of the header file - Write the full class implementation (i.e. what would go in the
Section.cppfile)
Note: you can assume that all section time strings given to the class methods are formatted the same way.
Your code here:
// Section.h
class Section {
public:
// ... see above
private:
};
// Section.cpp
#include "Section.h"
Section::Section(int capacity, string time) {
}
Section::~Section() {
}
bool Section::tryAddStudent(Student s) {
}
Student Section::getStudent(int index) {
}
Q3) Linked Lists (15 Points)
Your task is to write a function called listDivisibleBy that takes in a linked list and returns a linked list comprised only of values in the input that are divisible by a certain number.
Say we have a linked list as follows:
4 -> 7 -> 20 -> 8 -> 5 -> 0
called front. Calling listDivisibleBy(front, 4) would return the following list:
4 -> 20 -> 8 -> 0
and front would be edited to be:
7 -> 5
Here's the full function signature you'll be writing:
ListNode* listDivisibleBy(ListNode*& front, int divisor)
Some notes on this problem:
- Your solution should not allocate any new
ListNodes. As such, you shouldn't usenewanywhere in your solution. - The nodes in the returned list should be in the same order they were in in the original list, and the nodes remaining in the original list should also be in the same order they were originally in.
- Be aware that if the first value in the original list is divisible by the number,
frontwill be a different pointer when the function closes (and also note thatfronthas been passed into the function by reference). - You can assume the
divisorparameter won't be 0 - 0 is divisible by all numbers. The only exception is that 0 is not divisible by 0, but this doesn't matter here since
divisorwill never be 0 - If all numbers in the input list are divisible by the
divisor,frontshould benullptrat the end of the function - Here is the
ListNodestruct, for reference:
struct ListNode {
int data; /* Data stored in the node. */
ListNode* next; /* Pointer to next node in the list. */
// default constructor, does not initialize
ListNode() {}
// two-arg constructor
ListNode(int d, ListNode* n) {
data = d;
next = n;
}
};
Your code here:
ListNode* listDivisibleBy(ListNode*& front, int divisor) {
}
Q4) Trees (20 Points)
There are 3 parts to this problem. All three parts are based on the following TreeNode definition:
struct TreeNode {
int data;
TreeNode *left;
TreeNode *right;
// default constructor does not initialize
TreeNode() {}
// 3-arg constructor sets fields from arguments
TreeNode(int d, TreeNode* l, TreeNode* r) {
data = d;
left = l;
right = r;
}
};
A tree is defined by its root. There are no pre-defined tree functions (e.g., you do not have findMin() or add(), etc.).
Part A: Difference of Max and Min in a BST
For this problem, write a function that returns the difference of the maximum and minimum values in a Binary Search Tree (BST). Your function must be O(log n) for full credit:
int diffMaxMinBst(TreeNode *root)
Notes:
- This function should not be recursive, and it cannot have any helper functions.
- As an example, if the maximum value in the tree is 42, and the minimum value is 11, then the function should return 31.
- Negative values in the tree are allowed.
- Remember that Big O disregards constants, so O(2 log n) is equivalent to O(log n).
Your code here:
int diffMaxMinBst(TreeNode *root) {
}
Part B: Difference of Max and Min in a non-BST
For this problem, write a function that returns the difference of the maximum and minimum values in a non-Binary Search Tree. You cannot assume any orderings of the nodes in the tree. Your function must be O(n) for full credit:
int diffMaxMinNonBst(TreeNode *root)
Notes:
- You are welcome to write one or more helper functions for this problem.
Your code here:
int diffMaxMinNonBst(TreeNode *root) {
}
Part C: Create a complete, balanced BST from a sorted vector
For this problem, write a function that creates a complete, balanced Binary Search Tree (BST) from a sorted vector. Recall that a complete tree is a tree that has all of its levels filled from left-to-right except for (possibly) the last level.
TreeNode *balancedBstFromSortedVec(Vector sortedVec)
Notes:
- The solution does not require any helper functions, though you are welcome to write one or more helper functions for this problem if you wish.
Your code here:
TreeNode *balancedBstFromSortedVec(Vector sortedVec) {
}
Q5) Hashing (9 Points)
There are two questions to answer for this problem.
Question A: Hashing – multiple choice, choose all answers that are correct
A good hash function suitable for a hash table should:
- A. Be deterministic
- B. Be reversible (you take a hash code and derive what input produced it)
- C. Create an even distribution across buckets
Question B: Hashing – multiple choice, choose the best answer
What does it mean for a hash table to use chaining?
- A. Each hash bucket holds a linked list for elements that collide when hashed.
- B. The next hash is based on the previous valued added to the hash table, so collisions are avoided.
- C. All values in the table are linked together with hash nodes, avoiding collisions.
- D. The hash function for each bucket depends on the function for the previous bucket, limiting collisions.
- E. The hash values form a increasing or decreasing sequence based on the hash table direction, meaning that collisions can be differentiated from each other.
Q6) BFS, Dijkstra's Algorithm, and A* Algorithm (9 points)
There are three questions to answer for this problem. They are all are based on the following graph:
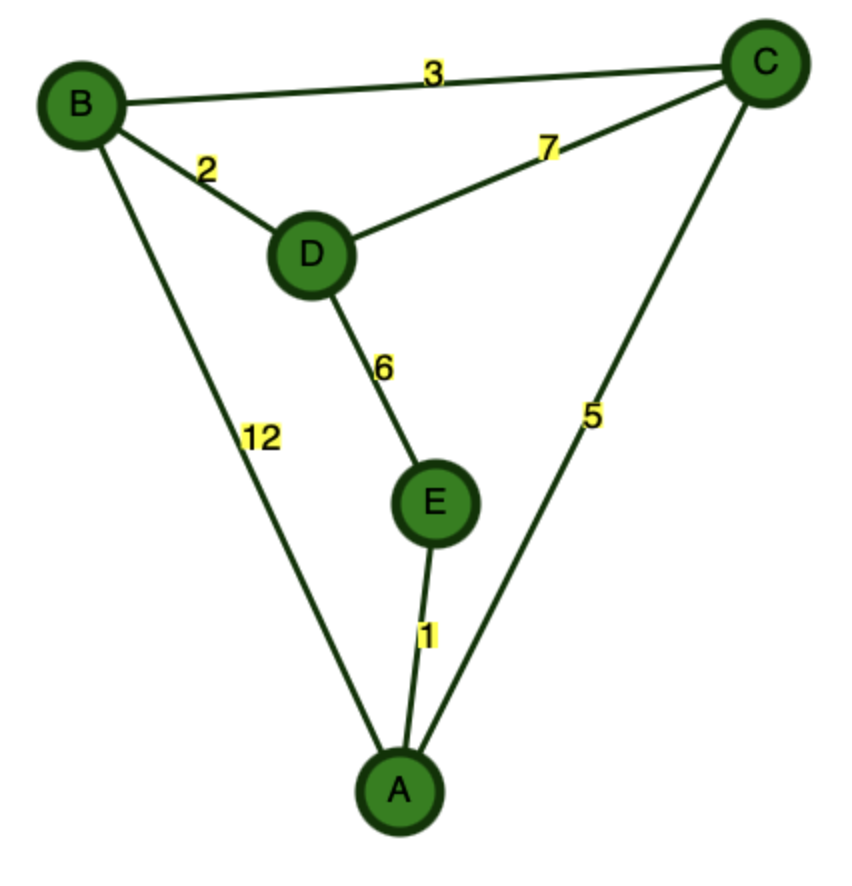
Question A: Breadth First Search – multiple choice, choose the best answer.
If a breadth first search (BFS) was run to determine the shortest path from node A to node B in the graph, what would the algorithm return?
- A. A->B
- B. A->E->D->B
- C. A->C->B
- D. A->C->D->B
Question B: Dijkstra's Algorithm – multiple choice, choose the best answer.
If Dijkstra's Algorothm was run to determine the shortest path from node A to node B in the graph, what would the algorithm return?
- A. A->B
- B. A->E->D->B
- C. A->C->B
- D. A->C->D->B
Question C: A* Algorithm – multiple choice, choose the best answer.
If an A* Algorithm was run to determine the shortest path from node A to node B in the graph, what would the algorithm return?
- A. A->B
- B. A->E->D->B
- C. A->C->B
- D. A->C->D->B