Exam instructions: There are 6 questions. Write all answers directly on the exam. This printed exam is closed-book and closed-device; you may refer only to your one letter-sized page of prepared notes and the provided reference sheet. You have 3 hours to complete the exam.
C++ coding guidelines: Unless otherwise restricted in the instructions for a specific problem, you are free to use any of the CS106 libraries and classes we've covered in class. You don't need #include statements in your solutions, just assume the required vector, strlib, etc. header files are visible. You do not need to declare prototypes. You are free to create helper functions unless the problem states otherwise. Comments are not required, but when your code is incorrect, comments could clarify your intentions and help earn partial credit.
Q1) Linked Lists (15 points)
Write a function
ListNode *mergeListsAndReverse(ListNode *listA, ListNode *listB);
that merges two sorted linked lists and also reverses the output, and returns a pointer to the head of the merged and reversed list. The function should not create or delete any ListNodes. Instead, it should rewire the nodes to form one complete linked list which is sorted in reverse order.
The ListNode struct is defined as follows:
struct ListNode {
int data;
ListNode *next;
};
For example, listA and listB below should be merged into a single reversed linked list, and the pointer to the new head should be returned.
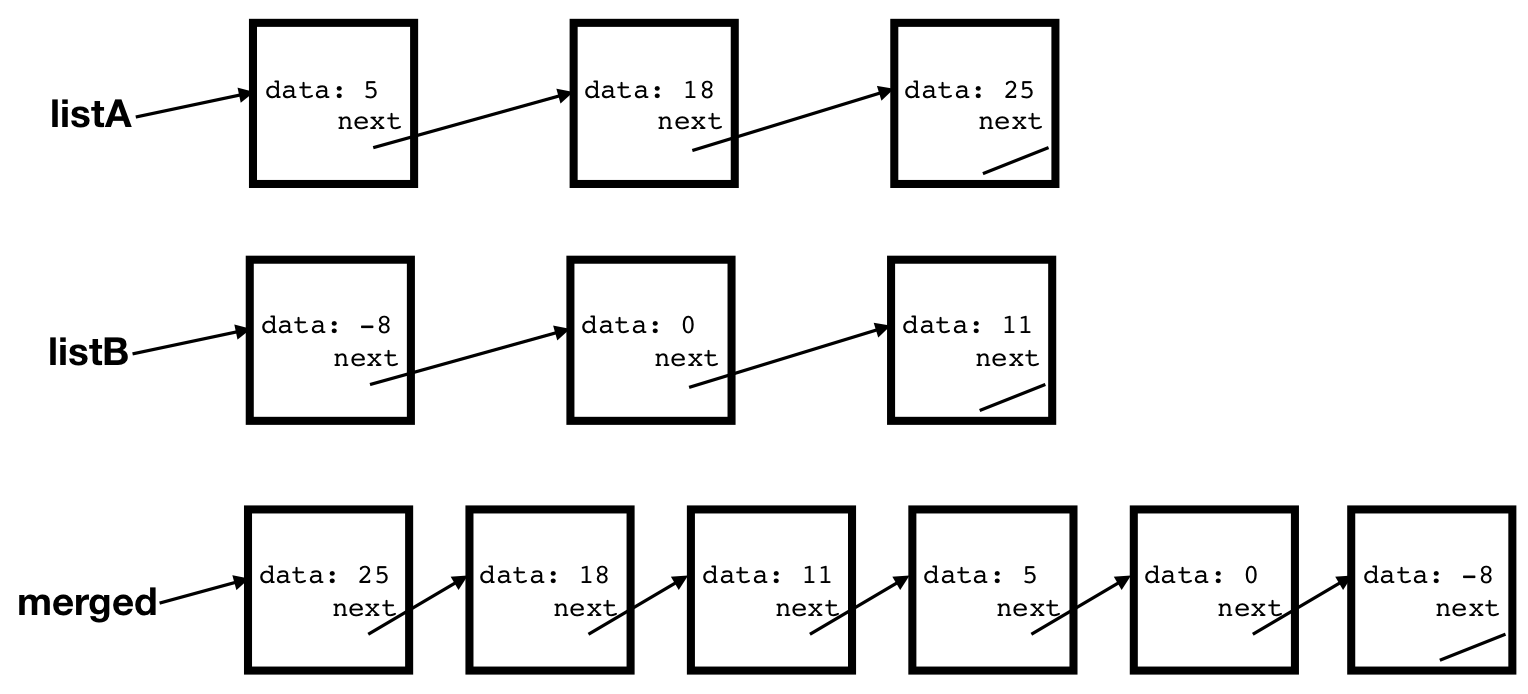
Notes:
- Either or both of the original lists can be empty.
- Your solution should travese the lists only once. A correct solution that traverses the list more than once will lose 50% of the points for this problem.
- You are not allowed to create any additional data structures (e.g.,
Vector, etc.) for your solution. - You should not create any
ListNodeobjects, although you are allowed to create as manyListNode *pointers as you need. - You are not allowed to change any of the
datafields of theListNodeobjects.
Your code here:
ListNode *mergeListsAndReverse(ListNode *listA, ListNode *listB) {
}
Q2) Binary Search Trees (25 Points)
For this problem, you will be writing a simplified Binary Search Tree class, BST that has the following header file:
// bst.h
#pragma once
struct BST_Node {
int data;
BST_Node *left;
BST_Node *right;
};
class BST {
public:
BST(); // constructor
~BST(); // destructor
// insert value into BST, ignoring duplicates
void insert(int value);
// removes all nodes less than min and greater than max
void removeOutOfRangeNodes(int min, int max);
// prints the in-order representation of the tree
// in the following form:
// 1,2,3,4
// with an endl after the list of values.
void printTreeInOrder();
private:
BST_Node *root;
// helper function for insert
void insert(BST_Node *&n, int value);
// cleans up the BST
void deleteTree(BST_Node *n);
// add more private functions if needed
};
Complete the code for each function, and add private helper functions as necessary.
The following program is an example of how the class is used:
1 #include <iostream>
2 #include "bst.h"
3 using namespace std;
4
5 int main() {
6 Vector<int> values = {8,5,11,2,7,9,12,6,10,13};
7 BST tree;
8
9 for (int v : values) {
10 tree.insert(v);
11 }
12
13 tree.printTreeInOrder();
14 tree.removeOutOfRangeNodes(3,9);
15 tree.printInOrder();
16 return 0;
17 }
The output from the program is:
2,5,6,7,8,9,10,11,12,13
5,6,7,8,9
The tree formed by the for loop should look like this:
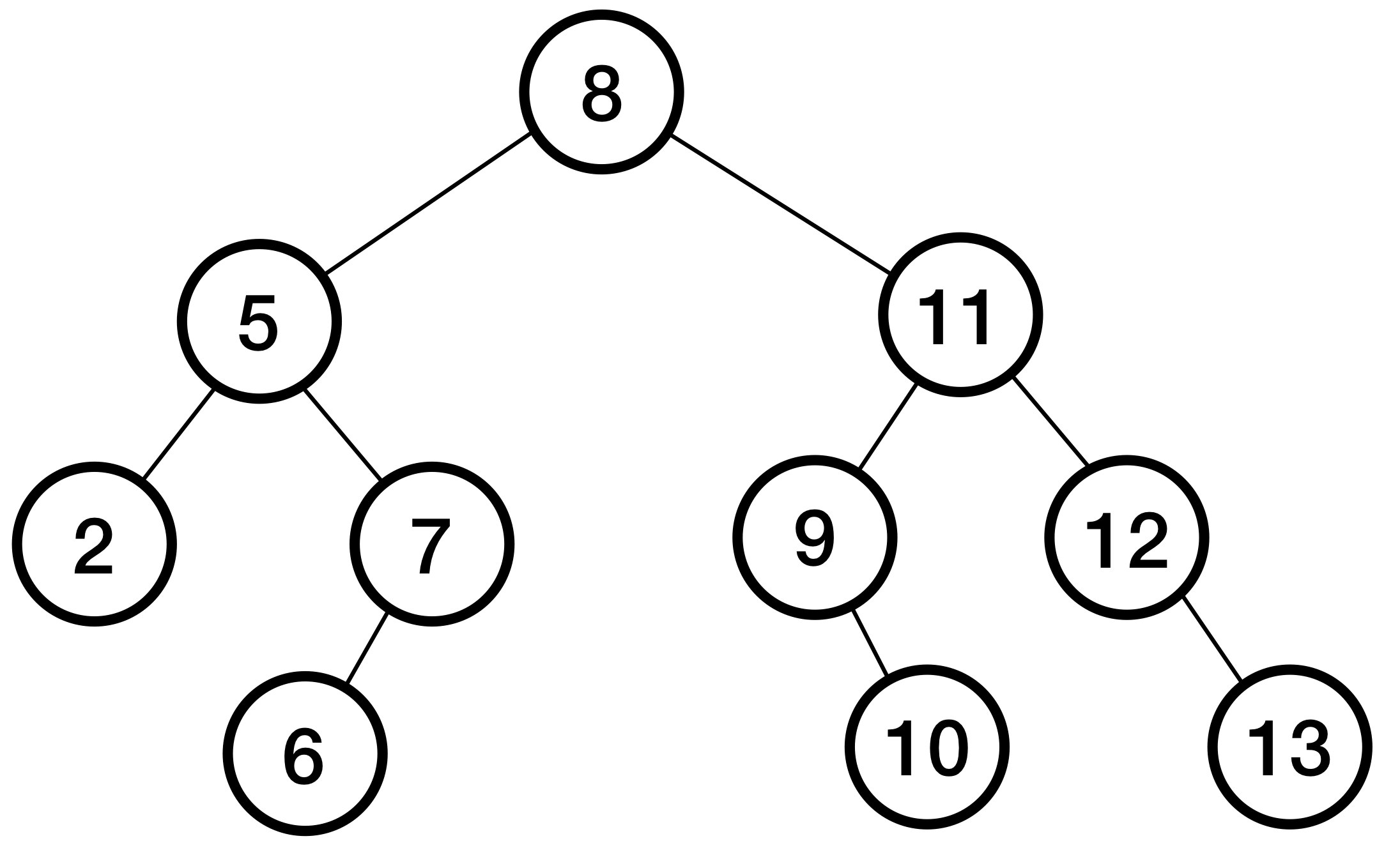
The tree after removing the nodes should look like this:
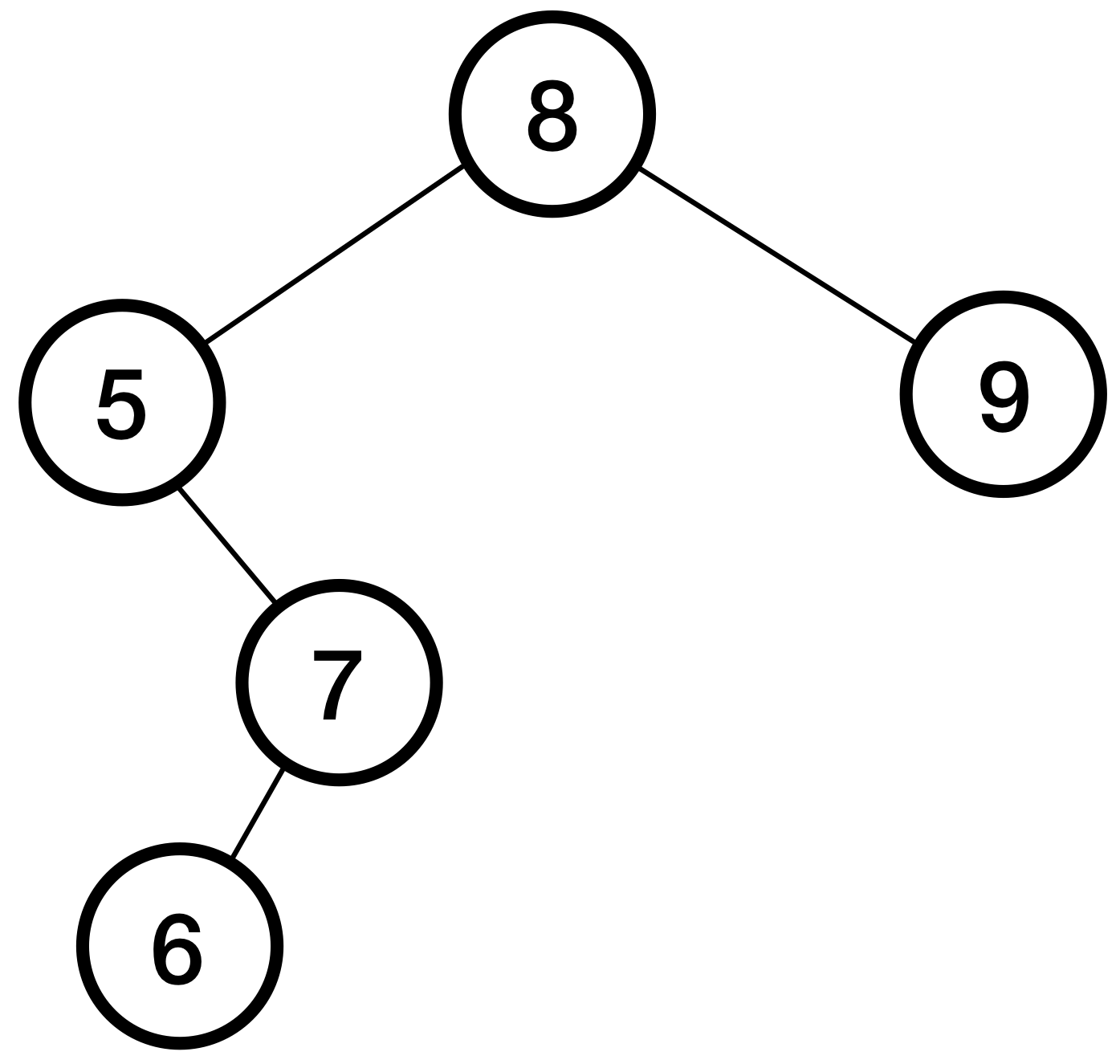
Notes:
- The
BSTclass is not a balanced tree. - The destructor should clean up all nodes in the tree.
- The private
insertfunction should create a newBST_Nodeas necessary. If a value is already represented in the tree,insertshould not duplicate it. - The
removeOutOfRangeNodesfunction removes all nodes less thanminand greater thanmax. You should think this function through carefully - it does not require multiple special-case removal strategies. - The
removeOutOfRangeNodesfunction should not leak memory. If it removes a node, it should calldeleteon that node. - If all nodes are removed from the tree, the
rootof the tree should benullptr. - You are not allowed to add new instance variables to the class.
Your code here:
BST::BST() {
}
BST::~BST() {
}
void BST::insert(int value) {
}
void BST::removeOutOfRangeNodes(int min, int max) {
}
void BST::printTreeInOrder() {
}
void BST::insert(BST_Node *&n, int value) {
}
void deleteTree(BST_Node *n) {
}
Q3) Recursion - Wildcard Matches (15 Points)
Most operating systems and many applications that allow users to work with files support wildcard patterns, in which special characters are used to create filename patterns that can match many different files. The most common special characters used in wildcard matching are ?, which matches any single character, and *, which matches any sequence of characters. Other characters in a filename pattern must match the same character in a filename. For example, the pattern *.* matches any filename that contains a period, such as US.txt or pathfinder.cpp, but would not match filenames that do not contain a period. Similarly, the pattern test.? matches any filename that consists of the name test, a period, and a single character; thus, test.? matches test.h or test.c, but not test.cpp. These patterns can be combined in any way you like. For example, the pattern ??* matches any filename containing at least two characters.
Write a function:
bool filenameMatches(string filename, string pattern);
that takes two strings, representing a filename and a wildcard pattern, and returns true if that filename matches the pattern. Thus,
filenameMatches("US.txt", "*.*")returnstruefilenameMatches("test", "*.*")returnsfalsefilenameMatches("test.h", "test.?")returnstruefilenameMatches("test.cpp", "test.?")returnsfalsefilenameMatches("x", "??*")returnsfalsefilenameMatches("yy", "??*")returnstruefilenameMatches("zzz", "??*")returnstrue
This problem is easier than it might seem at first, if you choose the right recursive decomposition. To help lead you in that direction, start by thinking about the first character in the pattern and distinguish the following cases:
- The pattern string is empty and therefore has no first character.
- The first character in the pattern string is a
?. - The first character in the pattern string is a
*. - The first character in the pattern string is any other character.
In each of these cases, think about what the filename string would have to look like in order to be a match. As in any recursive formulation, the strategy you choose has to reduce complex problems into simpler instances of the same problem.
In writing your answer to this problem, you should keep the following ideas in mind:
- The period (
.) that typically separates parts of a filename is not a special character as far asfilenameMatchesis concerned. A period in pattern means that there must be a period in filename, which is exactly what happens with any other character. - The
*character can match any substring in filename, including an empty substring of length 0. - If you find yourself getting bogged down in lots of detailed code, you are probably veering off onto the wrong track. Go back and look at the hints on recursive decomposition presented earlier in this problem and think again about your strategy.
Your code here:
bool filenameMatches(string filename, string pattern) {
}
Q4) Break Sentence into Dictionary Words (15 Points)
Given a sentence that has no spaces between the words, and a Lexicon of words, write a function to print out all possible combinations of valid words:
void breakSentence(Lexicon &lex, string str);
For example, breakSentence(lex, "subvertexitingot"); would output the
following, given a standard English dictionary:
sub vertex i tin got
sub vertex it in got
sub vertex it ingot
subvert exit in got
subvert exit ingot
Notes:
- You may define helper functions to solve this problem.
- For full credit, your solution must be recursive.
Your code here:
void breakSentence(Lexicon &lex, string str) {
};
Q5) Hash Map (15 Points)
Simulate the behavior of a hash map of ints (keys) to strings (values). This map will function like the hash set as described in lecture, but it stores key/value pairs rather than just keys. Assume the following:
- the hash map array has an initial capacity of 10.
- the hash map uses linked list chaining to resolve collisions, and key/value pairs are inserted at the head of each linked list.
- the hash/compression function is defined as follows:
int hash(int key) { return key % tableCapacity; }notice that the function does not depend on the value, only the key.
- rehashing occurs at the end of a
putwhere the load factor is >= 1.0 and doubles the capacity of the hash map. Rehashing should be performed as discussed in lecture.
Draw an array diagram to show the final state of the hash map after the following operations are performed. You may leave unused buckets blank, assuming they will contain nullptr. All values must be in the proper buckets and in the proper order to receive full credit. Also write the final number of elements, capacity, and load factor of the hash map.
map.put(10,"perform");
map.put(20,"your");
map.put(15,"banana");
map.put(53,"get");
map.put(51,"will");
map.put(13,"full");
map.put(106,"106b");
map.put(6,"map");
map.put(87,"skills");
map.remove(10);
map.put(27,"are");
map.put(40,"hash");
map.remove(106);
map.put(28,"and");
map.put(88,"fantastic");
map.put(78,"credit");
map.put(29,"you");
map.remove(15);
Your finished table might look something like this:
0: 15,banana -> 88,fantastic -> 40,hash
1:
2: 28,and
3: 6,map -> 78,credit
4:
5:
6: 29,you
etc.
Final number of elements: 7
Capacity: 10
Load factor: 0.7
Q6) Backtracking: All Paths from Start to Finish (15 points)
Given a Grid of bools, g, write a function allPaths that returns a Vector of strings of all possible paths to traverse from the top left corner of the grid (row=0, col=0) to the bottom right corner of the grid (row=g.numRows()-1, col=g.numCols()-1), without re-visiting any grid locations. A path string is defined as a string of compass directions, 'n', 'e', 's', and 'w' corresponding to north, east, south, and west.
Vector<string> allPaths(Grid<bool> &g);
You are allowed to create any helper functions you need, and your solution should recursively produce all possible paths as described.
For example, for a 4x4 grid below, the path "eeeswses" is drawn on the left grid, and the path "ssseenes" is drawn on the right grid.
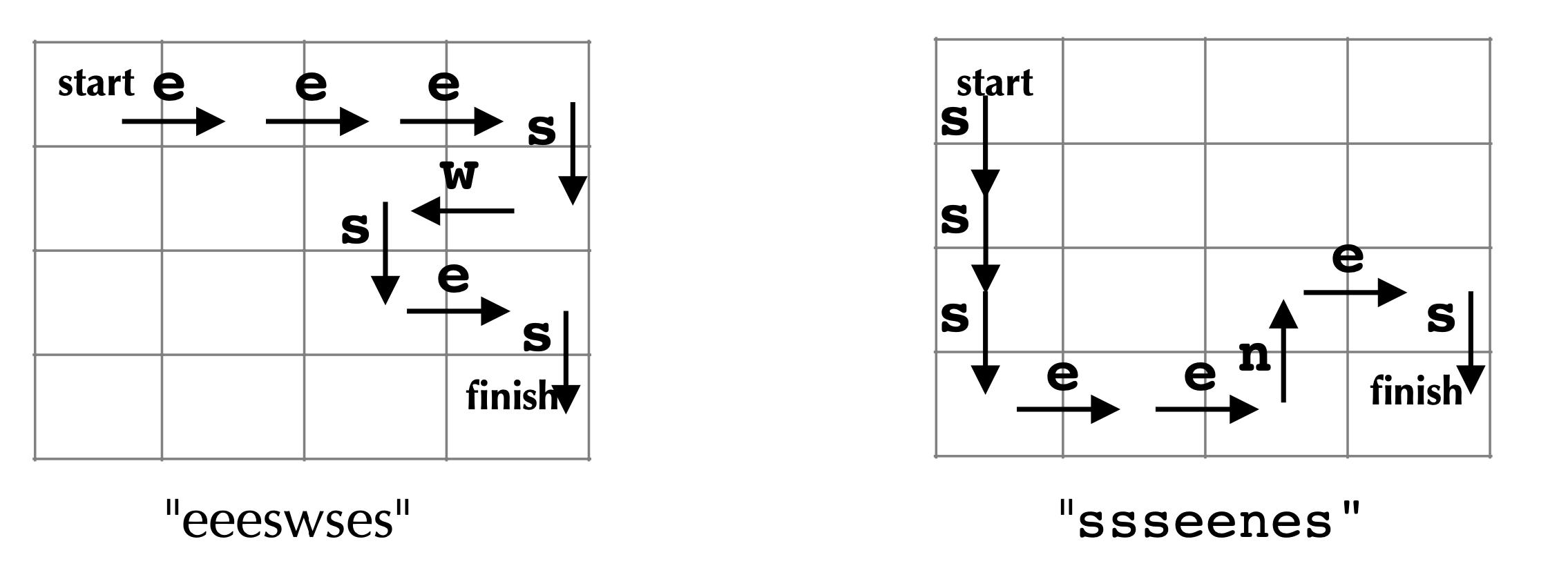
Notes:
- The initial Grid passed into the function will have all of its elements marked as "
false". - The Grid is guaranteed to be at least 1x1 in size (and a 1x1 grid has "" as the path).
- You should probably use the boolean values in the grid to mark where you have been in the grid as you complete your recursive function. A particular path should not revisit any grid locations.
- You must use recursion to receive full credit.
Your code here
Vector<string> allPaths(Grid<bool> &g) {
}