Abstract

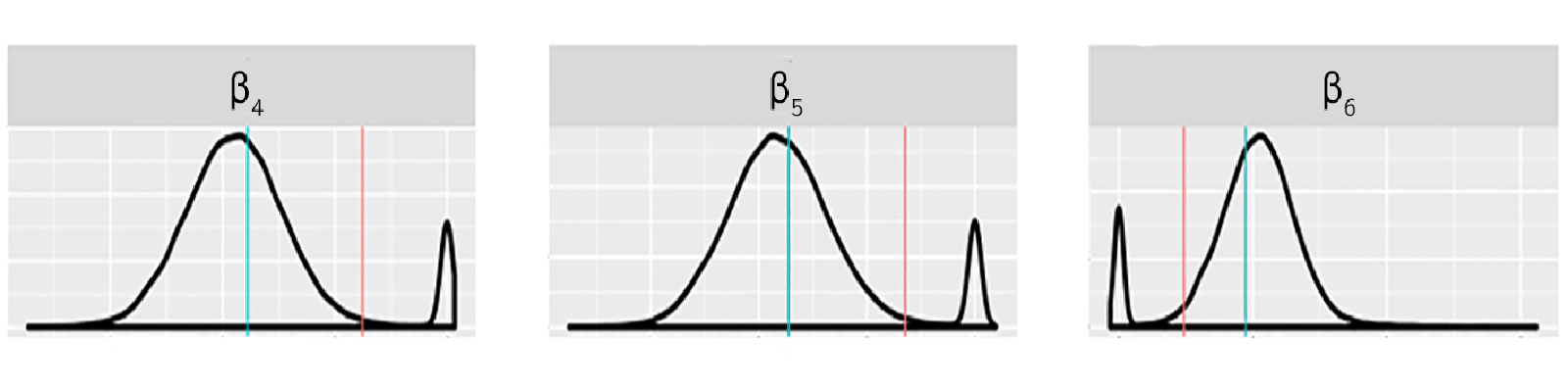
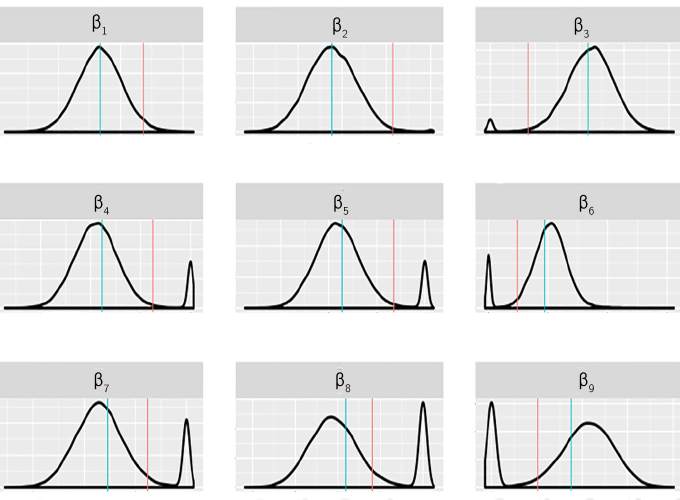
We propose two new MCMC algorithms for the Horseshoe prior, one of the main Bayesian models for sparse high-dimensional regression, that have improved performance compared to existing alternatives. One of the algorithms also approximates an expensive matrix product to give orders of magnitude speedup in high-dimensional applications. We prove the exact algorithm is geometrically ergodic, and give guarantees for the accuracy of the approximate algorithm using perturbation theory. We consider an application to a genome-wide association study with $N=2,267$ and $p=98,385$. The empirical results show that the new algorithm yields estimates with lower mean squared error, intervals with better coverage, and elucidates features of the posterior that were often missed by previous algorithms in high dimensions, including bimodality of posterior marginals indicating uncertainty about which covariates belong in the model.