Algorithm
We consider linear regression model, where we are given 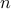 i.i.d. pairs
i.i.d. pairs 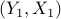 ,
, 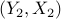 ,
,  ,
, 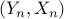 with vectors
with vectors 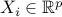 and response variables
and response variables 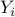 are given by
are given by
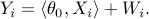
Here 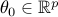 is the vector of coefficients,
is the vector of coefficients, 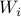 is measurement noise with mean zero and variance
is measurement noise with mean zero and variance 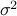 . Moreover,
. Moreover, 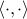 denotes the standard scalar product in
denotes the standard scalar product in 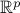 .
.
In matrix form, letting 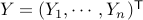 and denoting by
and denoting by 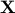 the design matrix with rows
the design matrix with rows 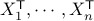 , we have
, we have
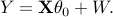
Note: We are primarily interested in high-dimensional regime, where the number of parameters is larger than the number of samples 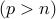 , although our method applies to the classical low-dimensional setting
, although our method applies to the classical low-dimensional setting 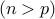 as well.
as well.
Given response vector 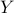 and design matrix
and design matrix 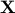 , we want to construct confidence intervals for each single coefficient
, we want to construct confidence intervals for each single coefficient 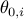 .
.
Furthermore, we are interested in testing individual null hypothesis 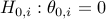 versus the alternative
versus the alternative 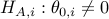 , and assigning
, and assigning  -values for these tests.
-values for these tests.
Method:
Here, we provide a simple explanation of our method. For more details and discussions, please see our paper.
Our method is based on constructing a ‘de-biased’ version of LASSO.
Let 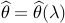 be the LASSO estimator with regularization parameter
be the LASSO estimator with regularization parameter 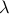 . For a matrix
. For a matrix 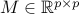 , define
, define
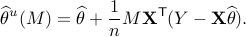
For a suitable choice of matrix 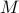 , we characterize distribution of the de-biased estimator
, we characterize distribution of the de-biased estimator 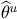 , from which we construct asymptotically valid confidence intervals, as follows:
, from which we construct asymptotically valid confidence intervals, as follows:
For 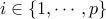 and significance
and significance 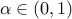 , we let
, we let
![J_i(alpha) ,,,, equiv,, [widehat{theta}^u_i - delta(alpha,n), widehat{theta}^u_i + delta(alpha,n)],](eqs/1739838698-130.png)
![delta(alpha,n) equiv ,, Phi^{-1}(1-alpha/2) frac{widehat{sigma}}{sqrt{n}} [Mwidehat{Sigma} M^{sf T}]^{1/2}_{i,i}.](eqs/1920921733-130.png)
Here, 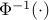 is the quantile function of the standard normal distribution and
is the quantile function of the standard normal distribution and 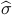 is a consistent estimator of
is a consistent estimator of 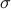 .
.
For testing the null hypothesis 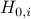 , we construct a two-sided
, we construct a two-sided  -value as follows:
-value as follows:
![P_i = 2left(1-Phileft(frac{sqrt{n}|widehat{theta}^u_i|}{widehat{sigma} [Mwidehat{Sigma} M^{sf T}]^{1/2}_{i,i}}right)right).](eqs/126536164-130.png)
How to choose matrix M?
For input parameter 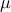 , the de-biasing matrix
, the de-biasing matrix 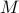 is constructed via the following optimization problem:
is constructed via the following optimization problem:
1. for 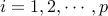 do
do
Let 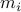 be a solution of the convex program:
be a solution of the convex program:
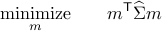
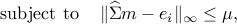
where 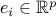 is the vector with one at the
is the vector with one at the 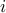 -th position and zero
everywhere else.
-th position and zero
everywhere else.
2. Set 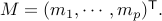 ( Rows of
( Rows of 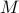 are the vectors
are the vectors 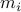 .)
.)
In our code, the user can either give parameters 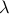 and
and 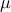 as input or let the algorithm select their values automatically.
as input or let the algorithm select their values automatically.