Illustrate an sRGB standard display reference.

We demonstrate display (sRGB) calculations and how these work with XYZ and linear RGB values. These values are often used when we want to compute how an image would appear on a standard (sRGB) display.

Modern reference: SRGB reference

Create a simple scene of the Macbeth Color Checker

scene = sceneCreate;

Read the xyz data from the MCC and put it in an image format

xyz = sceneGet(scene,'xyz');

Let's have a look

vcNewGraphWin; imagescRGB(xyz);

Convert xyz to srgb

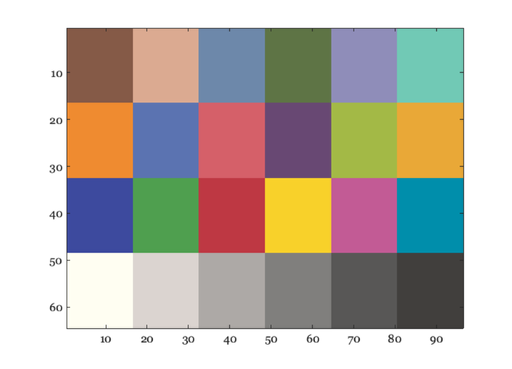
% We find the max Y and normalize xyz when we call the function.  This is
% expected in the standard (see Wikipedia page).
Y = xyz(:,:,2); maxY = max(Y(:))
sRGB = xyz2srgb(xyz/maxY);

% Visualize the result
vcNewGraphWin; image(sRGB)

maxY =

  single

  319.6744

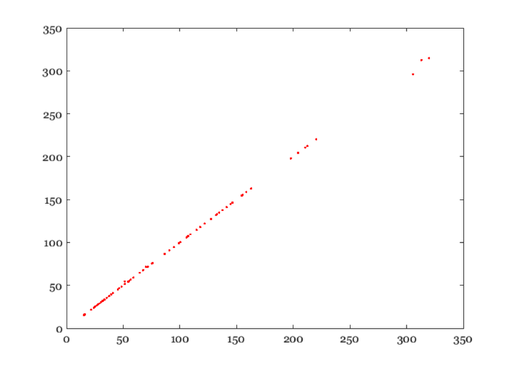
Invert sRGB to XYZ

estXYZ = srgb2xyz(sRGB)*maxY;
vcNewGraphWin; plot(xyz(:),estXYZ(:),'.');

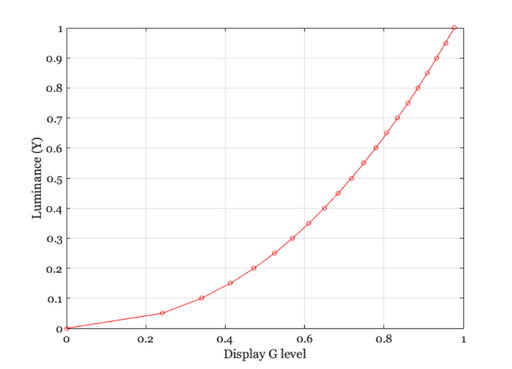
The gamma curve of the sRGB transform, which is about 2.2

% Here is a linear range of XYZ values
v = 0:.05:1;
nRows = length(v);
xyz = repmat(v,3,1); xyz = xyz';
xyz = XW2RGBFormat(xyz,1,nRows);
Y = xyz(1,:,2);

% If you want to have a look:
% imagescRGB(imageIncreaseImageRGBSize(xyz,5));

sRGB = xyz2srgb(xyz);
G = sRGB(1,:,2);
% imagescRGB(imageIncreaseImageRGBSize(sRGB,5));

vcNewGraphWin; plot(G,Y,'-o');
xlabel('Display G level'); ylabel('Luminance (Y)');
grid on

Transform matrix from sRGB to XYZ

colorTransformMatrix('xyz2srgb')
S2X = inv(colorTransformMatrix('xyz2srgb'))

ones(1,3)*S2X

ans =

    3.2410   -0.9692    0.0556
   -1.5374    1.8760   -0.2040
   -0.4986    0.0416    1.0570


S2X =

    0.4124    0.2126    0.0193
    0.3576    0.7151    0.1192
    0.1805    0.0721    0.9505


ans =

    0.9504    0.9999    1.0891