Review rendering images on a display (Psych 221)
Class: Psych 221/EE 362
Tutorial: Examples of rendering images
Author: Wandell
Purpose: Explain how to render illuminant and surface reflectance
data on a screen.
Date: 01.02.96
Duration: 20 minutes
Contents
ieInit
Render the MCC on a monitor (match scanner)
% Load in the surface reflectances of the Macbeth ColorChecker. Also, % we know the color appearance of a few of them so let's give them % labels. % load macbethChart; fName = which('macbethChart.mat'); wave = 400:700; macbethChart = ieReadSpectra(fName,wave); % There are 24 surfaces, so we prepare a small matrix (6 by 4) with 24 % entries. Later, we will use this matrix to display the 24 surfaces. % The way we will do the display is to build a colormap with 24 rows. % Each row will describe the (r,g,b) values for one surface. macbethImage = reshape(1:24,4,6); % We can't display a pure surface. We always need to display a % surface under a particular light. Hence, an important thing to % remember during this rendering exercise is that we have chosen a % particular light. Later, you might come back to this point and load % in a different choice for a light. % For now, load in the D65 illuminant and call it the lgt. lgt = ieReadSpectra('D65',wave); % Load data for a default monitor and the XYZ functions % d = displayCreate('OLED-Samsung','wave',wave); phosphors = displayGet(d,'rgb spd'); XYZ = ieReadSpectra('XYZ',wave);
Render the MCC on a monitor (match XYZ)
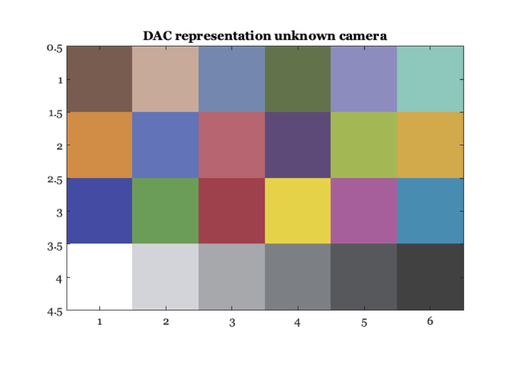
% First, compute the XYZ values of the macbeth colorchecker under the % default illuminant. These values describe how the human visual % system will encode the light reflected from each of the surfaces. % You should check that this calculation makes sense to you by writing % it out as a matrix tableau. Note the use of the diag() function % .... macbethXYZ = XYZ'* diag(lgt)* macbethChart; % Here, we determine the linear RGB settings we will need in order to % create the same XYZ values on the default monitor. Your monitor may % not be the same, of course. macbethLinearRGB = inv(XYZ'*phosphors)*macbethXYZ; % Now, we haven't set any absolute units for this match. For example % we don't know what the absolute intensity of the light source is. % In general, we can't match absolute intensities very well across % viewing conditions. For example, if the surface is outdoors the % outdoor light intensity is several orders of magnitude greater than % the possible output of the monitor. % % So, we are going to ignore the absolute intensities. Instead, we % are simply going to assume that the white surface will be the % brightest element of the image. Consequently, we are going to scale % the RGB values so that the white surface corresponds to the largest % displayable value. macbethLinearRGB = macbethLinearRGB/(max(macbethLinearRGB(:))); % We are representing the relationship between the linear RGB values % and the RGB values in the frame-buffer using a look-up table that % accounts for for the monitor nonlinearity. This lookup table stores % the inverse gamma function, and we have called it monitorInvGam % (both here and in other tutorials). So, let's scale the RGB values % so that they fall within the range set by that table. % Now, we are going to use a trick that people often do -- just a % trick, no deep principles here -- for setting the absolute levels. % We are going to assume that: THE WHITE SURFACE XYZ should % correspond to the MONITOR DISPLAY AT [255,255,255]. This is not % exactly right. In fact, it is not right at all. If you have good % calibration methods, you don't need to do this. But, people rarely % have good calibration methods so they do this. Let's carry on, % though we will talk about this in class. whiteChip = 4; % Here are the RGB settings for the white chip wht = macbethLinearRGB(:,whiteChip); % Scale ALL of the RGB values so that the white chip has a framebuffer % value that is roughly (1,1,1). macbethLinearRGB = diag( (1 ./ wht ) ) * macbethLinearRGB; % Correct for the monitor nonlinearity. iGtable = displayGet(d,'inverse gamma'); RGB = XW2RGBFormat(macbethLinearRGB',4,6); macbethRGB = rgb2dac(RGB,iGtable); % There are 24 chips, and we have computed the proper display % intensities for each one of them. We place an image that consists % of the list of values 1:24, into the frame-buffer. We set the color % table values to the proper r,g,b values. % macbethRGB = macbethRGB/max(macbethRGB(:)); % Now, we put up this 6 x 4 matrix and set the image to have the right % color map. ieNewGraphWin; image(macbethRGB); axis image title('DAC representation unknown camera') % Voila.
Render the MCC on a monitor (match rgb)
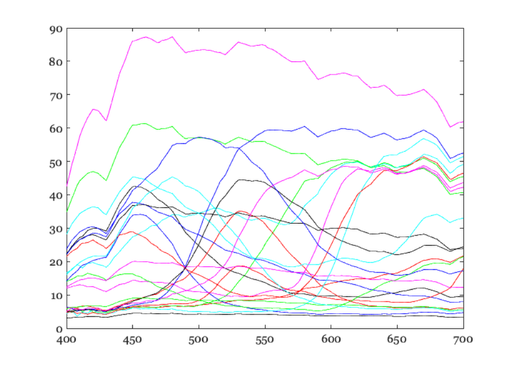
% Now, suppose that you don't know very much about either the display % or, say, a digital camera that you used to acquire the data you want % to display. What do you do? % Here, we are going to make some simulated rgb data from a digital % camera. The strategy we will use to match the display and the % original image is to MEASURE THE DISPLAY OUTPUT WITH THE DIGITAL % CAMERA. Then, we will try to adjust the display output so that it % causes the same RGB signal at the camera as the original macbeth % Color Checker image. % Once again, we compute the color signal from the color checker under % some light. colorSignal = diag(lgt)*macbethChart; ieNewGraphWin; plot(wave,colorSignal) % For this simulation, we calculate the expected camera rgb signals % from each of the color signals. sensors = ieReadSpectra('cMatch/camera', wave); cameraRGB = sensors'* colorSignal; % Next, we need to know how the camera would respond to light from % each of the monitor phosphors. This will permit us to build a % matrix that converts from the linear monitor intensities to the % camera RGB responses. We will call this matrix mon2camera. This % will be a 3 x 3 matrix. The first column describes the RGB values % when the red phoshor is on, the second and third when the green and % blue are on respectively. % Experimentally, we could obtain these values just by taking a camera % picture of the monitor. For example, suppose we just turn on the % red phosphor, and we use the camera to take a picture of the red % phosphor. % In this case, though, we know the sensors. So, rather than asking % you to do the experiment (but do it if you would like). However % given that we know the sensors, we can compute this matrix simply % as: mon2camera = sensors'*phosphors; % This tells us how to set the monitor (linear) RGB values in order to % match a set of (linear) CAMERA RGB values. N.B. The human eye is % not involved in this calculation. We are adjusting the monitor % output so that the camera will have the same responses. There is no % mention of people, CIE standards, or the like in any of this % calculation. camera2mon = inv(mon2camera) % We now use the matrix camera2mon to compute the display rgb values macbethCameraLinearRGB = camera2mon*cameraRGB; % Again, to make a decent picture we will need to correct for the % framebuffer nonlinearity. And, we don't really have much choice % about the absolute intensity of various quantities. So, let's % perform the same set of calculations we did before in order to % render a display. macbethCameraLinearRGB = ... round(1000*macbethCameraLinearRGB/(max(macbethCameraLinearRGB(:)))); % Because we don't really know the properties of this display, we are % going to arrange things so that the known white chip is displayed as % the white of the monitor. This is a cheap trick that often makes % people and managers happy. % wht = macbethCameraLinearRGB(:,whiteChip); macbethCameraLinearRGB = diag( (1 ./ wht ) ) * macbethCameraLinearRGB; % macbethCameraLinearRGB = ieScale(macbethCameraLinearRGB,1,size(iGtable,1)); macbethCameraLinearRGB = ieScale(macbethCameraLinearRGB,1); macbethCameraRGB = rgb2dac(macbethCameraLinearRGB',iGtable); % There are 24 chips, and we have computed the proper display % intensities for each one of them. We place an image that consists % of the list of values 1:24, into the frame-buffer. We set the color % table values to the proper r,g,b values. % macbethCameraColorMap = ieScale(macbethCameraRGB,1); ieNewGraphWin; colormap(macbethCameraColorMap) image(macbethImage); axis image title(sprintf('Rendered for simulated camera.'))
camera2mon = 76.2953 -1.4488 -0.5081 -0.7640 79.0383 -4.1413 -0.0857 -1.9754 82.5339