Convert between energy and quanta using Planck's relation

Explain the relationship between units of energy and units of quanta (photons). These differences matter for calculations involving the CIE functions and human cone quantum absorptions

References: The photons and energy are connected by Planck's Relation

  photons = (energy/(h*c)) .* wavelength);
  energy  = (h*c) * photons ./ wavelength;

The term h is Planck's constant and c is the speed of light.

ISET stores these constants so you can find them:

  vcConstants('plancks constant')
  vcConstants('speed of light')

Show the wavelength dependency of the conversion from energy to photons
The spectral power distribution (SPD) in energy and quanta
Energy, Photons, and the CIE XYZ functions
Calculating XYZ for a D65 light
CIE Luminance (Y)
End

ieInit

Show the wavelength dependency of the conversion from energy to photons

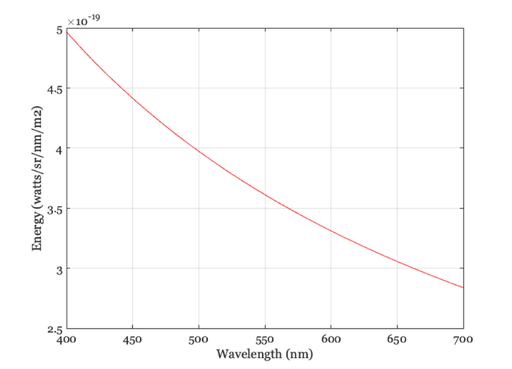
% We can calculate the energy for quanta at different wavelengths by
% setting up a vector of 1s to represent the photons and then calling
% function  Quanta2Energy
wave = 400:5:700;
photons = ones(length(wave),1);
E = Quanta2Energy(wave,photons);

% Notice that the amount of energy per photon declines with longer
% wavelengths.
vcNewGraphWin; plot(wave,E); grid on
xlabel('Wavelength (nm)');ylabel('Energy (watts/sr/nm/m2)')

The spectral power distribution (SPD) in energy and quanta

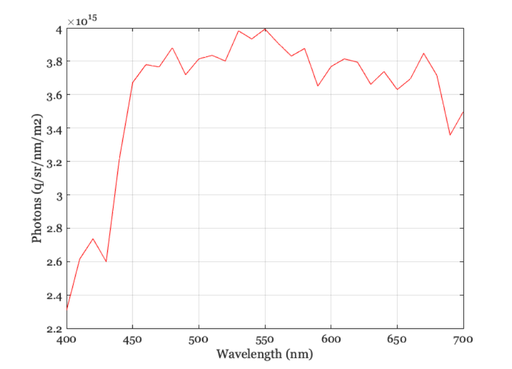
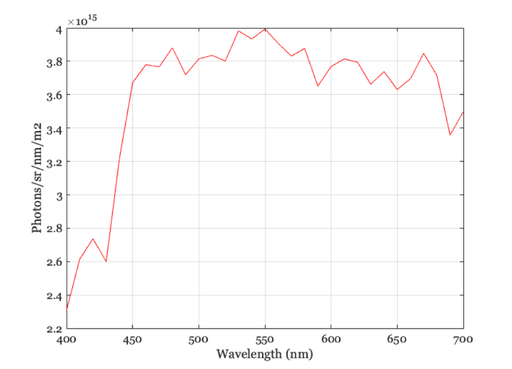
% This is a standard Daylight 6500 light source.  We read it and set its
% luminance to 100 cd/m2.
d65Energy = ieReadSpectra('D65.mat',wave);
d65XYZ    = ieXYZFromEnergy(d65Energy(:)',wave);
d65Energy = d65Energy*100/d65XYZ(2);

% Have a look at the SPD and note the energy levels
vcNewGraphWin; plot(wave,d65Energy); grid on
xlabel('Wavelength (nm)');ylabel('Energy (watts/sr/nm/m2)')

% Next, convert the light from energy units to photons.
d65Photons = Energy2Quanta(wave(:),d65Energy(:));

% Look at the number of photons emitted from the source per square meter
% and per steradian.  Notice that the overall shape of the curves differ
% with the fall off at longer wavelengths is more rapid for energy than for
% photons.  That is, the D65 light has about the same number of long
% (650nm) and middle (550nm) wavelength photons.  But there is more energy
% in the middle wavelength photons.
%
vcNewGraphWin; plot(wave,d65Photons); grid on
xlabel('Wavelength (nm)'); ylabel('Photons (q/sr/nm/m2)')

Energy, Photons, and the CIE XYZ functions

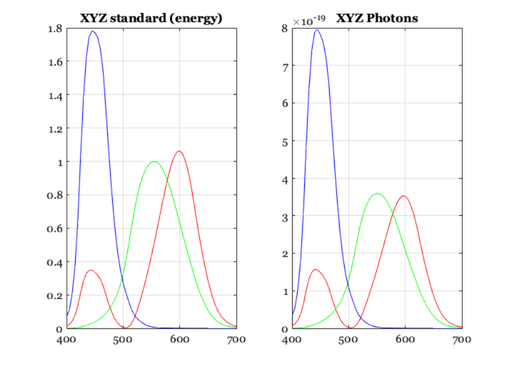
% The CIE 1931 standard curves for XYZ are defined assuming that the input
% signal is specified in terms of energy.
XYZEnergy = ieReadSpectra('XYZ',wave);
vcNewGraphWin;
subplot(1,2,1), plot(wave,XYZEnergy); grid on; title('XYZ standard (energy)');

% For good reasons, the ISET sensor calculations are based on a
% representation of the input signal in photons.  If you wish to use an XYZ
% filter on a sensor and want the output voltage to measure the XYZ value
% of a light, then the filter used by the sensor should expect the input
% signal to be defined in photons, not energy.  You can see how to adjust
% the filter by examining the ISET script, XYZQuanta.m.
% type XYZQuanta.m
XYZPhotons = ieReadSpectra('XYZQuanta',wave);
subplot(1,2,2), plot(wave,XYZPhotons); grid on; title('XYZ Photons')

Calculating XYZ for a D65 light

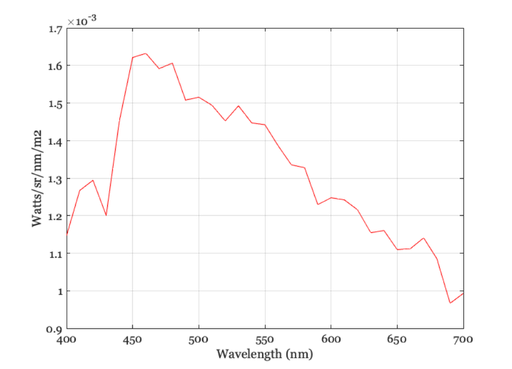
% We read a standard light (Daylight 6500 K) and scale it to have a
% luminance of 100 cd/m2.
d65Energy = ieReadSpectra('D65',wave);
d65XYZ    = ieXYZFromEnergy(d65Energy(:)',wave);
d65Energy = d65Energy*100/d65XYZ(2);

% Have a look at the SPD and note the energy levels
vcNewGraphWin; plot(wave,d65Energy); grid on
xlabel('Wavelength (nm)');ylabel('Watts/sr/nm/m2')

% Next, convert the light from energy units to photons.
d65Photons = Energy2Quanta(wave(:),d65Energy(:));
vcNewGraphWin; plot(wave,d65Photons); grid on
xlabel('Wavelength (nm)');ylabel('Photons/sr/nm/m2')

% The proper filters will be used when you calculate XYZ with the proper
% functions, such as:
d65XYZ = ieXYZFromPhotons(d65Photons(:)',wave)
d65XYZ = ieXYZFromEnergy(d65Energy(:)',wave)

d65XYZ =

   94.9402  100.0000  108.6629


d65XYZ =

   94.9402  100.0000  108.6629

CIE Luminance (Y)

For those of you interested, the relationship between the XYZ curves and the luminance level (Y) is a simple relationship:

dnm = wave(2)-wave(1);   % Wavelength step
% The 683 value is a constant used by the CIE having to do with certain
% material standards.  The two formula return the same values
d65XYZ = dnm*683*XYZPhotons'*d65Photons(:)
d65XYZ = dnm*683*XYZEnergy'*d65Energy(:)