Mixing Times for Random Walks on Geometric Random Graphs
SIAM Workshop on Analytic Algorithmics & Combinatorics (ANALCO), Vancouver, January 2005.
A geometric random graph, 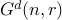 , is formed as follows: place
, is formed as follows: place 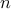 nodes
uniformly at random onto the surface of the
nodes
uniformly at random onto the surface of the 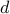 -dimensional unit torus and
connect nodes which are within a distance
-dimensional unit torus and
connect nodes which are within a distance  of each other.
The
of each other.
The 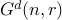 has been of great interest due to its success as a model for ad-hoc wireless
networks. It is well known that the connectivity of
has been of great interest due to its success as a model for ad-hoc wireless
networks. It is well known that the connectivity of 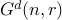 exhibits a
threshold property: there exists a constant
exhibits a
threshold property: there exists a constant 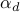 such that for any
such that for any
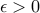 , for
, for 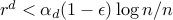 , the
, the 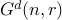 is not
connected with high probability, and for
is not
connected with high probability, and for 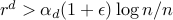 , the
, the 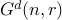 is connected w.h.p.
In this paper, we study mixing properties
of random walks on
is connected w.h.p.
In this paper, we study mixing properties
of random walks on 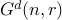 for
for 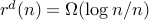 .
Specifically, we
study the scaling of mixing times of the fastest-mixing reversible random walk,
and the natural random walk. We find that the mixing time of both of these
random walks have the same scaling laws and scale proportional to
.
Specifically, we
study the scaling of mixing times of the fastest-mixing reversible random walk,
and the natural random walk. We find that the mixing time of both of these
random walks have the same scaling laws and scale proportional to
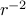 (for
all
(for
all 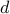 ). These results hold for
). These results hold for 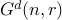 when distance is defined
using any
when distance is defined
using any 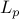 norm. Though the results of this paper are
not so surprising, they are
nontrivial and require new methods. To obtain the scaling law for the
fastest-mixing reversible random walk, we first explicitly characterize the
fastest-mixing reversible random walk on a regular (grid-type) graph in
norm. Though the results of this paper are
not so surprising, they are
nontrivial and require new methods. To obtain the scaling law for the
fastest-mixing reversible random walk, we first explicitly characterize the
fastest-mixing reversible random walk on a regular (grid-type) graph in 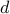 dimensions. We subsequently use this to bound the mixing time of the
fastest-mixing random walk on
dimensions. We subsequently use this to bound the mixing time of the
fastest-mixing random walk on 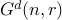 . In the course of our analysis, we
obtain a tight relation between the mixing time of the fastest-mixing symmetric
random walk and the fastest-mixing reversible random walk with a specified
equilibrium distribution on an arbitrary graph. To study the natural random
walk, we first generalize a method of Diaconis and Stroock (1991) to bound
eigenvalues based on Poincare's inequality and then apply it to the
. In the course of our analysis, we
obtain a tight relation between the mixing time of the fastest-mixing symmetric
random walk and the fastest-mixing reversible random walk with a specified
equilibrium distribution on an arbitrary graph. To study the natural random
walk, we first generalize a method of Diaconis and Stroock (1991) to bound
eigenvalues based on Poincare's inequality and then apply it to the
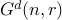 graph.
graph.