Contents

% L1 regularized logistic regression (not distributed)

Generate problem data

rand('seed', 0);
randn('seed', 0);

n = 50;
m = 200;

w = sprandn(n, 1, 0.1);  % N(0,1), 10% sparse
v = randn(1);            % random intercept

X = sprandn(m, n, 10/n);
btrue = sign(X*w + v);

% noise is function of problem size use 0.1 for large problem
b = sign(X*w + v + sqrt(0.1)*randn(m,1)); % labels with noise

A = spdiags(b, 0, m, m) * X;

ratio = sum(b == 1)/(m);
mu = 0.1 * 1/m * norm((1-ratio)*sum(A(b==1,:),1) + ratio*sum(A(b==-1,:),1), 'inf');

x_true = [v; w];

Solve problem

[x history] = logreg(A, b, mu, 1.0, 1.0);

iter	    r norm	   eps pri	    s norm	  eps dual	 objective
  1	    3.3583	    0.0489	    2.9421	    0.0343	     31.57
  2	    1.5574	    0.0439	    1.8655	    0.0469	     40.27
  3	    0.9098	    0.0469	    0.8803	    0.0530	     43.50
  4	    0.6102	    0.0489	    0.4102	    0.0573	     44.71
  5	    0.4396	    0.0499	    0.1878	    0.0602	     45.56
  6	    0.3283	    0.0503	    0.0802	    0.0624	     46.12
  7	    0.2521	    0.0504	    0.0318	    0.0641	     46.51
  8	    0.1979	    0.0505	    0.0133	    0.0654	     46.79
  9	    0.1580	    0.0505	    0.0083	    0.0663	     46.99
 10	    0.1201	    0.0505	    0.0220	    0.0671	     47.18
 11	    0.0916	    0.0505	    0.0358	    0.0676	     47.34
 12	    0.0719	    0.0505	    0.0133	    0.0679	     47.42
 13	    0.0575	    0.0505	    0.0060	    0.0683	     47.47
 14	    0.0463	    0.0505	    0.0037	    0.0685	     47.52
Elapsed time is 0.093047 seconds.

Reporting

K = length(history.objval);

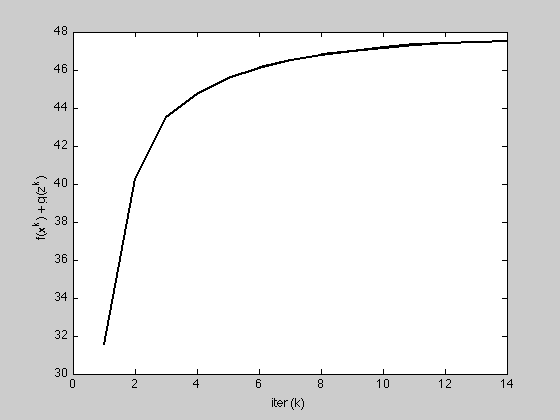
h = figure;
plot(1:K, history.objval, 'k', 'MarkerSize', 10, 'LineWidth', 2);
ylabel('f(x^k) + g(z^k)'); xlabel('iter (k)');

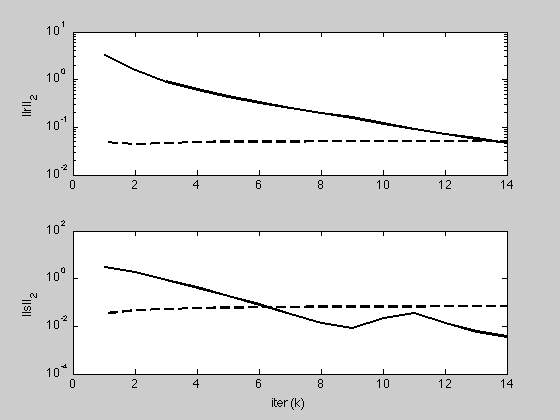
g = figure;
subplot(2,1,1);
semilogy(1:K, max(1e-8, history.r_norm), 'k', ...
    1:K, history.eps_pri, 'k--',  'LineWidth', 2);
ylabel('||r||_2');

subplot(2,1,2);
semilogy(1:K, max(1e-8, history.s_norm), 'k', ...
    1:K, history.eps_dual, 'k--', 'LineWidth', 2);
ylabel('||s||_2'); xlabel('iter (k)');

Published with MATLAB® 7.7