Contents
Generate problem data
randn('state', 0);
rand('state', 0);
n = 500;
m = 400;
c = rand(n,1) + 0.5;
x0 = abs(randn(n,1));
A = abs(randn(m,n));
b = A*x0;
Solve problem
[x history] = linprog(c, A, b, 1.0, 1.0);
iter r norm eps pri s norm eps dual objective
1 1.0583 0.2090 20.6468 0.0128 377.17
2 1.3281 0.2132 2.2600 0.0253 371.25
3 1.5087 0.2182 1.9352 0.0387 367.10
4 1.5695 0.2229 1.6421 0.0518 364.81
5 1.5312 0.2262 1.4066 0.0635 364.21
6 1.4058 0.2280 1.2723 0.0733 364.81
7 1.2277 0.2286 1.2189 0.0807 365.98
8 1.0224 0.2286 1.2002 0.0859 367.35
9 0.8861 0.2282 1.1314 0.0887 368.77
10 0.8534 0.2278 1.0007 0.0896 370.05
11 0.8526 0.2275 0.8478 0.0893 371.04
12 0.7885 0.2272 0.7667 0.0884 371.69
13 0.7181 0.2271 0.6922 0.0872 372.04
14 0.6492 0.2272 0.6628 0.0859 372.10
15 0.5849 0.2274 0.6356 0.0848 371.97
16 0.5359 0.2276 0.5851 0.0839 371.76
17 0.4933 0.2279 0.5560 0.0833 371.53
18 0.4857 0.2279 0.4907 0.0829 371.32
19 0.4840 0.2278 0.4258 0.0827 371.17
20 0.4652 0.2277 0.3954 0.0828 371.06
21 0.3946 0.2276 0.4067 0.0830 370.97
22 0.3540 0.2275 0.3861 0.0833 370.92
23 0.3225 0.2274 0.3638 0.0836 370.92
24 0.3077 0.2274 0.3378 0.0838 370.96
25 0.2989 0.2273 0.3120 0.0839 371.05
26 0.2927 0.2272 0.2886 0.0838 371.15
27 0.2798 0.2272 0.2745 0.0837 371.25
28 0.2677 0.2273 0.2582 0.0835 371.31
29 0.2536 0.2273 0.2492 0.0832 371.34
30 0.2406 0.2274 0.2416 0.0830 371.34
31 0.2309 0.2276 0.2324 0.0828 371.31
32 0.2224 0.2277 0.2225 0.0827 371.27
33 0.2153 0.2279 0.2121 0.0826 371.22
34 0.2020 0.2281 0.2088 0.0825 371.18
35 0.1868 0.2282 0.2054 0.0826 371.14
36 0.1725 0.2283 0.2032 0.0826 371.12
37 0.1643 0.2285 0.1970 0.0826 371.13
38 0.1608 0.2286 0.1869 0.0826 371.15
39 0.1598 0.2286 0.1763 0.0825 371.19
40 0.1610 0.2287 0.1630 0.0824 371.22
41 0.1612 0.2287 0.1517 0.0822 371.25
42 0.1597 0.2287 0.1433 0.0820 371.26
43 0.1572 0.2286 0.1366 0.0819 371.26
44 0.1550 0.2286 0.1304 0.0817 371.25
45 0.1524 0.2286 0.1247 0.0816 371.23
46 0.1481 0.2285 0.1225 0.0816 371.21
47 0.1402 0.2285 0.1220 0.0815 371.19
48 0.1283 0.2285 0.1288 0.0815 371.18
49 0.1182 0.2285 0.1295 0.0815 371.17
50 0.1075 0.2284 0.1336 0.0815 371.17
51 0.1008 0.2284 0.1315 0.0815 371.16
52 0.0979 0.2285 0.1289 0.0815 371.16
53 0.0974 0.2285 0.1249 0.0815 371.15
54 0.0961 0.2286 0.1209 0.0815 371.15
55 0.0937 0.2287 0.1188 0.0815 371.14
56 0.0906 0.2287 0.1166 0.0815 371.12
57 0.0882 0.2288 0.1144 0.0815 371.11
58 0.0883 0.2289 0.1107 0.0815 371.09
59 0.0891 0.2290 0.1056 0.0816 371.07
60 0.0897 0.2291 0.1011 0.0817 371.05
61 0.0893 0.2292 0.0967 0.0818 371.03
62 0.0877 0.2292 0.0942 0.0819 371.03
63 0.0856 0.2292 0.0922 0.0820 371.02
64 0.0835 0.2292 0.0906 0.0821 371.01
65 0.0814 0.2292 0.0892 0.0822 371.01
66 0.0797 0.2292 0.0877 0.0823 371.00
67 0.0786 0.2292 0.0860 0.0825 370.99
68 0.0781 0.2292 0.0837 0.0826 370.97
69 0.0786 0.2292 0.0803 0.0828 370.96
Elapsed time is 5.916882 seconds.
Reporting
K = length(history.objval);
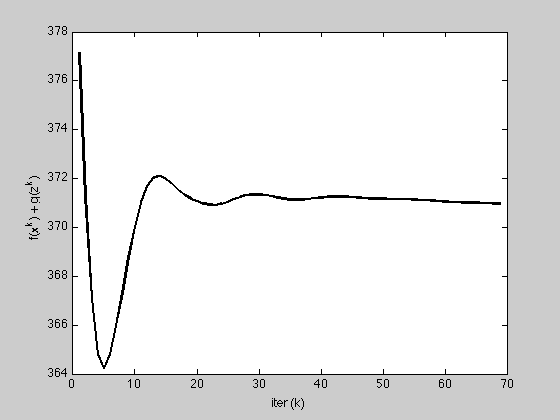
h = figure;
plot(1:K, history.objval, 'k', 'MarkerSize', 10, 'LineWidth', 2);
ylabel('f(x^k) + g(z^k)'); xlabel('iter (k)');
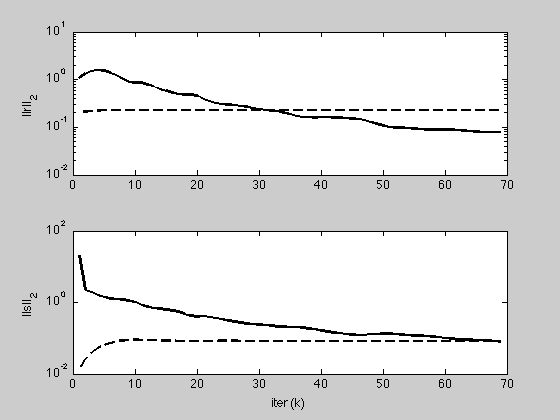
g = figure;
subplot(2,1,1);
semilogy(1:K, max(1e-8, history.r_norm), 'k', ...
1:K, history.eps_pri, 'k--', 'LineWidth', 2);
ylabel('||r||_2');
subplot(2,1,2);
semilogy(1:K, max(1e-8, history.s_norm), 'k', ...
1:K, history.eps_dual, 'k--', 'LineWidth', 2);
ylabel('||s||_2'); xlabel('iter (k)');