Contents

% Huber function fitting example

Generate problem data

randn('seed', 0);
rand('seed',0);

m = 5000;       % number of examples
n = 200;        % number of features

x0 = randn(n,1);
A = randn(m,n);
A = A*spdiags(1./norms(A)',0,n,n); % normalize columns
b = A*x0 + sqrt(0.01)*randn(m,1);
b = b + 10*sprand(m,1,200/m);      % add sparse, large noise

Solve problem

[x history] = huber_fit(A, b, 1.0, 1.0);

iter	    r norm	   eps pri	    s norm	  eps dual	 objective
  1	   15.4154	    0.7767	    5.1477	    0.1556	    642.51
  2	    2.5360	    0.7767	    4.1103	    0.1589	    827.60
  3	    2.2591	    0.7767	    2.1831	    0.1554	    833.26
  4	    1.2350	    0.7767	    1.1045	    0.1544	    832.93
  5	    0.6256	    0.7767	    0.5544	    0.1542	    832.86
  6	    0.3144	    0.7767	    0.2776	    0.1542	    832.87
  7	    0.1575	    0.7767	    0.1389	    0.1542	    832.88
Elapsed time is 0.336020 seconds.

Reporting

K = length(history.objval);

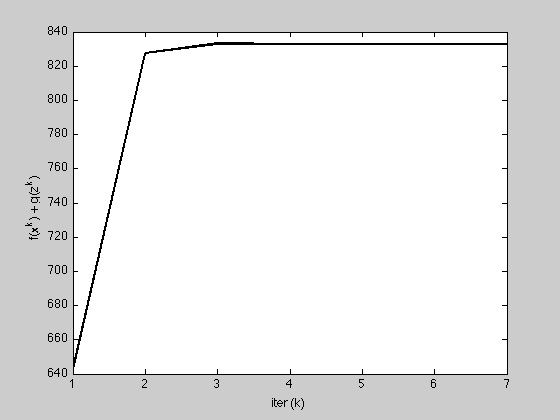
h = figure;
plot(1:K, history.objval, 'k', 'MarkerSize', 10, 'LineWidth', 2);
ylabel('f(x^k) + g(z^k)'); xlabel('iter (k)');

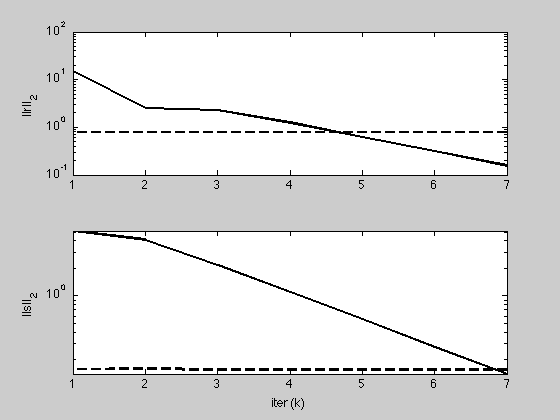
g = figure;
subplot(2,1,1);
semilogy(1:K, max(1e-8, history.r_norm), 'k', ...
    1:K, history.eps_pri, 'k--',  'LineWidth', 2);
ylabel('||r||_2');

subplot(2,1,2);
semilogy(1:K, max(1e-8, history.s_norm), 'k', ...
    1:K, history.eps_dual, 'k--', 'LineWidth', 2);
ylabel('||s||_2'); xlabel('iter (k)');

Published with MATLAB® 7.7