Accuracy at the Top
(Authors listed in alphabetical order.)
NIPS, 2012.
We introduce a new notion of classification accuracy based on the top
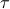-quantile values of a scoring function,
a relevant criterion in a number of
problems arising for search engines. We define an algorithm optimizing a convex
surrogate of the corresponding loss, and show how its solution can be obtained
by solving a set of convex optimization problems. We also present margin-based
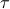guarantees for this algorithm based on the top -quantile of
the scores of the
functions in the hypothesis set. Finally, we report the results of several
experiments in the bipartite setting evaluating the performance of our
algorithm and comparing the results to several other algorithms seeking high
precision at the top. In most examples, our algorithm achieves a better
performance in precision at the top.