File format

Input file format

l1_logreg requires two data files:

feature_file
class_file

feature_file contains the feature matrix for training examples and class_file contains the corresponding class vector of training examples.

Data in feature_file and class_file are stored in Matrix Market (MM) exchange format; see http://math.nist.gov/MatrixMarket/formats.html for more information.

Dense matrix is stored in array format:

%%MatrixMarket matrix array real general
m   n
x₁₁
x₂₁
...
x_m1
x₁₂
x₂₂
...
x_m2
...
x_1n
...
x_mn

The first line contains the header of Matrix Market format. Here, it indicates that the object being represented is a matrix in array format and that the numeric data is real and represented in general form.

The second line contains the number of rows m, and the number of columns n of the feature matrix. From the third row, the matrix is stored in column-oriented order.

Sparse matrix is stored as follows:

%%MatrixMarket matrix coordinate real general
m    n    nnz
i₁   j₁   x_{i1 j1}
i₁   j₂   x_{i1 j2}
    ...
i₂   j₁   x_{i2 j1}
i₂   j₂   x_{i2 j2}
    ...
i_p   j_q   x_{ip jq}

The first line contains the header of Matrix Market format. Here, it indicates that the object being represented is a matrix in coordinate format and that the numeric data is real and represented in general form. The second row contains the number of rows m, the number of columns n and the number of non-zero entries p of the feature matrix. From the third row, the matrix is stored in coordinate format: the first column is the example (row) index, the second column is the feature (column) index, the third column is the corresponding value, of the feature matrix.

Note that the class vector is stored as a matrix in Matrix Market format, whose size is (m x 1). Each class can have a value in [+1,-1]. Here, +1 for positive class, and -1 for negative class.

Output file format

model_file
model_file is generated when l1_logreg_train is executed. It contains a shifted intercept q and normalized coefficients r_i, i=1,...,n. The following vector will be stored in Matrix Market format:
```
%%MatrixMarket matrix array real general
m   1
q
r₁
r₂
...
r_m-1
```
Here, n = m-1.

Without standardization, we can perform classification on a test set X_test

$t =\mbox{sgn}\left(X_{test}w+\mathbf{1}v\right)$

where t is the prediction (or classification result) for the test data set. Thus, q is set to the intercept v and the normalized coefficients are set to the coefficients values, that is, r_i=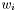 $ w_i $ , i=1,...,n.

When standardization is used, the user need to perform the following:

standardize test example set
apply a linear classifier of intercept and coefficients

This process can be summarized as follows:

$t =\mbox{sgn}\left((X_{test}-\mathbf{1}\mu^T)\mbox{diag}(\sigma)^{-1}w+\mathbf{1}v\right)$

where t is the prediction (or classification result) for the test data set.

For step 1, we need to store the column mean 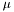$\mu$ and column standard deviation 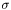$\sigma$ of training example set, and everytime we do classification, we should standardize the test data set. However, this additional effort can be easily avoided by exploiting the property of standardization. We set the normalized coefficients r_i to the coefficients divided by corresponding standard-deviations, that is,

$r=\mbox{diag}(\sigma)^{-1}w.$

Also, the shifted intercept is set to

$q=v-\mu^T\mbox{diag}(\sigma)^{-1}w.$

Then, the classification can be done as follows:

$t =\mbox{sgn}\left(X_{test}r+\mathbf{1}q\right),$

where t is the prediction (or classification result) for the test data set.

result_file
result_file is generated when l1_logreg_classify is executed. The value of t_i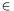 [+1,-1] of ith line corresponds to the classification result of ith example. Here, +1 for positive class, and -1 for negative class.
```
    t₁
    t₂
    ...
    t_m
```

Small example

Consider a small problem with 3 examples and 4 features.

            feature 1   feature 2   feature 3   feature 4       class
example 1      3           0           1          -2             1
example 2      0           0           2           5            -1
example 3      7           1          -4           0             1

Feature file of this problem for dense format is:

%%MatrixMarket matrix array real general
3 4
 3
 0
 7
 0
 0
 1
 1
 2
-4
-2
 5
 0

Feature file for sparse format is:

%%MatrixMarket matrix coordinate real general
3 4 8
1 1  3
3 1  7
3 2  1
1 3  1
2 3  2
3 3 -4
1 4 -2
2 4  5

Class file for both dense and sparse format is:

%%MatrixMarket matrix array real general
3 1
 1
-1
 1

Writing matrices in Matrix Market format

You may directly write matrices in Matrix Market format using any editor or C programs. Also, various software packages are available for reading and writing matrices in Matrix Market format; see http://math.nist.gov/MatrixMarket/formats.html#MMformat.

Writing matrices in Matrix Market format using Matlab

Feature matrices and outcome (class) vectors can be easily written in Matrix Market format within Matlab.

For example, the problem data of the above example can be stored to files by typing the following script in Matlab:

    >> X = [3 0 1 -2; 0 0 2 5; 7 1 -4 0];
    >> b = [1; -1; 1];
    >> mmwrite('exd_simple_X',X);
    >> mmwrite('exd_simple_b',b);

This sequence of commands will generate a dense feature matrix exd_simple_X and the corresponding class vector exd_simple_b.

Sparse matrix can be written to a file in a similar way:

    >> X = [3 0 1 -2; 0 0 2 5; 7 1 -4 0];
    >> b = [1; -1; 1];
    >> X = sparse(X);
    >> mmwrite('exs_simple_X',X);
    >> mmwrite('exs_simple_b',b);

This sequence of commands will generate a sparse feature matrix exs_simple_X and the corresponding class vector exs_simple_b.