elmore_straight

% Elmore delay sizing for a straight wire.
% (a figure of area-delay tradeoff is generated)
%
% This is an example taken from the EE364 lecture notes:
%
%   "Problems in VLSI design" lecture by Prof. Boyd
%   Available at: http://www.stanford.edu/class/ee364
%
% We consider the problem of finding optimal width profile
% for a straight wire segmented into N parts. We want to
% minimize the Elmore delay, subject to limits on wire width
% and the total area. We use a pi-model for each wire segment.
% Problem can be formulated as GP:
%
%   minimize   D
%       s.t.   w_min <= w <= w_max
%              area  <= Amax
%
% where variables are widths w (and arrival times T that are used
% to formulate the overall delay D expression).
%
% Important: We label root node as 1, and all the other nodes as
%            node_label_in_the_paper + 1 (due to Matlab's convention).
%            Also label nodes with increasing numbers downstream.
%
% Almir Mutapcic 02/01/2006
clear all; close all;
PLOT_TRADEOFF = 1; % to disable set PLOT_TRADEOFF = 0;

%********************************************************************
% user supplied data (problem constants and tree topology)
%********************************************************************
N = 10+1; % number of segment (including the root node which is labeled as 1)

% parent node array for the straight wire
% specifies which node is a unique parent for node i (always have a tree)
parent = [0:N-1];

% problem constants
Rsource = 0.1;
l = 1*ones(N-1,1);
alpha = 1*ones(N-1,1);
beta  = 1*ones(N-1,1);
gamma = 1*ones(N-1,1);

% load capacitance at each node
Cload = [0; ones(N-1,1)];

% minimum and maximum width and area specification
Wmin = 1;
Wmax = 10;
Amax = 50;

%********************************************************************
% derived data (computed from user's data)
%********************************************************************
% compute children cell array (evaluate who are children for each node)
children = cell(N,1);
leafs = [];
for node = [1:N]
  children{node} = find(parent == node);
  if isempty(children{node})
    leafs(end+1) = node; % leafs have no children
  end
end

%********************************************************************
% optimization
%********************************************************************
% optimization variables
gpvar w(N-1)     % wire width
gpvar T(N)       % arrival time (Elmore delay to node i)

% wire segment resistance is inversely proportional to widths
R = alpha.*l./w;
R = [Rsource; R];

% wire segment capacitance is an affine function of widths
C_bar = beta.*l.*w + gamma.*l;
C_bar = [0; C_bar];

% compute common capacitances for each node (C_tilde in GP tutorial)
C_tilde = posynomial; % initialize an empty posynomial
for node = [1:N]
  C_tilde(node,1) = Cload(node);
  for k = parent(node)
    if k > 0; C_tilde(node,1) = C_tilde(node,1) + C_bar(k); end;
  end
  for k = children{node}
    C_tilde(node,1) = C_tilde(node,1) + C_bar(k);
  end
end

% now compute total downstream capacitances
C_total = posynomial; % initialize an empty posynomial
for node = N:-1:1
  C_total(node,1) = C_tilde(node);
  for k = children{node}
    C_total(node,1) = C_total(node,1) + C_total(k,1);
  end
end

% generate Elmore delay constraints
elm_delay_constr = [R(1)*C_total(1) <= T(1,1)];
for node = 2:N
  elm_delay_constr = [elm_delay_constr; ...
                      R(node)*C_total(node) + T(parent(node),1) <= T(node,1)];
end

% collect all the constraints
area = sum(w.*l);
constr(1) = area <= Amax;
constr = [constr; Wmin*ones(N-1,1) <= w; w <= Wmax*ones(N-1,1)];
constr = [constr; elm_delay_constr];

% objective is the critical Elmore delay
D = max( T(leafs) );

% solve the problem
[D_value, solution, status] = gpsolve(D, constr);
assign(solution);

% save for plotting
ckt_delay_plot = D_value;
Amax_plot = Amax;

fprintf(1,'\nOptimal Elmore delay for Amax = %d is %3.4f.\n', ...
        Amax, D_value)
disp('Optimal wire widths are: '), w

%********************************************************************
% tradeoff curve code
%********************************************************************
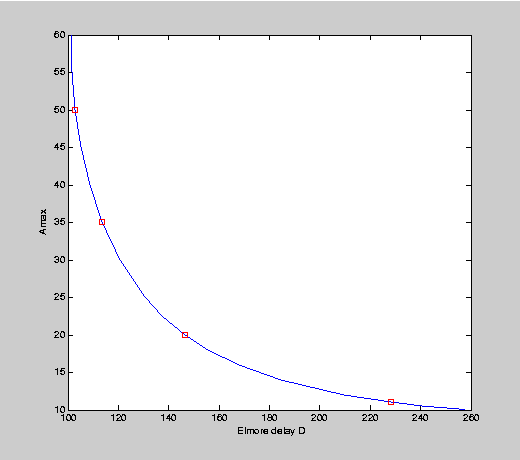
if( PLOT_TRADEOFF )

% set the quiet flag (no solver reporting)
global QUIET; QUIET = 1;

disp('generating the tradeoff curve')
Darray = []; widths = [];
for Amax = [10.01 10.05 10.5 11 12:2:20 22.5 25:5:60]
  % formulate the GP problem and solve it
  constr(1) = area <= Amax;
  [D_value, solution, status] = gpsolve(D, constr);
  Darray = [Darray D_value];
  widths = [widths solution{2,2}];
end

% enable solver reporting again
global QUIET; QUIET = 0;

% indices of four taper designs on the tradeoff curve
Amax = [10.01 10.05 10.5 11 12:2:20 22.5 25:5:60];
A11ind = find(Amax == 11);
A20ind = find(Amax == 20);
A35ind = find(Amax == 35);
A50ind = find(Amax == 50);

% plot the tradeoff curve
plot(Darray,Amax, ...
     Darray(A11ind),Amax(A11ind),'ro',...
     Darray(A20ind),Amax(A20ind),'ro',...
     Darray(A35ind),Amax(A35ind),'ro',...
     Darray(A50ind),Amax(A50ind),'ro');
xlabel('Elmore delay D'); ylabel('Amax');

% plot four taper designs
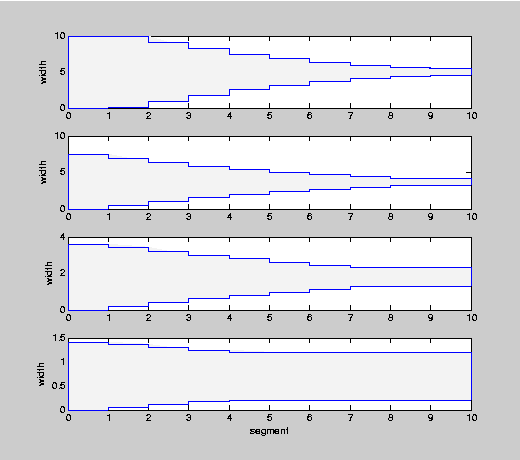
w1 = widths(:,A50ind);
w2 = widths(:,A35ind);
w3 = widths(:,A20ind);
w4 = widths(:,A11ind);
plot_four_tapers(w1,w2,w3,w4);

end
% end tradeoff curve code

 
Iteration     primal obj.         gap        dual residual     previous step.
 
   1         4.85015e+00       7.40000e+01       9.86e+01               Inf
   2         6.07014e+00       2.94834e+01       7.42e-02       9.71831e-01
   3         5.09861e+00       2.14647e+01       1.84e-02       5.00000e-01
   4         4.26896e+00       1.51088e+01       2.68e-04       8.88502e-01
   5         9.84589e-01       7.44638e+00       1.19e-05       1.00000e+00
   6        -4.41937e-02       3.71732e+00       6.24e-08       1.00000e+00
 
Iteration     primal obj.         gap        dual residual     previous step.
 
   1         1.99451e+02       7.40000e+01       1.02e+00               Inf
   2         1.69615e+02       7.11239e+01       9.38e-01       4.30026e-02
   3         1.14054e+02       6.84579e+01       8.82e-01       3.05167e-02
   4         5.21557e+01       6.32546e+01       7.82e-01       5.84731e-02
   5         1.00365e+01       5.51294e+01       6.07e-01       1.26306e-01
   6         9.00984e+00       3.62474e+01       1.44e-02       1.00000e+00
   7         7.22206e+00       1.81541e+01       1.96e-03       1.00000e+00
   8         6.13753e+00       9.14770e+00       1.77e-04       1.00000e+00
   9         5.47036e+00       4.60960e+00       7.69e-05       1.00000e+00
  10         5.08686e+00       2.32441e+00       2.08e-05       1.00000e+00
  11         4.86639e+00       1.17121e+00       5.88e-06       1.00000e+00
  12         4.74866e+00       5.89345e-01       1.20e-06       1.00000e+00
  13         4.68964e+00       2.96133e-01       1.74e-07       1.00000e+00
  14         4.66139e+00       1.48698e-01       4.64e-08       1.00000e+00
  15         4.64756e+00       7.46674e-02       1.53e-08       1.00000e+00
  16         4.64054e+00       3.74768e-02       2.90e-09       1.00000e+00
  17         4.63699e+00       1.88017e-02       5.71e-10       1.00000e+00
  18         4.63521e+00       9.42917e-03       1.15e-10       1.00000e+00
  19         4.63431e+00       4.72735e-03       2.33e-11       1.00000e+00
  20         4.63386e+00       2.36933e-03       4.57e-12       1.00000e+00
  21         4.63363e+00       1.18708e-03       8.53e-13       1.00000e+00
  22         4.63352e+00       5.94528e-04       1.56e-13       1.00000e+00
  23         4.63346e+00       2.97654e-04       2.79e-14       1.00000e+00
  24         4.63343e+00       1.48973e-04       4.34e-15       1.00000e+00
  25         4.63342e+00       7.45356e-05       5.25e-16       1.00000e+00
  26         4.63341e+00       3.72823e-05       4.70e-17       1.00000e+00
  27         4.63341e+00       1.86450e-05       3.35e-18       1.00000e+00
  28         4.63340e+00       9.32350e-06       2.16e-19       1.00000e+00
  29         4.63340e+00       4.66200e-06       1.36e-20       1.00000e+00
  30         4.63340e+00       2.33106e-06       8.49e-22       1.00000e+00
  31         4.63340e+00       1.16554e-06       5.30e-23       1.00000e+00
  32         4.63340e+00       5.82776e-07       3.35e-24       1.00000e+00
  33         4.63340e+00       2.91389e-07       2.17e-25       1.00000e+00
  34         4.63340e+00       1.45695e-07       1.26e-26       1.00000e+00
  35         4.63340e+00       7.28474e-08       1.16e-27       1.00000e+00
  36         4.63340e+00       3.64237e-08       2.81e-28       1.00000e+00
  37         4.63340e+00       1.82119e-08       6.49e-29       1.00000e+00
  38         4.63340e+00       9.10594e-09       2.81e-28       1.00000e+00
Solved
Problem succesfully solved.

Optimal Elmore delay for Amax = 50 is 102.8634.
Optimal wire widths are: 

w =

   10.0000
   10.0000
    8.1903
    6.3949
    4.9122
    3.6970
    2.6976
    1.8730
    1.2229
    1.0122

generating the tradeoff curve
Problem succesfully solved.
Problem succesfully solved.
Problem succesfully solved.
Problem succesfully solved.
Problem succesfully solved.
Problem succesfully solved.
Problem succesfully solved.
Problem succesfully solved.
Problem succesfully solved.
Problem succesfully solved.
Problem succesfully solved.
Problem succesfully solved.
Problem succesfully solved.
Problem succesfully solved.
Problem succesfully solved.
Problem succesfully solved.
Problem succesfully solved.
Problem succesfully solved.