cantilever

% Design of a cantilever beam (recursive formulation)
% Section 4.5.4, pp. 163-165 in Boyd & Vandenberghe "Convex Optimization"
% (a figure is generated)
%
% We have a segmented cantilever beam with N segments. Each segment
% has a unit length and variable width and height (rectangular profile).
% The goal is minimize the total volume of the beam, over all segment
% widths w_i and heights h_i, subject to constraints on aspect ratios,
% maximum allowable stress in the material, vertical deflection y, etc.
%
% The problem can be posed as a geometric program (posynomial form)
%     minimize   sum( w_i* h_i)
%         s.t.   w_min <= w_i <= w_max,       for all i = 1,...,N
%                h_min <= h_i <= h_max
%                S_min <= h_i/w_i <= S_max
%                6*i*F/(w_i*h_i^2) <= sigma_max
%                y_1 <= y_max
%
% with variables w_i and h_i (i = 1,...,N).
% For other definitions consult the book.
% (See exercise 4.31 for a non-recursive formulation.)
%
% Almir Mutapcic 01/25/06

% optimization variables
N = 8;
gpvar w(N) h(N);

% constants
wmin = .1; wmax = 100;
hmin = .1; hmax = 6;
Smin = 1/5; Smax = 5;
sigma_max = 1;
ymax = 10;
E = 1; F = 1;

% objective is the total volume of the beam
% obj = sum of (widths*heights*lengths) over each section
% (recall that the length of each segment is set to be 1)
obj = w'*h;

% recursive formulation
v = posynomial; y = posynomial; % create empty posynomials
v(N+1,1) = 0; y(N+1,1) = 0;
for i = N:-1:1
  disp(['Processing recursion number: ' num2str(i)])
  v(i) = 12*(i-1/2)*F/(E*w(i)*h(i)^3) + v(i+1);
  y(i) = 6*(i-1/3)*F/(E*w(i)*h(i)^3)  + v(i+1) + y(i+1);
end

% constraint set
constr = [ ...
  wmin*ones(N,1) <= w; w <= wmax*ones(N,1);
  hmin*ones(N,1) <= h; h <= hmax*ones(N,1);
  Smin*ones(N,1) <= h./w; h./w <= Smax*ones(N,1);
  6*F*[1:N]'./(w.*(h.^2)) <= sigma_max*ones(N,1);
  y(1) <= ymax;
];

% solve GP and compute the optimal volume
[obj_value, solution, status] = gpsolve(obj, constr);
assign(solution);

% display results
disp('The optimal widths and heights are: ');
w, h
fprintf(1,'The optimal minimum volume of the beam is %3.4f\n', sum(w.*h))

% plot the 3D model of the optimal cantilever beam
close all;
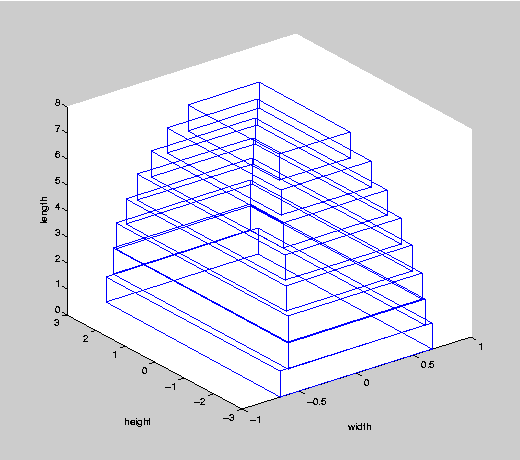
plot_cbeam([h; w])

Processing recursion number: 8
Processing recursion number: 7
Processing recursion number: 6
Processing recursion number: 5
Processing recursion number: 4
Processing recursion number: 3
Processing recursion number: 2
Processing recursion number: 1
 
Iteration     primal obj.         gap        dual residual     previous step.
 
   1         6.32203e+00       8.90000e+01       8.11e+01               Inf
   2         8.78270e+00       3.68726e+01       1.31e+00       8.71837e-01
   3         8.30332e+00       2.43097e+01       1.71e-01       6.39833e-01
   4         6.65830e+00       1.65548e+01       2.28e-02       6.33721e-01
   5         3.58991e+00       8.42655e+00       4.12e-05       1.00000e+00
   6         9.85278e-01       4.21177e+00       2.46e-06       1.00000e+00
   7        -8.50599e-02       2.10590e+00       1.02e-06       1.00000e+00
 
Iteration     primal obj.         gap        dual residual     previous step.
 
   1         5.41567e+00       8.90000e+01       7.55e-02               Inf
   2         5.37503e+00       4.44898e+01       1.09e-04       1.00000e+00
   3         5.28128e+00       2.22449e+01       1.11e-05       1.00000e+00
   4         5.10038e+00       1.11225e+01       2.97e-06       1.00000e+00
   5         4.79906e+00       5.56139e+00       6.92e-07       1.00000e+00
   6         4.40500e+00       2.78098e+00       1.21e-06       1.00000e+00
   7         4.05822e+00       1.39117e+00       7.54e-07       1.00000e+00
   8         3.87590e+00       6.96796e-01       7.89e-08       1.00000e+00
   9         3.80110e+00       3.48948e-01       5.22e-07       1.00000e+00
  10         3.77203e+00       1.74696e-01       7.80e-07       1.00000e+00
  11         3.75986e+00       8.74931e-02       7.82e-07       1.00000e+00
  12         3.75343e+00       4.38768e-02       1.85e-07       1.00000e+00
  13         3.75026e+00       2.20076e-02       2.15e-08       1.00000e+00
  14         3.74869e+00       1.10345e-02       2.79e-09       1.00000e+00
  15         3.74788e+00       5.52969e-03       3.95e-10       1.00000e+00
  16         3.74747e+00       2.76925e-03       5.04e-11       1.00000e+00
  17         3.74727e+00       1.38599e-03       4.95e-12       1.00000e+00
  18         3.74717e+00       6.93370e-04       3.81e-13       1.00000e+00
  19         3.74712e+00       3.46781e-04       2.53e-14       1.00000e+00
  20         3.74709e+00       1.73415e-04       1.60e-15       1.00000e+00
  21         3.74708e+00       8.67135e-05       1.01e-16       1.00000e+00
  22         3.74707e+00       4.33583e-05       6.29e-18       1.00000e+00
  23         3.74707e+00       2.16795e-05       3.94e-19       1.00000e+00
  24         3.74707e+00       1.08398e-05       2.46e-20       1.00000e+00
  25         3.74707e+00       5.41995e-06       1.54e-21       1.00000e+00
  26         3.74707e+00       2.70998e-06       9.61e-23       1.00000e+00
  27         3.74707e+00       1.35499e-06       6.01e-24       1.00000e+00
  28         3.74707e+00       6.77496e-07       3.75e-25       1.00000e+00
  29         3.74707e+00       3.38748e-07       2.36e-26       1.00000e+00
  30         3.74707e+00       1.69374e-07       1.49e-27       1.00000e+00
  31         3.74707e+00       8.46870e-08       9.28e-29       1.00000e+00
  32         3.74707e+00       4.23435e-08       6.37e-30       1.00000e+00
  33         3.74707e+00       2.11718e-08       1.90e-30       1.00000e+00
  34         3.74707e+00       1.05859e-08       8.96e-31       1.00000e+00
  35         3.74707e+00       5.29294e-09       4.31e-31       1.00000e+00
Solved
Problem succesfully solved.
The optimal widths and heights are: 

w =

    0.6214
    0.7830
    0.9060
    1.0124
    1.1004
    1.1762
    1.2000
    1.3333


h =

    3.1072
    3.9149
    4.5298
    5.0620
    5.5019
    5.8812
    6.0000
    6.0000

The optimal minimum volume of the beam is 42.3965