basic_odp

% Optimal doping profile optimization via GP
% (a figure is generated).
%
% This is an example taken directly from the paper:
%
%   Optimal Doping Profiles via Geometric Programming,
%   IEEE Transactions on Electron Devices, December, 2005,
%   by S. Joshi, S. Boyd, and R. Dutton.
%   (see pages 3-8 for problem details)
%
% Determines the optimal doping profile that minimizes base transit
% time in a (homojunction) bipolar junction transistor.
% This problem can be posed as a GP:
%
%   minimize   tau_B
%       s.t.   Nmin <= v <= Nmax
%              y_(i+1) + v_i^const1 <= y_i
%              w_(i+1) + v_i^const2 <= w_i, etc...
%
% where variables are v_i, y_i, and w_i.
%
% Almir Mutapcic and Siddharth Joshi 10/05
clear all;

% discretization size
M = 100;
% M = 1000; % takes a few minutes to process constraints

% problem constants
g1 = 0.42;
g2 = 0.69;
Nmax = 5*10^18;
Nmin = 5*10^16;
Nref = 10^17;
Dn0 = 20.72;
ni0= 1.4*(10^10);
WB = 10^(-5);
C =  WB^2/((M^2)*(Nref^g1)*Dn0);

% exponent powers
pwi = g2 -1;
pwj = 1+g1-g2;

% optimization variables
gpvar v(M) y(M) w(M)

% problem constraints
constr = [ Nmin*ones(M,1) <= v; v <= Nmax*ones(M,1); ];

for i = 1:M-1
  if( mod(i,100) == 0 ), disp(i), end;
  constr(end+1) = y(i+1) + v(i)^pwj <= y(i);
  constr(end+1) = w(i+1) + y(i)*v(i)^pwi <= w(i);
end

constr(end+1) = y(M) == v(M)^pwj;
constr(end+1) = w(M) == y(M)*v(M)^pwi;

% objective function is the base transmit time
tau_B = C*w(1);

% solve the optimal doping profile problem
[opt_val sol status] = gpsolve(tau_B, constr);
assign(sol);

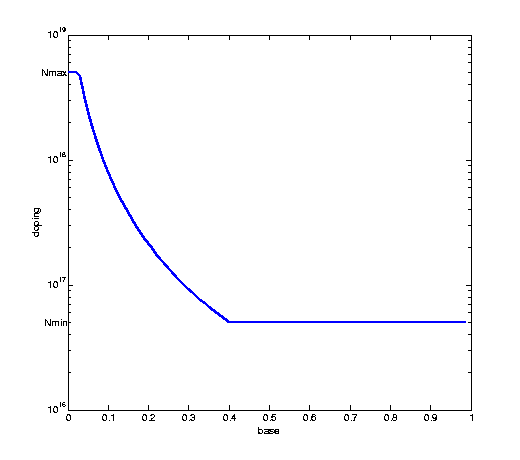
% plot the basic optimal doping profile
nbw = 0:1/M:1-1/M;
semilogy(nbw,v,'LineWidth',2);
axis([0 1 1e16 1e19]);
xlabel('base');
ylabel('doping');
text(0,Nmin,'Nmin ', 'HorizontalAlignment','right');
text(0,Nmax,'Nmax ', 'HorizontalAlignment','right');

 
Iteration     primal obj.         gap        dual residual     previous step.
 
   1         3.94508e+01       9.98000e+02       1.17e+04               Inf
   2         5.80827e+01       3.05279e+02       7.37e+00       9.74859e-01
   3         6.61589e+01       1.82296e+02       4.99e-01       7.39855e-01
   4         3.26923e+01       8.57134e+01       2.32e-04       1.00000e+00
   5         1.52941e+01       4.27124e+01       3.47e-06       1.00000e+00
   6         7.18683e+00       2.13540e+01       2.24e-06       1.00000e+00
   7         2.90726e+00       1.06433e+01       1.33e-06       1.00000e+00
   8         8.00136e-01       5.24929e+00       1.14e-06       1.00000e+00
   9         1.54772e-01       3.90269e+00       8.24e-07       5.00000e-01
  10        -5.70885e-01       3.15398e+00       1.27e-06       5.00000e-01
 
Iteration     primal obj.         gap        dual residual     previous step.
 
   1         1.69008e+02       9.98000e+02       3.56e+00               Inf
   2         1.60257e+02       9.23828e+02       2.60e+00       1.45878e-01
   3         1.52642e+02       8.82952e+02       2.14e+00       9.47111e-02
   4         1.36812e+02       8.00666e+02       1.34e+00       2.07373e-01
   5         1.02307e+02       6.66526e+02       4.62e-01       4.14716e-01
   6         4.75481e+01       4.80086e+02       2.85e-03       1.00000e+00
   7         1.84753e+01       2.40024e+02       9.21e-04       1.00000e+00
   8        -5.55470e+00       1.20106e+02       1.25e-03       1.00000e+00
   9        -1.65821e+01       6.02149e+01       4.56e-04       1.00000e+00
  10        -2.16678e+01       3.02677e+01       2.95e-04       1.00000e+00
  11        -2.41022e+01       1.52747e+01       1.07e-04       1.00000e+00
  12        -2.54356e+01       7.72753e+00       3.98e-05       1.00000e+00
  13        -2.62277e+01       3.90732e+00       9.77e-06       1.00000e+00
  14        -2.66904e+01       1.96952e+00       2.17e-06       1.00000e+00
  15        -2.69387e+01       9.90301e-01       6.19e-07       1.00000e+00
  16        -2.70650e+01       4.97355e-01       1.72e-07       1.00000e+00
  17        -2.71289e+01       2.49569e-01       3.65e-08       1.00000e+00
  18        -2.71612e+01       1.25129e-01       5.84e-09       1.00000e+00
  19        -2.71775e+01       6.26916e-02       7.17e-10       1.00000e+00
  20        -2.71856e+01       3.13909e-02       7.23e-11       1.00000e+00
  21        -2.71897e+01       1.57113e-02       7.25e-12       1.00000e+00
  22        -2.71918e+01       7.86119e-03       9.08e-13       1.00000e+00
  23        -2.71928e+01       3.93254e-03       1.44e-13       1.00000e+00
  24        -2.71933e+01       1.96694e-03       2.69e-14       1.00000e+00
  25        -2.71936e+01       9.83705e-04       6.03e-15       1.00000e+00
  26        -2.71937e+01       4.91938e-04       1.58e-15       1.00000e+00
  27        -2.71938e+01       2.46003e-04       4.26e-16       1.00000e+00
  28        -2.71938e+01       1.23016e-04       1.13e-16       1.00000e+00
  29        -2.71938e+01       6.15150e-05       2.90e-17       1.00000e+00
  30        -2.71938e+01       3.07608e-05       7.31e-18       1.00000e+00
  31        -2.71938e+01       1.53819e-05       1.79e-18       1.00000e+00
  32        -2.71938e+01       7.69173e-06       4.25e-19       1.00000e+00
  33        -2.71938e+01       3.84622e-06       9.42e-20       1.00000e+00
  34        -2.71938e+01       1.92326e-06       1.87e-20       1.00000e+00
  35        -2.71938e+01       9.61695e-07       3.06e-21       1.00000e+00
  36        -2.71938e+01       4.80870e-07       3.82e-22       1.00000e+00
  37        -2.71938e+01       2.40442e-07       3.43e-23       1.00000e+00
  38        -2.71938e+01       1.20223e-07       2.54e-24       1.00000e+00
  39        -2.71938e+01       6.01118e-08       2.48e-25       1.00000e+00
  40        -2.71938e+01       3.00560e-08       6.92e-26       1.00000e+00
  41        -2.71938e+01       1.50280e-08       8.43e-26       1.00000e+00
  42        -2.71938e+01       7.51402e-09       9.64e-26       1.00000e+00
Solved
Problem succesfully solved.