Slide 1

Today - interpreter, math int/float, style, black box examples, boolean logic, string introduction, string +=, string for/i/range loop

Slide 2

The Python Interpreter

Examples below use the Python interpreter >>> to type expressions into Python, see what they do. You can access the interpreter using the Hack Mode button on the experimental server, or within PyCharm, the "Python Console" tab at the lower left.

In the interpreter, you type code at the >>> prompt, Python evaluates it, printing any result on the next line.

>>> 1 + 1
2
>>>

You will learn many parts of Python by seeing those feature explained in class. For some cases, you can also learn what Python does by typing an example into the interpreter to see what it does. This is a nice technique in lecture to show what various Python features do.

For more details, see the guide Python Interpreter

Slide 3

Two Math Systems - int and float

You would think computer code has a lot to do with numbers, and here we are.

See in Python reference: Python Math

Surprisingly, computer code generally uses two different types of numbers - "int" and "float".

Slide 4

int numbers

The formal type "int" stores an integer
e.g. 5, 23, -6
There is no decimal-point dot in an int
e.g. 3.14 is not an int
int mathematics is precise and repeatable
3 + 4 is exactly 7
5 + 2 is also exactly 7
Math with int inputs .. produces int results
Except with division /

>>> 1 + 2
3
>>>

Slide 5

Use of ints - Indexing

"Indexing" is accessing an element inside something
Ints are naturally used for indexing
e.g. image.get_pixel(x, y)
x y numbers like 0 1 2 ..
There is no pixel at x = 2.5
Using a float here raises an error

Slide 6

float numbers

float 3.14, 1.2e23
float has a dot "." when printed
Surprisingly, float is not totally precise (later topic)
A float value in a computation forces the whole thing float
Even if the answer comes out even, a float input makes a float output

>>> 1.5 + 1.5
3.0
>>> 
>>> 1.0 + 2.0
3.0
>>> 

You do have to be careful with floats, particularly when comparing them:

>>> 0.1 + 0.2 == 0.3
False
>>> 0.1 + 0.2
0.30000000000000004
>>> 0.3

What is going on here?? This is something you will cover if you eventually take CS107!

Slide 7

Math Operators: + - * / **

int and float support the usual operators + - * /
Extra operator: ** is exponentiation
Precedence: * / go before + -
Otherwise evaluation goes left-right
Fine to add parenthesis to force the order you want
int-inputs → int-outputs, except / below
Python int values do not have a fixed "max"
Most languages have an int max
Interpreter: use the up-arrow to edit previous lines - pro tip!

>>> 2 + 3
5
>>> 2 + 3 * 4   # Precedence
14
>>> 2 * (1 + 2) # Use parenthesis
6
>>> 10 ** 2     # 10 Squared
100
>>> 2 ** 100    # Grains of sand in universe
1267650600228229401496703205376
>>>
>>>
>>> 1 + 2 + 3
6
>>> 1 + 2.0 + 3  # Makes result float
6.0

Slide 8

Division / → float

Division is tricky
a / b returns a float value always
Even if the division comes out even
What if we want an int?

>>> 7 / 2
3.5
>>> 8 / 2
4.0

Slide 9

Int Division // → int

This is a good idea from Python -
Have a formal "does int division operator"
a // b int division operator
Rounds answer down to an integer, aka discards the remainder
int inputs, always produces int output
e.g. Compute width of a half sized image: image.width // 2
Say image.width is 101
Want half size width of 50 pixels, not 50.5
We'll mention // again later when we need to use it

>>> 7 // 2
3
>>> 8 // 2
4
>>> 102 // 4
25

Slide 10

Big Picture Strategy - Divide and Conquer

Q: What is the main technique for solving big problems?
A: Divide and Conquer
Divide the big program into functions
Work on one function at a time
aka decomposition
As we build up CS techniques ...
Many techniques are in service of the big-picture goal

Slide 11

Data Flow Picture

Here is a way of looking at a program.

You have some files with data in them. You write code to lode the data into Python in one form. Then compute a transform into another form. Then a further computation produces an "answer" form. You publish the answer and get tweets of praise - the coding lifecycle! You can think of this as a sort of "data flow", from the original data to the final output.

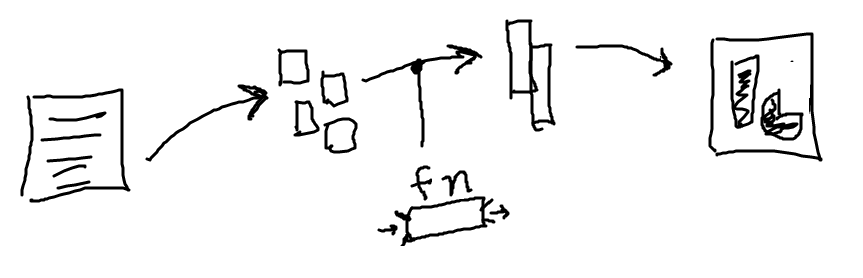
data flows through program

Slide 12

Today: Black Box Function

We have seen functions thus far, mainly we call them to run their code
Today we will start using functions as data flow
Each function is like a little box of some computation, with data-in and data-out
One stage in the picture above might be one function

Slide 13

"Black Box" Function Model

function is black box with parameters in and result
out

Black-box model of a function: function runs with parameters as input, returns a value. All the complexity of its code is sealed inside.

The black box model makes it easy to call the function - provide data you have as the input, call the function, get back an answer.

Slide 14

Strategy - One Function at a Time

For Divide and Conquer, want to be able to work on each function separately, one at a time. We need to keep the functions sealed off from each other as much as possible. The black box model works well for this, narrowing the interactions to just the input and output data for each function.

Slide 15

Write Black Box Code - Cases

Here we'll work through the code for first black-box examples. There are in the logic 1 section on the experimental server.

Think of each input as a "case" the function must handle, return the correct output. To be correct, code needs to handle all the possible input cases. One hallmark of putting something on the computer is that it forces you to think through all the cases.

Slide 16

1. winnings1() Example

> winnings1()

This is a first, simple example
Say we are writing a function for a lottery game
Rules: input is an int score 0..10 inclusive
score 5 or more, winnings is score * 12
score 4 or less, winnings is score * 10
We could make a table showing output for each input
Code needs to work for all cases, i.e. "general"
Later: we'll see how to put in formal tests that the code is getting the right output for each input

score winnings
    0
    10
    20
    30
    40
    60  # 12x kicks in here
    72
    84
    96
    108
   120

Slide 17

1. Function Input = Parameter

def winnings1(score):
    ...

The parameters to a function are its inputs
Left side of black-box picture
e.g. score is the input here
Each is like a variable with a value in it
Who put the value in the parameter?
The code that called this function
Code inside the function assume the parameter is set properly

Slide 18

2. Function Output = `return score * 10`

def winnings1(score):
    return score * 10

When a return line runs in a function
1. It exits the run of the function immediately
2. It specifies the return value that will go back to the caller
So the return statement determines the output of the function

Slide 19

Experiment 1 - winnings1()

You can type these in and hit the Run button as we go. The results are pretty easy to follow.

def winnings1(score):
    return score * 10

Try 1 line for the function:
return score * 10
Look at the table of output
See the basic role of parameter/return
But this output is wrong half the time

Slide 20

Experimental Server Output Format

def winnings1(score):
    return score * 12

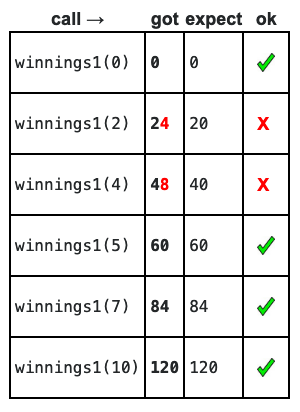
alt: experimental server output
table

Run function on experimental server, generates table of outputs
It calls the function many times, shows the results one per row
First "call" column is the input
Second "got" column is what the function returned
Easy to see the function's behavior this way

Slide 21

if-return Pick-Off Strategy

The function needs to handle all possible input cases
If-logic detects one case
Returns the answer for that case
Exiting the function
Lines below have if-return logic for other cases
Code is "picking off" the cases one by one
As we get past if-checks .. input must be a remaining case
Analogy: coin sorting machine
Coin rolls past holes, smallest to largest
1st hole dime, 2nd hole penny, 3rd nickel, 4th quarter
A dime never makes it to the quarter-hole
The dime is picked-off earlier

Slide 22

Experiment 2

def winnings1(score):
    if score >= 5:
        return score * 12

Add if-logic to pick off the >= 5 case. It's only right half the time.

Slide 23

`None` Result

None is the default return value of a function
None is returned if there is no explicit return value
Possibly by "falling off the end" of the function
All its lines have run and the function is finished
Above example, we see None if score < 5
If you see None like this
Somehow your code is not explicitly returning a value

Slide 24

Experiment 3 - Very Close

def winnings1(score):
    if score >= 5:
        return score * 12

    if score < 5:
        return score * 10

Add pick-off code for the score < 5 case. This code returns the right result in all cases. There is just at tiny logical flaw.

Slide 25

Experiment 4 - Perfect

def winnings1(score):
    if score >= 5:
        return score * 12

    # If we get to this line, score < 5
    return score * 10

Each pick-off recognizes a case and exits the function
Therefore for lines below, the picked-off case is excluded
That is, the score < 5 test is unnecessary
Coding strategy - helps your one-at-a-time attention
Work on code for case-1
When that's done, put it out of mind
Work on case-2, knowing case-1 is out of the picture

Slide 26

winnings1() Observations

Thinking about cases, if-logic to pick them off one at a time
Try changing <= to <
A form of Off By One bug - be careful right at the boundary
What about this form...

def winnings1(score):
    if score >= 5:
        return score * 12
        return score * 10

That does not work. The second return is in the control of the if. It never runs because the line above exits the function. In Python code, where a line is indented is very significant.

Slide 27

2. Winnings2 Example

Extra practice example.

> winnings2()

Say there are 3 cases. Use a series of if-return to pick them off. Need to think about the order. Need to put the == 10 case early.

Winnings2: The int score number in the range 0..10 inclusive. Bonus! if score is 10 exactly, winnings is score * 15. If score is between 4 and 9 inclusive, winnings is score * 12. if score is 3 or less, winnings is score * 10. Given int score, compute and return the winnings.

Solution

def winnings2(score):
    if score == 10:
        return score * 15
  
    if score >= 4:  # score <= 9 is implicit
        return score * 12
    
    # All score >= 4 cases have been picked off.
    # so score < 4 here.
    return score * 10

Slide 28

Boolean Values

For more detail, see guide Python Boolean

"boolean" value in code - True or False
if-test and while-test work with boolean inputs
e.g. bit.front_clear() returns a boolean
So we have if bit.front_clear():

Slide 29

Ways to Get a Boolean

== operator to compare two things
2 == 1 + 1 returns True
Two equal signs
Since single = is used for var assignment
!= - not-equal test
2 != 10 returns True
Compare greater-than / less-than
< is strict less-than
<= is less-or-equal to
These all work with ints, floats, other types of data

Try this in the interpreter (or Hack Mode button at bottom experimental server)

>>> n = 5   # assign to n to start
>>> n == 6
False
>>> n == 5
True
>>> n != 6
True
>>> 
>>> n < 10
True
>>> n < 5  # < is strict
False
>>> 
>>> n <= 5  # less-or-equal
True
>>> 
>>> n > 0
True

Slide 30

Boolean Operators: `and or not`

An operator combines values, returning a new value
e.g. + operator, 1 + 2 returns 3
Boolean operators combine True False values
Boolean operators: and or not
Suppose here that xxx and yyy are boolean values
xxx and yyy - if both sides are True, then it is True
aka all the inputs must be True
xxx or yyy - if either side or both sides are True, it is True
aka some input must be True
not xxx = inverts True/False
Why does not go to the left?
It's like the - for a negative number
e.g. -6

Slide 31

Weather Examples - `and or not`

Say we have temp variable is a temperature, and is_raining is a Boolean indicating if it's raining or not. Here are some examples to demonstrate and or not:

# OR: either or both are true
# Say we don't want to go outside if
# if it's cold or raining.
if temp < 50 or is_raining:
    print('not going outside!')


# AND
# We want to go outside if it's snowing.
if temp < 32 and is_raining:
    print('yay snow!')


# AND + NOT
# Sunny and nice case:
if temp > 70 and not is_raining:
    print('Sunny and nice!')


# Style note: don't use == False or == True
# to form a test. See above how "is_raining"
# is used directly in the test, or with a "not"
# in front of it.

Slide 32

Numeric `and` Example

Suppose we have this code, and n holds an int value.

if n > 0 and n < 10:
   # get here if test is True

What must n be inside the if-statement? Try values like 0 1 2 3 . 8 9 10

You can work out that n must be a an int value in the range 1..9 inclusive.

Slide 33

3. is_teen(n) Example

> is_teen()

is_teen(n): Given an int n which is 0 or more. Return True if n is a "teenager", in the range 13..19 inclusive. Otherwise return False. Write a boolean test to pick off the teenager case.