Mixed Linear System Estimation and Identification

Signal Processing, 90(3):966-971, March 2010. Shorter version in Proceedings IEEE Conference on Decision and Control, December 2009.

• mixed_system_est.pdf

We consider a mixed linear system model, with both continuous and discrete inputs and outputs, described by a coefficient matrix and a set of noise variances. When the discrete inputs and outputs are absent, the model reduces to the usual noise-corrupted linear system. With discrete inputs only, the model has been used in fault estimation, and with discrete outputs only, the system reduces to a probit model. We consider two fundamental problems: Estimating the model input, given the model parameters and the model output; and identifying the model parameters, given a training set of input-output pairs. The estimation problem leads to a mixed Boolean-convex optimization problem, which can be solved exactly when the number of discrete variables is small enough. In other cases the estimation problem can be solved approximately, by solving a convex relaxation, rounding, and possibly, carrying out a local optimization step. The identification problem is convex and so can be exactly solved. Adding 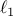regularization to the identification problem allows us to trade off model fit and model parsimony. We illustrate the identification and estimation methods with a numerical example.