Stochastic Matrix-Free Equilibration
Journal of Optimization Theory and Applications, 172(2), 436-454, 2017.
We present a novel method for approximately equilibrating
a matrix  using only multiplication by
using only multiplication by 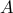 and
and 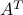 .
Our method is based on convex optimization and projected stochastic
gradient descent, using an unbiased estimate of a gradient
obtained by a randomized method.
Our method provably converges in expectation with an
.
Our method is based on convex optimization and projected stochastic
gradient descent, using an unbiased estimate of a gradient
obtained by a randomized method.
Our method provably converges in expectation with an 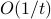 convergence rate and empirically gets good results with a small
number of iterations.
We show how the method can be applied as a preconditioner for
matrix-free iterative algorithms such as LSQR and Chambolle-Cremers-Pock,
substantially reducing the iterations required to reach a given level
of precision.
We also derive a novel connection between equilibration and
condition number, showing that equilibration minimizes an upper bound
on the condition number over all choices of row and column
scalings.
convergence rate and empirically gets good results with a small
number of iterations.
We show how the method can be applied as a preconditioner for
matrix-free iterative algorithms such as LSQR and Chambolle-Cremers-Pock,
substantially reducing the iterations required to reach a given level
of precision.
We also derive a novel connection between equilibration and
condition number, showing that equilibration minimizes an upper bound
on the condition number over all choices of row and column
scalings.