Extensions of Gauss Quadrature via Linear Programming
Foundations of Computational Mathematics, 15(4):953–971, 2015.
Gauss quadrature is a well known method for estimating the integral
of a continuous function with respect to a given measure as a
weighted sum of the function evaluated at a set of node points.
Gauss quadrature is traditionally developed using orthogonal polynomials.
We show that Gauss quadrature can also be obtained
as the solution to an infinite dimensional linear program:
Minimize the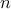 
th moment,
among all nonnegative measures that match the 0 through n-1
moments of the given measure.
While this infinite dimensional linear program provides no
computational advantage
in the traditional setting of integration on the real line,
it can be used to construct Gauss-like quadratures
in more general settings, including
arbitrary domains in multiple dimensions.