Techniques for exploring the suboptimal set
Optimization and Engineering, 11(2):319-337, June 2010.
The  -suboptimal set
-suboptimal set 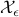 for an optimization problem is
the set of feasible points with objective value within
for an optimization problem is
the set of feasible points with objective value within  of optimal.
In this paper we describe some basic techniques for quantitatively
characterizing
of optimal.
In this paper we describe some basic techniques for quantitatively
characterizing 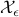 , for a given value of
, for a given value of  ,
when the original problem is convex,
by solving a modest number of related convex optimization problems.
We give methods for computing the bounding box of
,
when the original problem is convex,
by solving a modest number of related convex optimization problems.
We give methods for computing the bounding box of 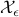 ,
estimating its diameter, and forming ellipsoidal approximations.
,
estimating its diameter, and forming ellipsoidal approximations.
Quantitative knowledge of 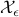 can be very useful
in applications.
In a design problem, where the objective function is some cost,
large
can be very useful
in applications.
In a design problem, where the objective function is some cost,
large 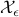 is good:
It means that there are many designs with nearly
minimum cost, and we can use this design freedom to improve a
secondary objective.
In an estimation problem,
where the objective function is some measure of plausibility,
large
is good:
It means that there are many designs with nearly
minimum cost, and we can use this design freedom to improve a
secondary objective.
In an estimation problem,
where the objective function is some measure of plausibility,
large 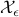 is bad: It means that quite different
parameter values are almost as plausible as the most plausible
parameter value.
is bad: It means that quite different
parameter values are almost as plausible as the most plausible
parameter value.