Confidence Bands for a Log-Concave Density
Journal of Computational and Graphical Statistics, 31:4, 1426–1438, 2022.
We present a new approach for inference about a log-concave distribution:
Instead of using the method of maximum likelihood, we propose to incorporate
the log-concavity constraint in an appropriate nonparametric confidence set for
the CDF 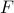 . This approach has the advantage that it automatically provides a
measure of statistical uncertainty and it thus overcomes a marked limitation of
the maximum likelihood estimate. In particular, we show how to construct
confidence bands for the density that have a finite sample guaranteed
confidence level. The nonparametric confidence set for
. This approach has the advantage that it automatically provides a
measure of statistical uncertainty and it thus overcomes a marked limitation of
the maximum likelihood estimate. In particular, we show how to construct
confidence bands for the density that have a finite sample guaranteed
confidence level. The nonparametric confidence set for 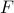 which we introduce
here has attractive computational and statistical properties: It allows to
bring modern tools from optimization to bear on this problem via difference of
convex programming, and it results in optimal statistical inference. We show
that the width of the resulting confidence bands converges at nearly the
parametric
which we introduce
here has attractive computational and statistical properties: It allows to
bring modern tools from optimization to bear on this problem via difference of
convex programming, and it results in optimal statistical inference. We show
that the width of the resulting confidence bands converges at nearly the
parametric  rate when the log density is
rate when the log density is 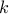 -affine.
-affine.