Block Splitting for Distributed Optimization
Mathematical Programming Computation, 6(1):77-102, 2014.
A shorter, preliminary version appeared as a
NIPS workshop paper.
This paper describes a general purpose method for solving convex optimization
problems in a distributed computing environment. In particular, if the problem
data includes a large linear operator or matrix 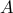 , the method allows for
handling each subblock of
, the method allows for
handling each subblock of 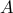 on a separate machine. The approach works as
follows. First, we define a canonical problem form called graph form, in
which we have two sets of variables
on a separate machine. The approach works as
follows. First, we define a canonical problem form called graph form, in
which we have two sets of variables 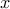 and
and 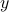 related by a linear operator
related by a linear operator
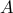 , such that the objective function is separable across these two sets of
variables. Many problems are easily expressed in graph form, including cone
programs and a wide variety of regularized loss minimization problems from
statistics, like logistic regression, the support vector machine, and the
lasso. Next, we describe graph projection splitting, a form of
Douglas-Rachford splitting or the alternating direction method of multipliers,
to solve graph form problems serially. Finally, we derive a distributed block
splitting algorithm based on graph projection splitting. In a statistical or
machine learning context, this allows for training models exactly with a huge
number of both training examples and features, such that each processor handles
only a subset of both. To the best of our knowledge, this is the only general
purpose method with this property. We present several numerical experiments in
both the serial and distributed settings.
, such that the objective function is separable across these two sets of
variables. Many problems are easily expressed in graph form, including cone
programs and a wide variety of regularized loss minimization problems from
statistics, like logistic regression, the support vector machine, and the
lasso. Next, we describe graph projection splitting, a form of
Douglas-Rachford splitting or the alternating direction method of multipliers,
to solve graph form problems serially. Finally, we derive a distributed block
splitting algorithm based on graph projection splitting. In a statistical or
machine learning context, this allows for training models exactly with a huge
number of both training examples and features, such that each processor handles
only a subset of both. To the best of our knowledge, this is the only general
purpose method with this property. We present several numerical experiments in
both the serial and distributed settings.