Engineers use mathematical "models" to evaluate, predict, and manage physical processes. On January 27, I sketched out a model of the flow process beneath a typical Feather River levee that was underlain by an old river channel. To make it simple, I broke down the physical system into several cells; for example, cell (1) is the channel on the river side of the levee. It gets water from the river and feeds it into the levee foundation, cell (2).

Each cell needs to be told something about itself; how permeable are its walls, how quickly does water flow through it, how much does it swell when pressurized. These define how fast a pressure wave will migrate through the foundation from the water to the land side of the levee.

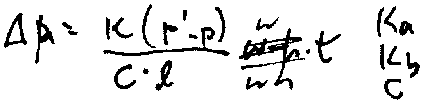
These factors can be combined into a set of differential equations, or, as I've done here, into a step-by-step finite difference model.

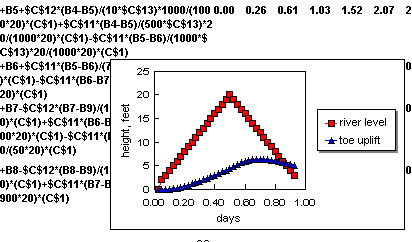
The model can be solved on an ordinary spreadsheet such as Lotus 1-2-3. Here are sample results. I assumed an imaginary river rise to 20 feet for a half day, then a drop for a half day.

You can see from the graph that the water pressure beneath the levee -- which can cause dangerous sand boils -- lags behind the river rise. The peak toe pressure occurs after the water has dropped. Hence, the most dangerous time can be after the peak of the flood.

In fact, this is just a rough sample calculation. Some of the data necessary to adequately confirm such a model were collected by the State Department of Water Resources in 1991, but never made public.

Other links:

Lance Williams' San Francisco Examiner lead article on levee failures, January 12, 1997

Some geological history of the failure area, leading to prediction of failure hot spots.

Some information on sand boils.

A helicopter inspection on January 17 Feather River flood hydrography Why levees may fail after the flood peak

Comparison with Pajaro River valley

Questions or Comments?

meehan@blume.stanford.edu; or call Dick Meehan at (415) 323-0525