Subgraph Frequencies

A companion webpage to the WWW 2013 paper by
Johan Ugander, Lars Backstrom, and Jon Kleinberg,
including code.

Introduction

In our upcoming paper Subgraph Frequencies: Mapping the Empirical and Extremal Geography of Large Graph Collections" (PDF), to appear in May 2013 at the 22nd ACM International World Wide Web Conference, we found that there are fundamental combinatorial constraints governing the frequency of subgraphs that constrain all graphs in previously undocumented ways. We also found that there are empirical properties of social graphs that relegate their subgraph frequencies to a seriously restricted subspace of the full feasible space. Together, we present two complementary frameworks that shed light on a fundamental question pertaining to social graphs:

What properties of social graphs are 'social' properties and
what properties are 'graph' properties?

We contribute two frameworks for analyzing this question: one characterizing extremal properties of all graphs and one characterizing empirical properties of social graphs. Together the two frameworks offer a direct contribution to one of the most well-known observations about social graphs: the tendency of social relationships to close triangles, and the relative infrequency of what is sometimes called the 'forbidden triad': three people with two social relationships between them, but one absent relationship. Our frameworks show that the frequency of this 'forbidden triad' is non-trivially restricted not just in social graphs, but in all graphs.

Harnessing our results more generally, we are in fact able to show that almost all $k$ node subgraphs have a frequency that is non-trivially bounded. Thus, there is an extent to which almost all subgraphs are mathematically 'forbidden' from occurring beyond a certain frequency.

What are subgraph frequencies?

Subgraph frequencies describe a graph by the frequencies with which all possible small subgraphs occur within it. More precisely, we choose a small number $k$ (e.g. $k = 3$ or $4$); then, for a graph $G$, we create a vector with a coordinate for each distinct $k$-node subgraph $H$, specifying the fraction of $k$-tuples of nodes in $G$ that induce a copy of $H$ (in other words, the frequency of $H$ as an induced subgraph of $G$).

Let $s(H,G)$ denote the subgraph frequency of $H$ in $G$. We can also equivalently define the subgraph frequency $s(H,G)$ as the probability that a random $k$-node subset of nodes in $G$ induces a copy of $H$. For $k=3$, these descriptions correspond to what is sometimes referred to as the triad census.

For $k=3$ and $k=4$, here is what all the undirected subgraphs look like (there are 4 three-node graphs and 11 four-node graphs):


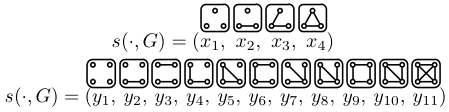
The orders presented here are also the orders used in the discussion below.

So what do subgraph frequencies look like empirically?

This work was done in collaboration with Facebook (while the first author was visiting Facebook through their internship program), making it possible to see what a really large collection of graphs look like on a detailed subgraph level. We extracted three different collections of social graphs from Facebook: neighborhoods, groups and events. The collections are all induced graphs from the Facebook friendship graph, which records friendship connections as undirected edges between users, and thus all our induced graphs are also undirected.

We did not include edges formed by Facebook 'subscriptions' in our study, nor did we include Facebook 'pages' or connections from users to such pages. All Facebook social graph data was analyzed in an anonymous, aggregated form. We studied:

So where do these subgraph frequencies live empirically? Below is Figure 1 from our paper, showing the 3-node subgraph frequencies of the above collections consisting of 50, 100, and 200 nodes. Neighborhoods are orange, groups are green, and events are lavender:

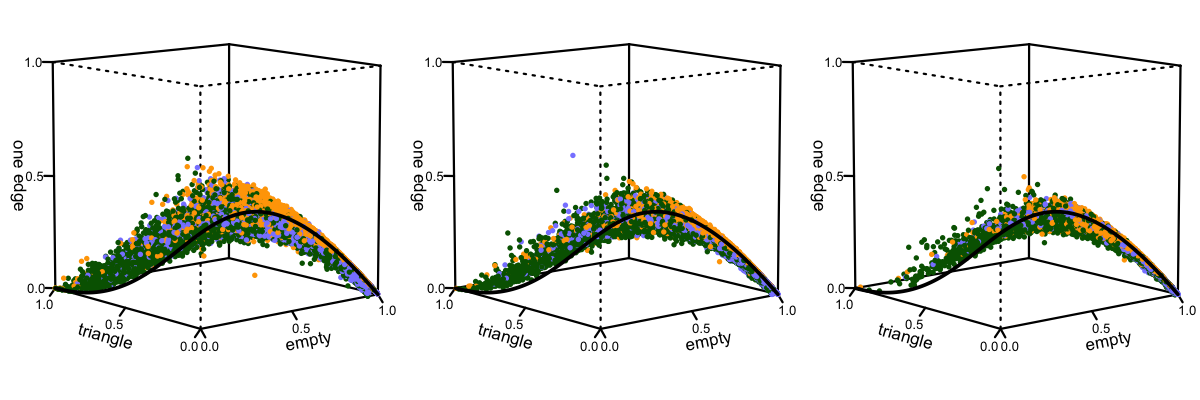
The black line corresponds to the expected frequencies for $G_{n,p}$, the Erdos-Renyi random graph family, as a function of edge density $p$. The paper contains more details, but the main point to notice for now is that these thousands of graphs are empirically concentrated to a very particular subspace of the simplex.

Is the entire simplex of frequencies feasible?

No! The frequencies of 3-node and 4-node subgraphs live in a 4-simplex and an 11-simplex, respectively. The frequencies of 3-node subgraphs for the social graphs shown above certainly don't fill the 4-simplex, and it turns out: there are fundamental constraints on what subgraph frequencies can look like that constrain all graphs, not just social graphs.

The constraints on the subgraph frequencies follow from what are known as 'graph homomorphism inequalities', which are fundamental combinatorial relationships that govern how subgraphs co-occur. It turns out that there are many combinations of subgraphs that are fundamentally infeasible.

To prove this infeasibility, we used several graph homomorphism inequalities (specifically: Kruskal-Katona, Moon-Moser, and the Sidorenko Tree Bound) and related the frequencies of all the subgraphs in a possible graph to the edge density of the graph. The edge density is really just the subgraph frequency of the two-node clique in the graph, and so we can relate other subgraph frequencies to it via homomorphism inequalities. This part of the work gets rather technical, and is outlined in the paper (PDF).

By sweeping over all edge densities, we found that the homomorphism inequalities we studied combine to restrict the abundancy of all subgraphs that are not empty and not complete graphs. Below is Figure 5 from our paper, where each x-axis is edge density, from 0.0 to 1.0, and the green boxes are the limits set by the combined homomorphism inequalities. The scattered dots are the frequencies of empirical 50-node graphs from Facebook.



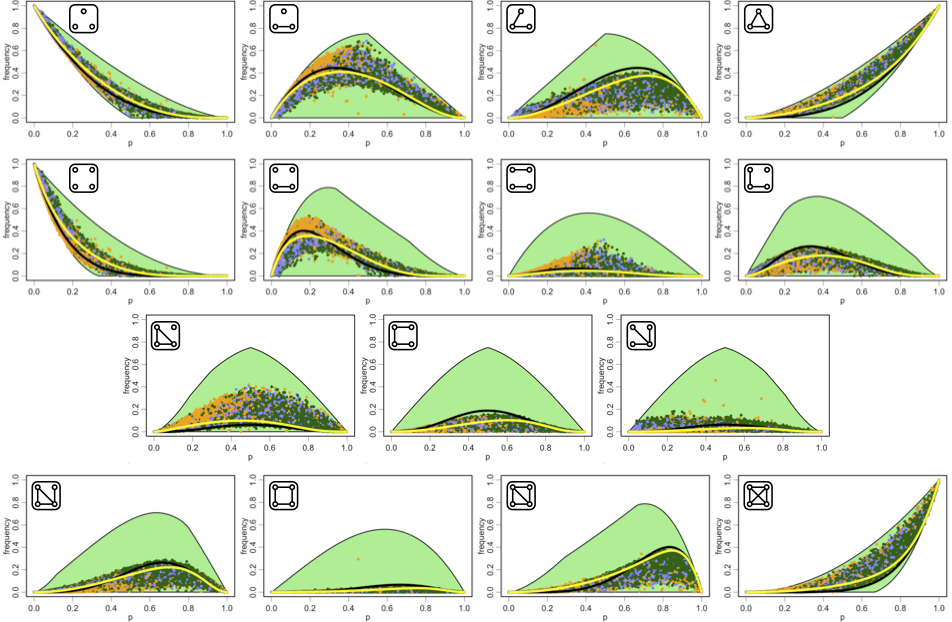
The black lines are again $G_{n,p}$ as a function of $p$, and we'll explain the yellow lines futher along (it's related to the empirical framework describe below). Notice here that the 'forbidden triad' can not occur with a frequency of more than 2/3 in any graph, not just social graphs. Notice that squares are also very rare by both combinatorial constraints and even more so empirically. While working on this paper, our working title for the work was actually "It's Hip to Be Square," but we ended up going for a more serious title, for better or worse.

None of the green boxes except those for the empty and complete subgraphs ever touch "1.0". As we prove formally in the paper (see Proposition 4.9) it turns out that no subgraph, other than the empty or complete subgraphs, can ever occur with 100% frequency in a large enough graph.

There are some details of the results that we're glossing over here: the green bounds are only outer bounds, and considering additional graph homomorphism inequalities may very well tighten the green boxes. We do however know that large tracts of the green space are inhabitable by graphs but no social graphs appear there. See the end of Section 4.3 for details.

For more on the theory of graph homomorphisms, see the excellent survey by Borgs, Chayes, Lovaz, Sos, and Vesztergombi on Counting Graph Homomorphisms (PDF) or the equally excellent broader survey by Lovasz on Very Large Graphs.

What more can we say about empirical social graphs?

When examining the two figures reproduced above, it should actually come as a surprise that $G_{n,p}$, the Erdos-Renyi random graph family, traces the empirical distribution of subgraphs so well. Recall that only a handful of properties of social networks are replicated well by simple Erdos-Renyi graphs. For example, they do have a small (logarithmic) diameter. But most important properties require more sophisticated models: clustering (Watts & Strogatz 1998) and navigability (Kleinberg 2000) being important examples.

Having noticed this close match between our subgraph frequency data and the expected behavior of the Erdos-Renyi model, we were able to design a concise random walk view of edge formation using the theory of Markov chains. The 'Edge Formation Random Walk' framework we developed starts out by reexamining $G_{n,p}$ on a subgraph level. With this new perspective, we are then able to easily tinker with the ways in which edges are formed. Specifically, we were able to extend our model away from merely describing $G_{n,p}$ by introducing an extra formation force caused by triadic closure, the tendency of people to be introduced by mutual acquaintances. Adding this force we were then able to ask: how does the equillibrium distribution of such a perturbed model compare to empirical social graphs? Here is the transition diagram of our markov chain on four-node graphs. It's very pretty:



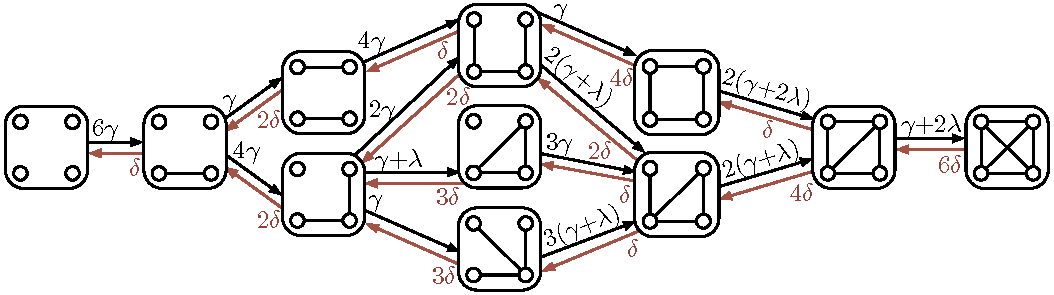
Fitting the parameters of this model to our datasets, it turns out that random edge formation plus solely triadic closure describes the subgraph frequencies of our graphs with remarkable accuracy. Here are the frequencies of the 4-node subgraphs of neighborhoods, taken from Figure 4, with a logarithmic y-axis:



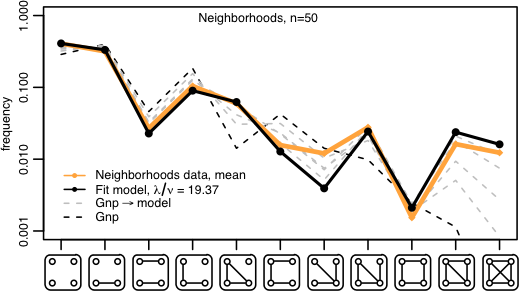
Looking at the above figure, first notice how good the fit is: the data is the orange line and the model is the black line. Next, notice again how rare squares are. We actually first observed this in our 2012 PNAS paper on 'Structural Diversity on Social Contagion', co-authored also with Cameron Marlow at Facebook, where squares were incredibly rare in the email dataset we were examining. This is clear from the large error bars on Figure 1(d) of that paper. The behavior of the fit model is also seen as the yellow lines in the earlier figure on extremal bounds.

The sole point of disagreement between the model and the data, the four node star, is likely explainable through higher order forces: triadic closure as a theory only effects triplets of individuals, and understanding the overabundance of four node stars can probably be understood by incorporating some model of larger group formation. But we haven't looked so closely at this.

We hope that our Edge Formation Random Walk model provides a useful framework for exploring subgraph frequencies not just in social graphs but also other graphs: other perturbations may give wildly different frequencies appropriate for describing other contexts very different from social networks.

A take-away lesson: Sometimes observations about social networks are observations about people, sometimes they're observations about graphs. Be careful distinguishing the two!

Finally, for a wonderful classic example of the importance of the question, "What is a property of people and what is a property of graphs?", see The Princeton Companion to Mathematics, Section IV.19 Extremal and Probabilistic Combinatorics (PDF here), which relates the story of the Hungarian sociologist Sandor Szalai and his accidental rediscovery of Ramsey Theory.

Is there code to play with?

Yes. We are releasing code written in R for computing the extremal bounds found in the paper, and also for solving for the equilibrium of the Edge Formation Random Walk model:

This script computes the subgraph frequency bounds described above, and helps illustrate how the different inequalities combine to form the extremal bounds. In particular, it can be instructive to modify the boolean variables such as 'bool_KruskalKatona' to turn the different inequalities on or off. This code requires the R package 'lpSolve' for solving Linear Programs.

The script also includes a solver of the Edge Formation Random Walk model for arbitrary values of $\lambda$, which are graphically overlaid on top of the bounds (along with $G_{n,p}$, which corresponds to $\lambda=0$).